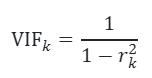A multicolinearidade é um problema que pode ocorrer em regressões quando duas ou mais variáveis independentes explicam o mesmo fenômeno. Como exemplo, imagine um modelo de regressão para precificar imóveis usando como variáveis a área e o número de cômodos.
Dessa forma, duas ou mais variáveis independentes altamente correlacionadas podem ser um um alerta de multicolinearidade, o que causa distorções no modelo estimado:
- Erros padrão maiores (menor eficiência e estimativas menos precisas);
- Estimadores sensíveis a pequenas variações dos dados;
- Dificuldade na separação dos efeitos de cada uma das variáveis.
A identificação do problema da multicolinearidade pode ser feita pelos seguintes testes estatísticos:
- Farrar & Glauber
- VIF (Variance Inflation Factor)
- Tolerance
No caso da estatística VIF, mais comumente utilizada, calculamos:
onde é o coeficiente de correlação da variável
com as demais variáveis.
Com o valor da estatística VIF em mãos, costuma-se utilizar as seguintes regras de bolso para identificar multicolinearidade:
- VIF <= 1: sem multicolinearidade;
- 1 < VIF < 10: multicolinearidade aceitável;
- VIF >= 10: multicolinearidade problemática.
Dessa forma, o VIF pode ser utilizado como critério de decisão para seleção de variáveis em modelos preditivos.
Exemplo em Python
Primeiro importamos as bibliotecas necessárias e uma tabela de séries temporais mensais:
| ipca | selic | cambio | pib_mensal | inpc | |
|---|---|---|---|---|---|
| data | |||||
| 2000-01-01 | 0.62 | 19.00 | 1.8037 | 92576.6 | 0.61 |
| 2000-02-01 | 0.13 | 19.00 | 1.7753 | 91770.4 | 0.05 |
| 2000-03-01 | 0.22 | 19.00 | 1.7420 | 92579.9 | 0.13 |
| 2000-04-01 | 0.42 | 18.50 | 1.7682 | 91376.2 | 0.09 |
| 2000-05-01 | 0.01 | 18.50 | 1.8279 | 98727.0 | -0.05 |
| ... | ... | ... | ... | ... | ... |
| 2023-12-01 | 0.56 | 12.25 | 4.8972 | 939618.2 | 0.55 |
| 2024-01-01 | 0.42 | 11.75 | 4.9144 | 883698.6 | 0.57 |
| 2024-02-01 | 0.83 | 11.25 | 4.9644 | 897934.3 | 0.81 |
| 2024-03-01 | 0.16 | 11.25 | 4.9801 | 972728.9 | 0.19 |
| 2024-04-01 | 0.38 | 10.75 | 5.1291 | 959465.9 | 0.37 |
292 rows × 5 columns
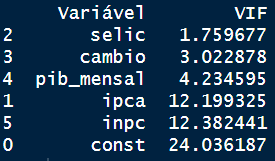
Agora calculamos o VIF:
| Variável | VIF | |
|---|---|---|
| 2 | selic | 1.759677 |
| 3 | cambio | 3.022878 |
| 4 | pib_mensal | 4.234595 |
| 1 | ipca | 12.199325 |
| 5 | inpc | 12.382441 |
| 0 | const | 24.036187 |
A tabela mostra as variáveis testadas e a estatística VIF. Note que variáveis “semelhantes”, como as taxas de inflação, apresentam estatísticas VIF elevadas, indicando multicolinearidade.
Conclusão
O VIF é uma estatística útil para identificar multicolinearidade em problemas de regressão. Neste artigo, mostramos seu cálculo, a interpretação e uma aplicação em Python.
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.