No post de hoje iremos construir um código em R para analisar o impulso resposta em séries financeiras, especificadamente a resposta do IBOVESPA a um choque de um desvio padrão na SELIC.
VAR e IRF
A função de impulso resposta (FIR) é utilizada para obter uma visão do comportamento dinâmico de um modelo. De maneira simplificada, utiliza-se um VAR para representar que cada variável em seu sistema possa ser explicada por sua média e pela soma de choques com pesos associados, sendo que cada peso representa os choques nas variáveis. Por meio de diversos métodos é possível usar tais pesos para computar o efeito de uma unidade de aumento de inovação da variável em determinado tempo sobre outra variável em um tempo futuro, mantendo todas as outras inovações e tempos constantes.
Variáveis
Como exemplo, criaremos um VAR definido de acordo com o trablaho de Nunes etl al. (2005), com algumas modificações. O objetivo é avaliar as inter-relações de variáveis macroeconomicas e financeiras através do uso de funções impulso resposta. As variáveis escolhidas são:
- EMBI+ Risco-Brasil
- Ibovespa - Índice de ações - Fechamento
- PIB mensal - Valores correntes
- Taxa de câmbio real bilateral - IPA-DI - BR/US
- Taxa de juros - Selic acumulada no mês anualizada base 252
- Índice Nacional de Preços ao Consumidor Amplo (IPCA)
Vamos utilizar os seguintes pacotes para criar o modelo VAR e avaliar o FIR.
library(magrittr) library(GetBCBData) library(ipeadatar) library(lubridate) library(tidyr) library(dplyr) library(tsibble) library(purrr) library(forecast) library(ggplot2) library(vars)
Coleta e Tratamento
Iremos coletar os dados de diferentes fontes, utilizando o código abaixo.
# |-- Coleta e pré tratamento --|
# PIB mensal - Valores correntes - R$ milhões (BCB)
# Taxa de juros - Selic acumulada no mês anualizada base 252 - % a.a.
# Índice Nacional de Preços ao Consumidor Amplo (IPCA) - % a.m.
df_bcb <- GetBCBData::gbcbd_get_series(
id = c(
"pib_mensal" = 4380,
"selic" = 4189,
"ipca" = 433
),
first.date = lubridate::ymd("2003-12-01"),
use.memoise = FALSE
) %>%
tidyr::pivot_wider(
id_cols = "ref.date",
names_from = "series.name",
values_from = "value"
) %>%
dplyr::rename("date" = "ref.date") %>%
dplyr::mutate(date = tsibble::yearmonth(.data$date))
# Taxa de câmbio real bilateral - IPA-DI - BR/US: índice (média 2010 = 100)
# Ibovespa - Índice de ações - Fechamento - Anbima - % a.m.
# EMBI+ Risco-Brasil - ponto-base
# Índice Nacional de Preços ao Consumidor Amplo (IPCA) - Índice (dez. 1993 = 100)
codes_ipea <- c(
"ibovespa" = "ANBIMA12_IBVSP12",
"cambio_real" = "GAC12_TCEREUA12",
"embi_br" = "JPM366_EMBI366",
"ipca_indice" = "PRECOS12_IPCA12"
)
df_ipea <- ipeadatar::ipeadata(codes_ipea) %>%
tidyr::pivot_wider(
id_cols = "date",
names_from = "code",
values_from = "value"
) %>%
dplyr::select("date", dplyr::all_of(codes_ipea)) %>%
dplyr::group_by(date = tsibble::yearmonth(.data$date)) %>%
dplyr::summarise(
dplyr::across(
.cols = !dplyr::any_of("date"),
.fns = ~mean(.x, na.rm = TRUE)
),
.groups = "drop"
)
# |-- Cruzar tabelas --|
df_fin_macro <- dplyr::left_join(
x = df_ipea,
y = df_bcb,
by = "date"
) %>%
dplyr::filter(lubridate::as_date(date) >= lubridate::ymd("2003-12-01")) %>%
tidyr::drop_na()
Deflacionaremos os dados do PIB mensal, do IBOVESPA e da SELIC.
# Deflacionamento ---------------------------------------------------------
# Deflacionar séries nominais (note que para a SELIC é mais apropriado a
# equação de Fisher, mas optamos por simplificar)
df_fin_macro %<>%
dplyr::mutate(
dplyr::across(
.cols = c("pib_mensal", "ibovespa", "selic"),
.fns = ~ipca_indice[date == dplyr::last(date)] / ipca_indice * .x
)
) %>%
dplyr::select(-"ipca_indice")
Estacionariedade e Diferenciação
Antes de construir o VAR, é necessário certificar que estamos utilizando variáveis estacionárias, para isso, usamos a função constituída abaixo para aplicar os testes ADF, KPSS e PP. Caso houver variáveis não estacionárias, realizaremos as suas respectivas diferenciações em seguida.
#' Report number of differences to make time series stationary (vectorized)
#'
#' @param x List-like object with vectors of the series to be tested
#' @param test Type of unit root test to use, see forecast::ndiffs
#' @param term Specification of the deterministic component in the regression, see forecast::ndiffs
#' @param alpha Level of the test, possible values range from 0.01 to 0.1
#' @param na_rm Remove NAs from x?
#'
#' @return Tibble with variable name from x and the number of differences found
#' @export
report_ndiffs <- function (
x,
test = c("kpss", "adf", "pp"),
term = c("level", "trend"),
alpha = 0.05,
na_rm = TRUE
) {
# All possible tests and terms
ndiffs_tests <- purrr::cross(list(test = test, type = term))
ndiffs_tests <- purrr::set_names(
x = ndiffs_tests,
nm = paste(
purrr::map_chr(ndiffs_tests, 1),
purrr::map_chr(ndiffs_tests, 2),
sep = "_"
)
)
# Nested for-loop
purrr::map(
.x = if (na_rm) {stats::na.omit(x)} else x,
.f = ~purrr::map(
.x = ndiffs_tests,
.f = function (y) {
forecast::ndiffs(
x = .x,
alpha = alpha,
test = y[[1]],
type = y[[2]]
)
}
)
) %>%
purrr::map_df(dplyr::bind_rows, .id = "variable") %>%
# Create column with most frequent value to differentiate
dplyr::rowwise() %>%
dplyr::mutate(
ndiffs = dplyr::c_across(!dplyr::any_of("variable")) %>%
table() %>%
sort(decreasing = TRUE) %>%
names() %>%
purrr::chuck(1) %>%
as.numeric()
) %>%
dplyr::ungroup()
}
Após a construção da função, a aplicamos nos dados e fazemos a diferenciação.
# Estacionariedade -------------------------------------------------------- # Testes (ADF, PP, KPSS) p/ obter nº de differenças p/ a série ser estacionária vars_ndiffs <- df_fin_macro %>% dplyr::select(-"date") %>% report_ndiffs() # Diferenciar séries para obter estacionariedade df_fin_macro %<>% dplyr::mutate( dplyr::across( .cols = vars_ndiffs$variable[vars_ndiffs$ndiffs > 0], .fns = ~tsibble::difference( x = .x, differences = vars_ndiffs$ndiffs[vars_ndiffs$variable == dplyr::cur_column()] ) ) ) %>% tidyr::drop_na()
Visualização das variáveis
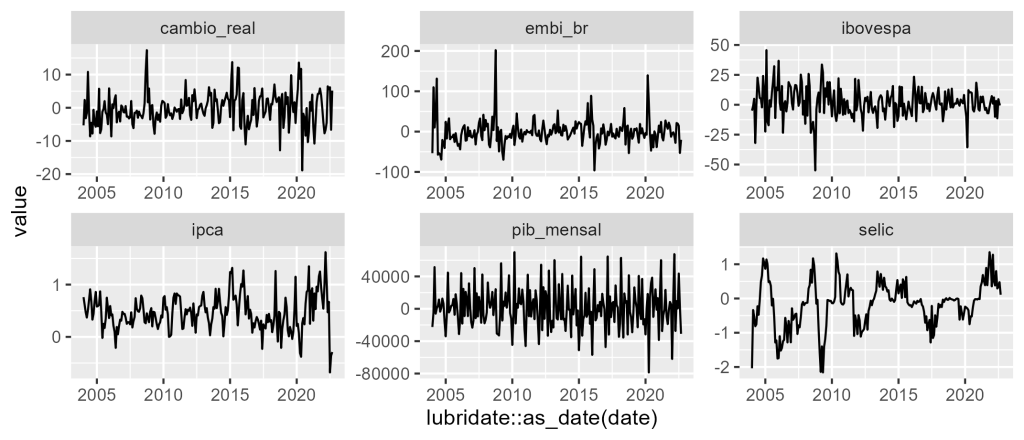
Com os dados tratados, visualizamos em um gráfico o resultado das séries.
# Visualização de dados --------------------------------------------------- # Gráfico de linhas da séries df_fin_macro %>% tidyr::pivot_longer(-"date") %>% ggplot2::ggplot() + ggplot2::aes(x = lubridate::as_date(date), y = value) + ggplot2::geom_line() + ggplot2::facet_wrap(~name, scales = "free")
Construindo o VAR
Para criar o modelo VAR, é possível realizar a seleção de defasagens por critérios de informação por meio da função VARselect do pacote {vars}. Com a quantidade defasagem definidas, é possível enfim estimar o modelo VAR com a função VAR do pacote {vars}.
# Seleção de defasagens VAR por critérios de informação lags_var <- vars::VARselect( y = df_fin_macro[-1], lag.max = 12, type = "const" ) # Estimar modelo VAR fit_var <- vars::VAR( y = df_fin_macro[-1], p = lags_var$selection["AIC(n)"], type = "const", lag.max = 12, ic = "AIC" )
Construindo o IRF
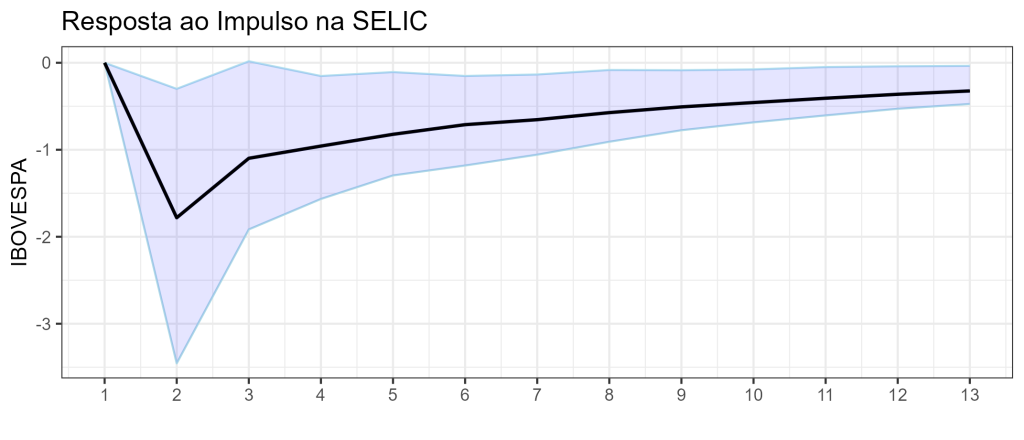
Com o resultado, avaliamos o impulso reposta por meio da função irf do pacote {vars} e averiguamos o resultado por meio de um gráfico. Avaliaremos um choque na SELIC e a resposta no IBOVESPA.
# Obter os coeficientes de impulso resposta do VAR
# Exemplo 1: choque na SELIC e resposta no IBOVESPA
irf_var <- vars::irf(
x = fit_var,
impulse = "selic",
response = "ibovespa",
n.ahead = 12
)
# Plotar gráfico de impulso resposta
lags = 1:13
df_irf <- data.frame(irf = irf_var$irf, lower = irf_var$Lower, upper = irf_var$Upper,
lags = lags)
colnames(df_irf) <- c('irf', 'lower', 'upper', 'lags')
number_ticks <- function(n) {function(limits) pretty(limits, n)}
ggplot(data = df_irf,aes(x=lags,y=irf)) +
geom_line(aes(y = upper), colour = 'lightblue2') +
geom_line(aes(y = lower), colour = 'lightblue')+
geom_line(aes(y = irf), size=.8)+
geom_ribbon(aes(x=lags, ymax=upper,
ymin=lower),
fill="blue", alpha=.1) +
xlab("") + ylab("IBOVESPA") +
ggtitle("Resposta ao Impulso na SELIC") +
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
plot.margin = unit(c(2,10,2,10), "mm"))+
geom_line(colour = 'black')+
scale_x_continuous(breaks=number_ticks(13))+
theme_bw()
Interpretação
Dado um choque de um desvio padrão na variável SELIC do modelo a variável IBOVESPA do modelo (retornos) diminuirá em cerca de 1,78 no primeiro período, dado que o coeficiente é significativo (intervalos de confiança fora do zero) ou seja, a interpretação é na mesma unidade da variável, como especificada no modelo... se o modelo estivesse especificado em log, a interpretação seria %.
________________________________________________
Quer se aprofundar no assunto?
Alunos da trilha de Ciência de dados para Economia e Finanças possuem acesso o curso Analise de dados Macroeconômicos e Financeiros e podem aprender a como construir projetos que envolvem dados reais usando modelos econométricos e de Machine Learning com o R.
________________________________________________
Referências
Nunes, M. S., da Costa Jr, N. C., & Meurer, R. (2005). A relação entre o mercado de ações e as variáveis macroeconômicas: uma análise econométrica para o Brasil. Revista Brasileira de Economia, 59(4), 585-607.