O objetivo do post de hoje será mostrar os fundamentos para a criação de uma Analise Exploratória de dados econômicos utilizando o Python.
Antes de começar a realizar a exploração de dados econômicas, é necessário entender os formatos das amostras que esses tipos de dados são encontrados. Em geral, possuem três formas:
- Corte Transversal: dados com amostras geralmente fixas em determinado período de tempo
- Série Temporal: coleção de observações de uma amostra feitas sequencialmente ao longo do tempo
- Dados em painel: informações de várias unidades amostrais (indivíduos, empresas, etc) acompanhadas, em geral, ao longo do tempo
Iremos lidar com dados econômicos em Série Temporal, devido ao fato de serem encontrados com maior abundância em bases de dados, bem como são os mais utilizado para análises, modelagem e previsões.
Série Temporal
Mas qual é o formato da um conjunto de dados em Série Temporal?
Uma Série Temporal é especificada por uma coluna representando os dados de uma respectiva variável (ou variáveis) e outra coluna (ou índice) representado a data, seja esta em frequência diária, semanal, mensal, trimestral, semestral ou anual.
Além disso, uma série temporal pode ser univariada ou multivariada. Uma Série Temporal univariada é representada por apenas uma variável, já a multivariada é representada por duas ou mais variáveis. Esse ponto é de grande importância ao realizar uma analise exploratória.
Análise Exploratória de Dados (AED)
Mas além do formato dos dados, o que é Análise Exploratória?
A AED é um conjunto de métodos que o analista utiliza para descrever um determinado conjunto de dados, permitindo compreender o comportamento de diversas variáveis. Permite também solidificar uma base para criar hipóteses e modelos preditivos/causais.
Em relação a Série Temporal, é importante saber que são tipos de dados que possuem características únicas, portanto, é necessário entender alguns pontos, tanto por questões de análise, quanto também por questões de modelagem.
- Sazonalidade;
- Tendencia;
- Autocorrelação;
- Estacionariedade.
Esses pontos podem ser analisados por meio de estatísticas e gráficos, entre eles
- Média, mediana, desvio padrão e IQR;
- Gráfico de histograma;
- Gráfico de linha;
- Gráfico de sazonalidade;
- Correlogramas ACF e PACF;
-
Testes de estacionariedade ADF, KPSS e PP.
Existem diversas outras características, bem como diversas ferramentas que podem ser analisadas em uma série econômica temporal, entretanto, as listadas acima são suficiente para gerar insights preciosos sobre a base de dados. Agora que entendemos o contexto e os pontos principais, vamos analisar duas séries econômicas reais: os dados do IPCA (medida oficial de inflação do Brasil) em 12 meses e mensal com o Python.
Exemplo real
Antes de tudo, é necessário ter em mãos a série, podemos realizar sua importação por meio do banco de dados do Banco Central utilizando a biblioteca python-bcb. Vamos portanto importar a biblioteca, bem como outras.
!pip install python-bcb
from bcb import sgs
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
plt.style.use('seaborn')
Existem diversos tipos de séries do IPCA e esse é um tópico mais especifico, mas para fins de relacionar com o histórico inflacionário do país, bem como comparar duas série apresentadas de formas distintas, vamos comparar o IPCA acumulado em 12 meses com a variação mensal do IPCA.
# Importa dados do IPCA acumulado em 12 meses (%)
ipca = sgs.get(('ipca', 13522), start = '1995-07-01')
# Importa dados do IPCA mensal (%)
ipca_month = sgs.get(('ipca', 433), start = '1995-07-01')
Agora que possuímos os dados, vamos utilizar principalmente o numpy, o pandas, o matplotlib, o seaborn e o statsmodels para criar as analises dos IPCAs.
Gráfico de Linha e Tendência
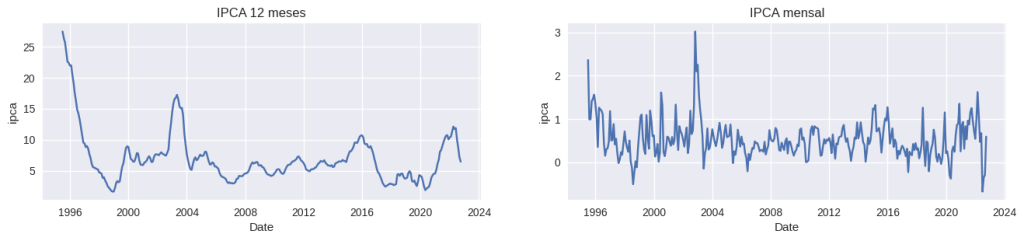
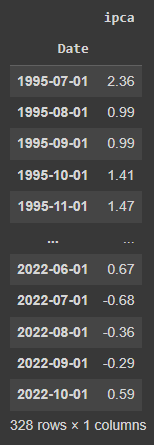
O primeiro passo será criar um gráfico de série temporal, isto é, um gráfico que representa uma linha contínua dos valores y do ipca, ao longo dos valores x da data da série.
fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100) # Configura dois plots no output
# Gráfico de linha do IPCA 12m
sns.lineplot(x = 'Date',
y = 'ipca',
data = ipca,
ax = axes[0]).set_title('IPCA 12 meses')
# Gráfico de linha do IPCA mensal
sns.lineplot(x = 'Date',
y = 'ipca',
data = ipca_month,
ax = axes[1]).set_title('IPCA mensal')
É visível a diferença dos valores entre as duas medidas, bem como o IPCA 12 meses possui pontos de tendência ao longo do tempo, enquanto o IPCA mensal mantem-se relativamente constante ao longo do tempo, apenas com alguns pontos extremos.
Estatística Descritiva
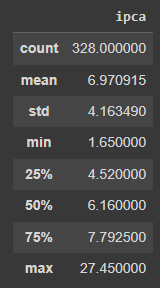
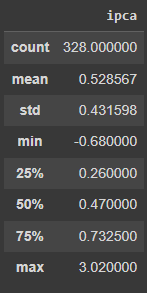
Outro ponto interessante é avaliar as principais estatísticas descritivas das séries a ponto de entender os valores de tendência central e de dispersão dos valores . É útil também avaliar por meio do método describe do pandas os percentis dos dados, permitindo avaliar a distribuição dos mesmo.
# Estatística Descritivas IPCA 12m ipca.describe()
# Estatística Descritivas IPCA mensal ipca_month.describe()
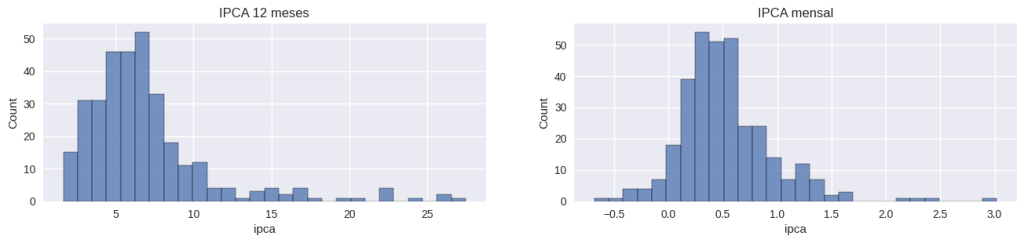
Histograma
O Histograma permite avaliar a frequência de valores do IPCA, isto é, permite entender quais os valores mais recorrentes da inflação no brasil nos últimos anos. Da mesma forma que os percentis, o histograma permite avaliar a distribuição dos valores das duas medidas.
fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100) # Configura dois plots no output
# Histograma IPCA 12m
sns.histplot(x = 'ipca',
data = ipca,
ax = axes[0]).set_title('IPCA 12 meses')
# Histograma IPCA mensal
sns.histplot(x = 'ipca',
data = ipca_month,
ax = axes[1]).set_title('IPCA mensal')
Sazonalidade
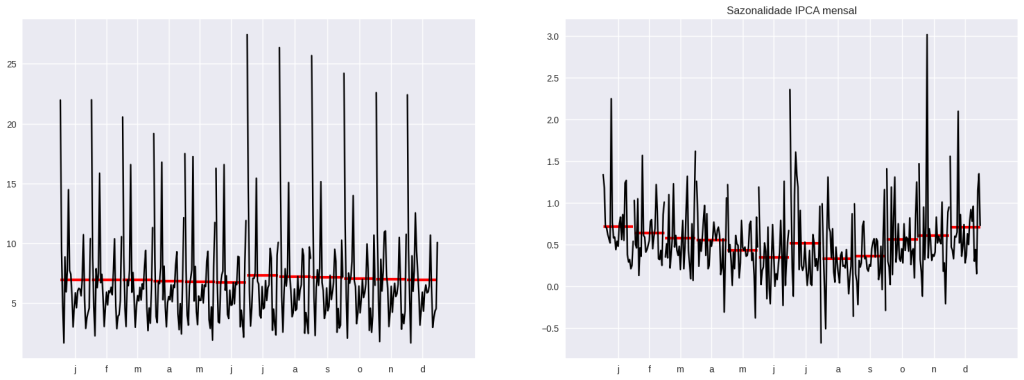
A Sazonalidade refere-se a períodos fixos em determinada frequência em que há um aumento ou decréscimo do valor da variável. É muito comum encontrar sazonalidade em séries econômicas e financeiras. Exemplo: aumento de vendas de sorvete no verão e queda no inverno.
No IPCA é possível verificar a sazonalidade de algumas formas, um meio é avaliando o gráfico de série temporal (em algumas séries é bem evidente o comportamento de sazonalidade no gráfico); outro pode ser pelo cálculo da média do mês de todos os anos e comparar com os demais, como no gráfico abaixo.
import statsmodels.api as sm
fig, axes = plt.subplots(1,2, figsize=(20,7), dpi= 100) # Configura dois plots no output
# Cria o gráfico da média e variações mensais IPCA 12m
ipca.index = pd.DatetimeIndex(ipca.index, freq='MS') # transforma a data em time index mensal
plt.title('Sazonalidade IPCA 12 meses')
sm.graphics.tsa.month_plot(ipca['ipca'], ax = axes[0]);
# Cria o gráfico da média e variações mensais IPCA mensal
ipca_month.index = pd.DatetimeIndex(ipca_month.index, freq='MS') # transforma a data em time index mensal
plt.title('Sazonalidade IPCA mensal')
sm.graphics.tsa.month_plot(ipca_month['ipca'], ax = axes[1]);
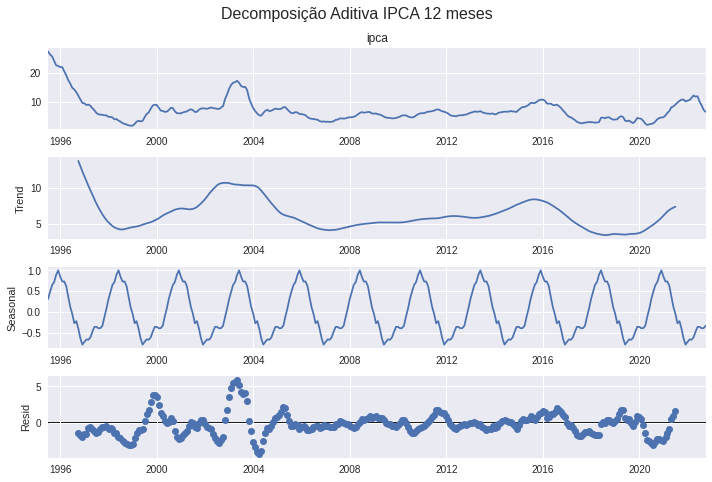
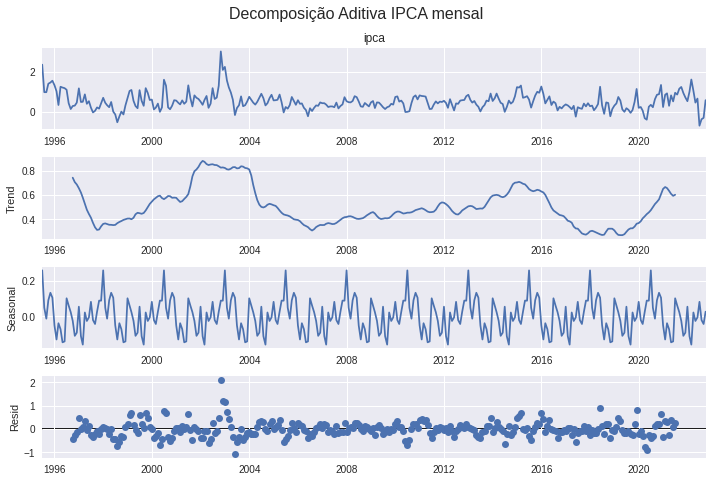
Decomposição
A decomposição de uma série temporal permite avaliar a tendencia, a sazonalidade e os valores restantes se retirado estes dois componentes.
from statsmodels.tsa.seasonal import seasonal_decompose
# Decomposição do IPCA 12 meses
plt.rcParams.update({'figure.figsize': (10,7)})
acum_decomposition = seasonal_decompose(ipca['ipca'], model='additive', period = 30)
acum_decomposition.plot().suptitle('Decomposição Aditiva IPCA 12 meses', fontsize=16);
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
# Decomposição do IPCA mensal
plt.rcParams.update({'figure.figsize': (10,7)})
month_dcomposition = seasonal_decompose(ipca_month['ipca'], model = 'additive', period = 30)
month_dcomposition.plot().suptitle('Decomposição Aditiva IPCA mensal', fontsize=16);
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
Autocorrelação
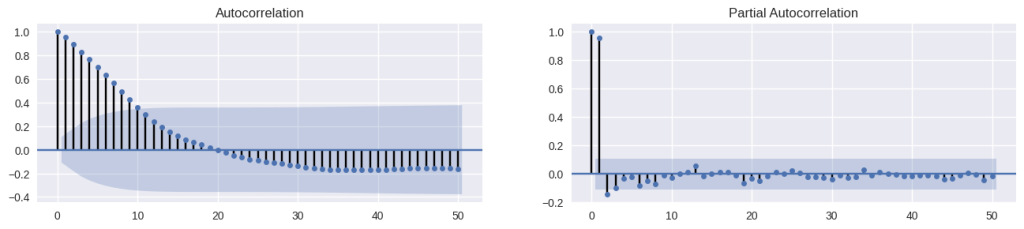
A autocorrelação é a identificação de possíveis correlações com os valores defasados (passados) da própria série. Quando ocorre de a série exibir forte tendência, há uma forte autocorrelação, principalmente as iniciais. Podemos averiguar a medida por meio de um gráfico de ACF e PACF.
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf # Autocorrelação IPCA 12 meses fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100) plot_acf(ipca['ipca'].tolist(), lags=50, ax=axes[0]); plot_pacf(ipca['ipca'].tolist(), lags=50, ax=axes[1]);
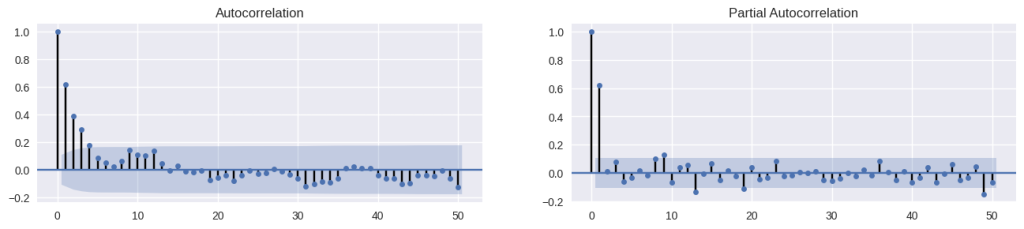
# Autocorrelação IPCA mensal fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100) plot_acf(ipca_month['ipca'].tolist(), lags=50, ax=axes[0]); plot_pacf(ipca_month['ipca'].tolist(), lags=50, ax=axes[1]);
Existem diversas outras ferramentas para explorar os dado de séries econômicas, entretanto, as averiguadas acima podem ser suficientes para o entendimento dos dados.
_____________________________________________
Quer saber mais?
Seja um especialista por meio da nossa trilha Ciência de dados para economia e finanças.