No Dicas de R dessa semana, iremos analisar alguns dados sobre espécies, utilizando a base de dados AnAge, disponibilizada no pacote (não disponível no CRAN) hagr. Para instalar ele, devemos rodar o código:
devtools::install_github("datawookie/hagr")
Após isso, basta carregar o pacote e teremos acesso aos dados.
library(hagr) library(tidyverse) library(ggplot2) library(wordcloud2) dados <- age levels(factor(dados$data_quality)) dados_limpos <- dados %>% filter((data_quality == "high" | data_quality == "acceptable") & kingdom == "Animalia" & (sample_size == "large" | sample_size == "medium"), phylum == "Chordata")
Devemos notar que o pessoal aqui da Análise Macro não é especializado em biologia, e as ferramentas utilizadas aqui no Dicas têm intuito de serem apresentadas apenas como modos de utilizar a programação em R, logo se houverem erros específicos ao tema, comentários são bem-vindos. Os dados contêm os nomes de cada espécie, e, como no post de semana passada, pode ser interessante verificar os animais com maior quantidade de espécies. Iremos fazer isso através de um wordcloud:
nomes <- dados_limpos %>% select(common_name) %>% mutate(principal = word(common_name, -1)) wordcloud2(table(unlist(nomes$principal)))
Como podemos ver, alguns dos animais com mais espécies são sapos, lagartos, morcegos e ratos. Outra relação que podemos verificar é entre a massa dos animais e sua taxa de metabolismo:
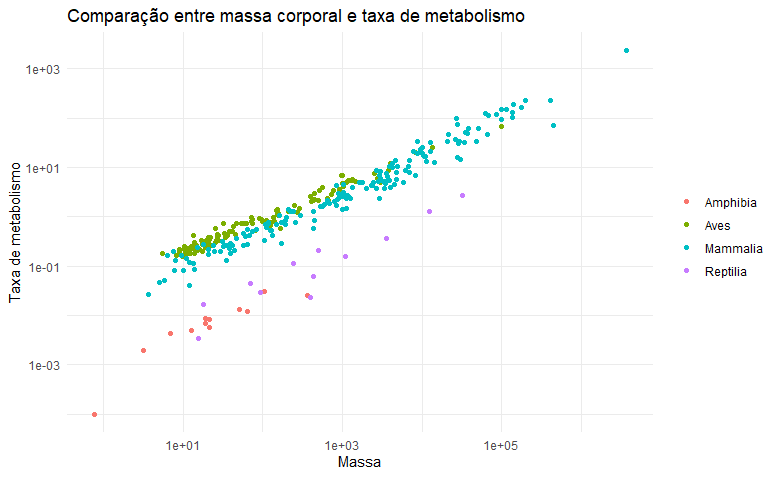
met <- dados_limpos %>% filter(metabolic_rate_watt>0) ggplot(data = met, aes(x=body_mass_g, y = metabolic_rate_watt, color = class)) + geom_point()+scale_x_continuous(trans = 'log10') + scale_y_continuous(trans = 'log10')+ labs(title = "Comparação entre massa corporal e taxa de metabolismo", x="Massa", y="Taxa de metabolismo")+ theme_minimal()+ theme(legend.title = element_blank())
Como podemos ver, a relação é crescente para todos os grupos que possuem dados. É interessante notar que animais de sangue quente, como mamíferos e aves, parecem ter - na média- taxas de metabolismo maiores do que animais de sangue frio, como répteis e anfíbios. Vamos então testar estatisticamente essa relação, analisando as populações de mamíferos e répteis - supomos aqui que espécies são amostras independentes, o que pode não ser verdade dependendo de quão próximos são os animais identificados, ferindo o TCL e inviabilizando o teste t de Student. Ademais, os dados para mamíferos não aparentam seguir distribuição normal, como podemos ver a seguir:
par(mfrow=c(1,2)) qqnorm(log10(filter(met, class=='Mammalia')$metabolic_rate_watt)); qqline(log10(filter(met, class=='Mammalia')$metabolic_rate_watt)) qqnorm(log10(filter(met, class=='Reptilia')$metabolic_rate_watt)); qqline(log10(filter(met, class=='Reptilia')$metabolic_rate_watt)) shapiro.test(log10(filter(met, class=='Mammalia')$metabolic_rate_watt)) shapiro.test(log10(filter(met, class=='Reptilia')$metabolic_rate_watt))
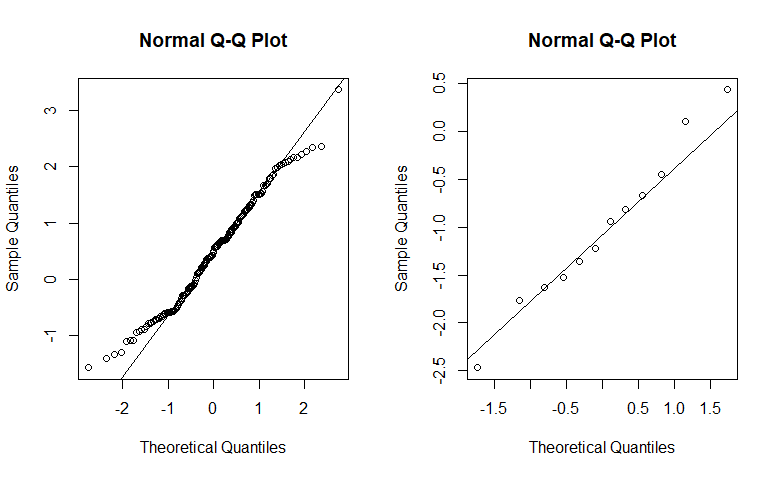
Além dos gráficos Q-Q, a estatística de Wilk-Shapiro para a amostra tem p-valor 0.04, indicando rejeição da hipótese nula de normalidade. Tanto o gráfico Q-Q como a estatística para répteis (p-valor de 0.99) indicam normalidade dessa amostra, logo o problema só ocorre com mamíferos. Com isso, como a amostra para mamíferos é grande (n=167), iremos aplicar o teste t, dado que a média das observações será razoavelmente normal. Ademais, para contornar a possibilidade do tamanho da amostra não ser grande o bastante - e também o problema de independência dentro de cada amostra já observado -, também iremos aplicar o teste de Wilcoxon-Mann-Whitney, que é não-paramétrico e não faz hipóteses sobre as distribuições das amostras. Os códigos para os testes são:
t.test(log10(filter(met, class=='Mammalia')$metabolic_rate_watt), log10(filter(met, class=='Reptilia')$metabolic_rate_watt), alternative = 'two.sided') wilcox.test(log10(filter(met, class=='Mammalia')$metabolic_rate_watt), log10(filter(met, class=='Reptilia')$metabolic_rate_watt))
O resultado dos testes é de p-valor menor que 0.01 para ambos, evidenciando assim que a média entre as duas populações é estatisticamente diferente.