No Dicas de R de hoje, vamos abordar o tema de redução de dimensionalidade. Esse tópico envolve extrair os principais dados de variáveis preditivas X quando temos um excesso delas em relação ao número de observações, de modo que a estimação por métodos usuais pode acabar falhando por ser impossível, ou por possuir variância muito grande quanto a seus parâmetros. Os dois métodos que serão apresentados hoje para resolver isso são a análise de componentes principais (PCA) e a regressão linear parcial (PLS).
A ideia por trás dessas ferramentas é transformar as variáveis originais em combinações que carregam a maior quantidade de informação possível. A partir de 
variáveis preditivas, teremos então 
variáveis do tipo
![\[Z_{m}=\sum_{j=1}^{p} \theta_{jm} X_{j}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-919fe1d65ed08543c54574a835df3102_l3.png "Rendered by QuickLaTeX.com")
Com isso, a regressão passa a ser:
![\[y_{i} = \beta_{0} + \sum_{m=1}^{M} \beta_{m}z_{im}+\epsilon_{i}, \;\;\;\;\;\; i = 1,\; ...,\; n\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-db1d372fbbde58871673fe828bbe821c_l3.png "Rendered by QuickLaTeX.com")
A regressão acima pode acabar enviesando a estimação, porém como trabalhamos com um número muito menor de restrições, a variância dos parâmetros é reduzida. Vamos falar agora sobre como selecionar as combinações lineares utilizadas.
Primeiramente, abordaremos o conceito de componentes principais. A ideia por trás desse método é capturar a direção de maior variação entre as variáveis preditivas, de modo a minimizar a soma das projeções dos pontos originais a essa reta. Com isso, as relações que ocorrem entre duas (ou mais) variáveis são "resumidas" em uma única variável sintética, que aproxima o valor onde estariam cada uma delas. Após isso, se quisermos capturar mais informações sobre a variação nos dados, podemos gerar um segundo componente principal, descorrelacionado com o primeiro, que absorve outras informações possíveis. Os dois componentes serão ortogonais, e podemos então gerar outros componentes ortogonais até termos número igual ao número de variáveis preditivas, extraindo todas as informações dos dados, porém isso seria equivalente a simplesmente regredirmos nos dados originais.
O ponto desse método é de que podemos capturar a maior parte das informações contidas em X através dos primeiros componentes principais, e então gerar uma regressão sobre eles, supondo que a direção de maior variação de X é a direção correlacionada com Y. É importante notar que a PCA não é capaz de escolher quais variáveis melhor explicam os dados: sua análise é feita sobre todo o X simultaneamente. Ademais, os dados trabalhados devem ser padronizados, pois, diferentemente da regressão linear usual, a regressão feita com PCA dará mais ênfase para variáveis de maior escala, pois sua variação é maior do que a das outras.
Para utilizar o método, iremos carregar o pacote pls. Faremos a análise dos dados do mtcars, buscando prever a variável mpg. Para compararmos o modelo com o PLS que iremos ver mais a frente, vamos utilizar 20 das 32 observações para treino, e deixaremos as últimas 12 como teste.
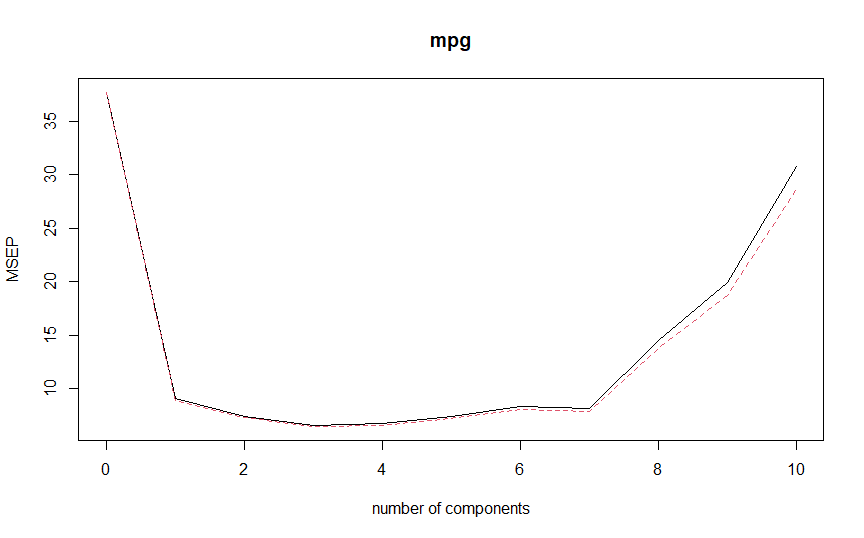
library(pls) train = sample(nrow(mtcars), 20) test = setdiff(1:nrow(mtcars), train) data_train = mtcars[train, ] data_test = mtcars[test, ] pcr.fit=pcr(mpg~., data=data_train, scale=TRUE, validation="CV") validationplot(pcr.fit, val.type="MSEP")
Acima, regredimos mpg contra todas as outras variáveis, fazendo a padronização (scale = TRUE) e utilizando validação cruzada para analisar o número ótimo de componentes. O resultado da validação cruzada é plotado no gráfico acima, indicando que o número de componentes principais que minimizou o erro quadrático médio de validação é 3. Ademais, com o summary() da função (não incluso aqui), podemos ver que os 3 componentes são capazes de explicar 90,2% da variação em X, e 85.8% da variação em mpg.
Vamos agora introduzir o método PLS. Diferentemente da PCA, que analisa as maiores variações dentro de X para utilizá-las como regressoras de Y, o PLS é um método supervisionado, de modo que ele identifica as combinações lineares que aproximam todas as variáveis. Para fazer isso, o primeiro componente 
da PLS é a combinação de todas as regressoras, utilizando como peso para cada uma o seu coeficiente na regressão simples de Y contra ela, que é proporcional à sua correlação com Y. Para encontrarmos o segundo componente, primeiramente fazemos a regressão de cada regressora X em , e extraímos o resíduo. O resíduo de todas as regressões é a variação das regressoras que não é contabilizada pelo primeiro componente, e o processo para gerarmos o próximo é o mesmo de antes, porém regredindo Y em cada um dos resíduos e tomando seu coeficiente.
Fazendo a regressão no R, usamos a função plsr():
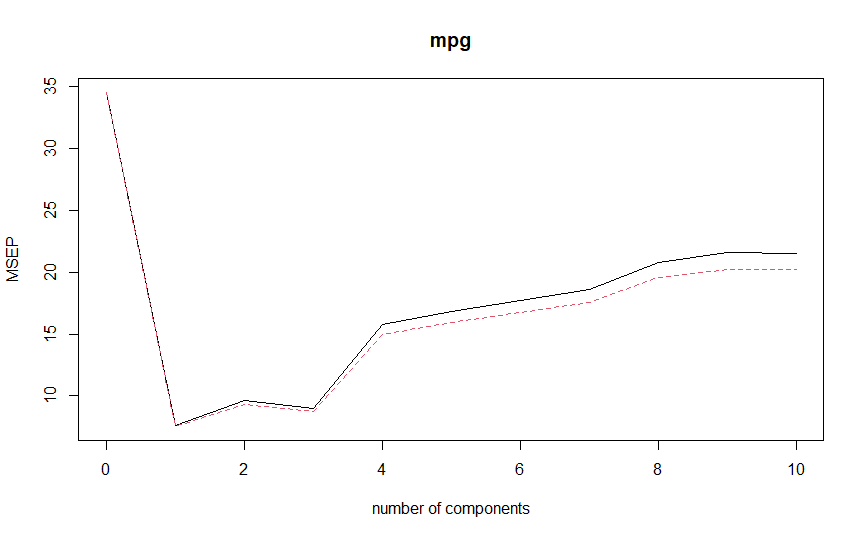
pls.fit = plsr(mpg~., data = data_train, scale = TRUE, validation = 'CV') validationplot(pls.fit, val.type="MSEP")
O resultado da validação cruzada indica que o erro quadrático médio é minimizado utilizando apenas 1 componente. Ele explica apenas 55,1% de X, porém explica 82,04% de mpg. Vamos então comparar os dois modelos escolhidos com os dados de teste separados previamente:
pcr.pred=predict(pcr.fit, data_test, ncomp=3) pls.pred=predict(pls.fit, data_test, ncomp=1) mean((pcr.pred-data_test[,'mpg'])^2) mean((pls.pred-data_test[,'mpg'])^2)
O resultado encontrado é 6.39 para o PCA e 6.59 para o PLS, indicando que o primeiro é ligeiramente melhor, porém ambos apresentam resultados interessantes.
Conteúdos como esse podem ser encontrados no nosso Curso de Machine Learning usando o R.
_____________________
