No Dicas de R de hoje, vamos apresentar métodos de árvore para a classificação e regressão de dados, e mostrar como utilizar random forests no R. Árvores nesse contexto são um conjunto de regras de decisão que se subdividem (como em galhos) para separar o espaço das variáveis regressoras em compartimentos que preveem um valor ou classe (as folhas). Nesse contexto, fica a dúvida: como podemos construir uma árvore de decisões?
Uma estratégia inicial pode ser iniciar em sua base (que, na notação utilizada, é o topo), onde temos basicamente a mesma previsão para todas as observações, e procurar qual regra para qualquer regressor leva à árvore que minimiza uma certa métrica, como o EQM. Dado esse passo, temos uma árvore com dois galhos, que divide o espaço em duas regiões. A partir daí, buscamos a próxima regra que minimiza a métrica (que pode gerar uma subdivisão em um dos galhos originais, ou gerar um terceiro galho a partir da base), e seguimos esse processo recursivamente. O método é simples, porém pode incorrer problemas de overfitting, e também apresentar grande variância na estimação.
Com isso, vamos verificar métodos de reduzir tal variância. A princípio, como só temos uma amostra, não podemos rodar várias vezes o modelo para combater a variância elevada, porém, podemos extrair subamostras aleatórias da amostra original e aplicar o modelo sob elas, método conhecido como bootstrapping. Para cada subamostra, podemos gerar uma árvore de decisão conforme descrito anteriormente, e então tomar a média das decisões para cada observação como decisão final.
O método acima é conhecido como bagging, e ele tem um problema: como sempre testa para todas as variáveis a regra de decisão que melhor diminui o erro, se uma variável possuir poder explanatório muito maior do que as outras, as árvores terão sempre galhos iniciais parecidos, logo a estimação é altamente correlacionada, diminuindo o poder do bootstrapping de reduzir a variância. Para resolver isso, introduzimos as random forests: além de tomar uma subamostra das observações originais, ao construir uma árvore de decisão, cada passo da árvore é feito utilizando apenas parte dos regressores como possíveis regra de decisão, escolhida aleatoriamente todas as vezes. Assim, em grande parte das árvores geradas, a variável de maior poder explanatório só será introduzida depois da primeira ramificação - em alguns casos, pode nunca aparecer -, fazendo com que as árvores sejam muito mais diversas sobre suas regras de decisão, tornando-as menos correlacionadas.
Vamos agora fazer um exemplo no R de random forests. Para isso, utilizaremos o dataset de preços medianos de casas Boston, do pacote MASS, e o pacote randomForest.
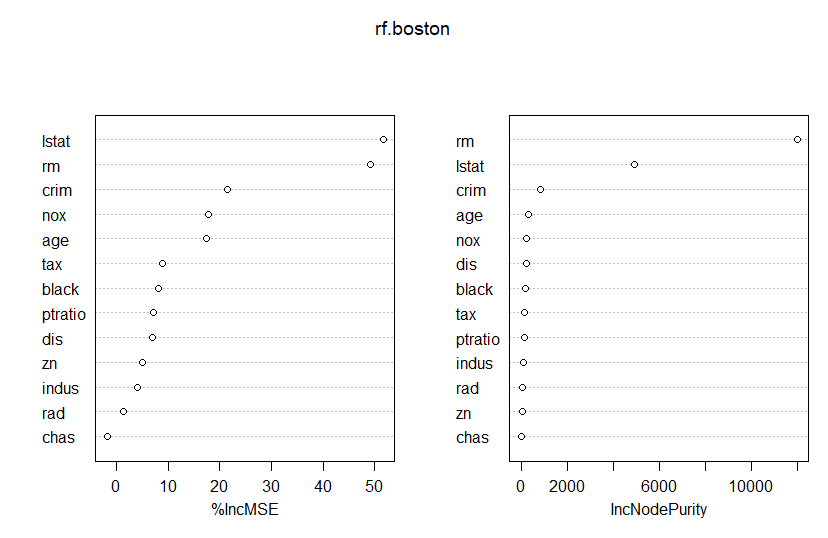
</pre> library(randomForest) library(MASS) set.seed(1) train = sample(1:nrow(Boston), nrow(Boston)/2) boston.test = Boston[-train, "medv"] rf.boston=randomForest(medv ~ . , data=Boston, subset=train, importance =TRUE) varImpPlot(rf.boston) <pre>
O resultado encontrado no plot acima é de que as variáveis que mais importam para a decisão são a riqueza da comunidade (lstat) e o tamanho das casas (rm).
Conteúdos como esse podem ser encontrados no nosso Curso de Machine Learning usando o R.
_____________________