No Hackeando o R de hoje, vamos apresentar métodos de análise de sobrevivência, e como podem ser estimados no R. Tais métodos buscam estimar o tempo esperado até que ocorra uma falha, como o tempo de vida de uma lâmpada, por exemplo. Um problema comum da literatura da área é o fato de que, dependendo do evento, estudos conduzidos podem acabar sem que alguns dos indivíduos tenham atingido tal falha, isso é, sabe-se apenas que a falha ocorre em um tempo maior do que o máximo do estudo. Desse modo, os dados são 'censurados à direita'.
Vamos iniciar a análise com o dataset lung, do pacote survival, que contém o tempo transcorrido até a morte de um paciente ou o final do estudo (o que ocorrer primeiro), a partir do momento do diagnóstico. Iremos visualizar esses dados com curvas de Kaplan-Meier, um estimador da função de sobrevivência da população, para tentar visualizar possíveis diferenças no tempo de vida de homens e mulheres.
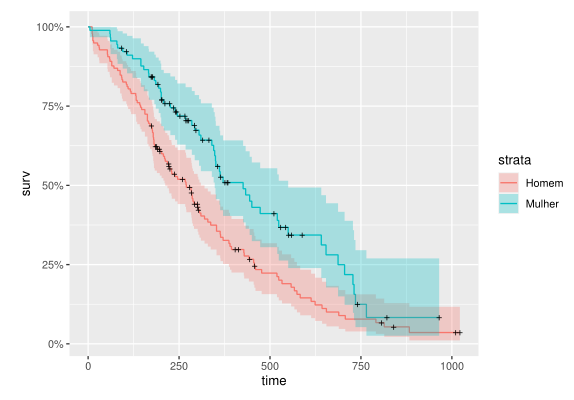
library(ggfortify) library(survival) library(tidyverse) dataset = lung %>% mutate(sex = ifelse(sex == 1, 'Homem', 'Mulher')) m = survfit(Surv(time, status) ~ sex, data = dataset) autoplot(m)
Como podemos ver, a estimação aparenta indicar para uma função de sobrevivência consistentemente menor para homens, de modo que seu tempo esperado de vida após o diagnóstico é, de modo geral, menor. Para não ficar apenas em palavras, vamos testar isso estatisticamente, usando o teste de Mantel-Cox:
survdiff(Surv(time, status) ~ sex, data = lung) survdiff(formula = Surv(time, status) ~ sex, data = lung) N Observed Expected (O-E)^2/E (O-E)^2/V sex=1 138 112 91.6 4.55 10.3 sex=2 90 53 73.4 5.68 10.3 Chisq= 10.3 on 1 degrees of freedom, p= 0.001
O p-valor do teste é quase 0, e, como a hipótese nula é de que as funções de risco são as mesmas, encontramos evidência em favor da conclusão do parágrafo anterior. Essa função de risco é a taxa de eventos em um tempo t, dado que o indivíduo sobreviveu até então. Podemos analisar como o tempo de sobrevivência é afetado por outros dados com o modelo de riscos proporcionais, estimado com a função coxph:
m2 <- coxph(Surv(time, status) ~ age + sex, data = lung) summary(m2) coxph(formula = Surv(time, status) ~ age + sex, data = lung) n= 228, number of events= 165 coef exp(coef) se(coef) z Pr(>|z|) age 0.017045 1.017191 0.009223 1.848 0.06459 . sex -0.513219 0.598566 0.167458 -3.065 0.00218 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 exp(coef) exp(-coef) lower .95 upper .95 age 1.0172 0.9831 0.9990 1.0357 sex 0.5986 1.6707 0.4311 0.8311 Concordance= 0.603 (se = 0.025 ) Likelihood ratio test= 14.12 on 2 df, p=9e-04 Wald test = 13.47 on 2 df, p=0.001 Score (logrank) test = 13.72 on 2 df, p=0.001
O valor exp(coef) indica como a razão de risco se altera com a mudança de uma variável, ceteris paribus. A cada ano adicional de vida, o risco se multiplica por 1.017, enquanto que, para uma mesma idade, mulheres apresentam apenas 60% do risco de homens, aproximadamente.
O modelo de riscos proporcionais pressupõe que o efeito das variáveis é o mesmo ao longo do tempo, o que muitas vezes pode não ser verdade. Uma outra opção é o modelo de aceleração do tempo de falha, onde as variáveis são responsáveis por mudar a velocidade do tempo de vida dos indivíduos. Para esse tipo de modelo, precisamos especificar uma distribuição a utilizar. No exemplo, utilizaremos a distribuição de Weibull, que é comum na literatura.
m_w <- survreg(Surv(time, status) ~ age + sex, data = lung, dist = "weibull") summary(m_w) survreg(formula = Surv(time, status) ~ age + sex, data = lung, dist = "weibull") Value Std. Error z p (Intercept) 6.27485 0.48137 13.04 < 2e-16 age -0.01226 0.00696 -1.76 0.0781 sex 0.38209 0.12748 3.00 0.0027 Log(scale) -0.28230 0.06188 -4.56 5.1e-06 Scale= 0.754 Weibull distribution Loglik(model)= -1147.1 Loglik(intercept only)= -1153.9 Chisq= 13.59 on 2 degrees of freedom, p= 0.0011 Number of Newton-Raphson Iterations: 5 n= 228 exp(coef(m_w)) (Intercept) age sex 531.0483429 0.9878178 1.4653368
Nesse caso, a interpretação de exp(coef) é mais simples, indicando a variação relativa do tempo esperado de vida. Como podemos ver, o modelo indica que mulheres têm um tempo de vida esperado 46% maior, ceteris paribus.
________________________
(*) Para entender mais sobre análises estatísticas, confira nosso Curso de Estatística usando R e Python.