No Hackeando o R de hoje, vamos concluir os posts dessa série de machine learning introduzindo métodos de clustering no R. Essas ferramentas são muito utilizadas para a análise de dados não-supervisionados, ou seja, dados que não possuem uma variável de resposta para servir como validação da previsão. Quando tratamos informações dessa natureza, o objetivo da modelagem estatística passa a ser então identificar subgrupos dentro das observações disponíveis, através da possível formação de agrupamentos (os chamados clusters) delas em regiões distintas no espaço dos seus possíveis valores. Com isso, vamos focar em dois métodos de agrupamento:o K-means clustering e o hierarchical clustering.
Para ilustrar, pense que você possui uma coleção de dados sobre clientes de sua loja, e quer identificar possíveis segmentos de mercado para especializar seus anúncios. Não há uma mensuração específica que indique que o indivíduo i faz parte do segmento y, porém, de posse dos dados de n indivíduos, podemos construir grupos de indivíduos que são estatisticamente parecidos.
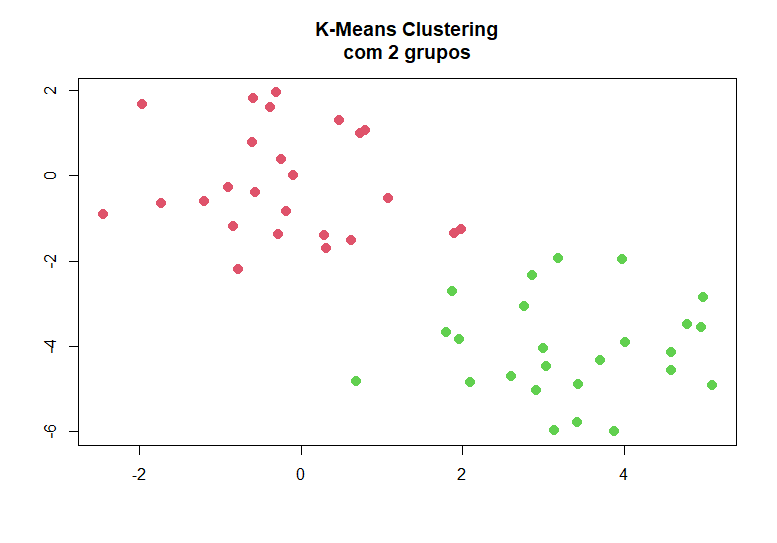
Nesse contexto, o método de K-means clustering busca gerar subgrupos que minimizam suas variâncias dentro de cada grupo. O ponto importante desse método é que ele exige que se escolha previamente o número de grupos que serão encontrados, e o algoritmo utilizado para gerar a divisão não necessariamente encontra o melhor resultado, então devemos rodá-lo múltiplas vezes. Abaixo, geramos dados que possuem dois grupos, e então testamos a função kmeans() do pacote base do R. Note que fornecemos ao R o número de grupos que queremos utilizar (k=2) e o número de vezes para rodar o modelo (nstart=20):
set.seed(2) x=matrix(rnorm(50*2), ncol=2) x[1:25, 1]=x[1:25, 1]+3 x[1:25, 2]=x[1:25, 2]-4 km.out=kmeans(x, 2, nstart=20) plot(x, col=(km.out$cluster+1), main= "K-Means Clustering com 2 grupos", xlab ="", ylab="", pch=20, cex=2)
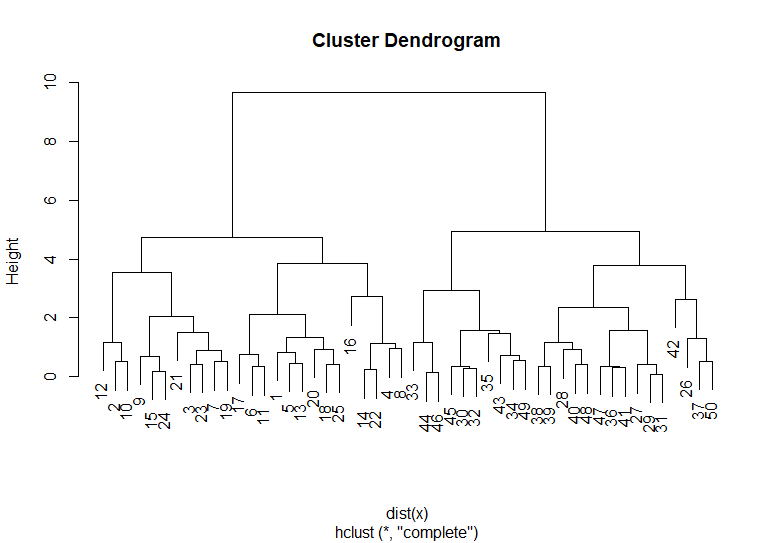
Já no caso do hierarchial clustering, não nos preocupamos tanto com a escolha de número de grupos, que é feita antes da análise e é relativamente arbitrária, e sim com o método de aproximação a ser feito. A análise hierárquica constroi uma árvore chamada dendrograma, cujas folhas são observações e os galhos são grupos de tamanho crescente conforme você se aproxima do tronco. Para gerarmos os grupos, primeiramente identificamos a distância entre cada uma das observações (considerando elas grupos de 1 indivíduo), e formamos o primeiro grupo com as duas mais próximas. Então, calculamos a distância entre todos os grupos (com alguma métrica pré-definida) e geramos o novo grupo com os dois mais próximos, e seguimos recursivamente até gerarmos a árvore final. Abaixo, geramos a árvore com nossos dados, considerando a distância entre os grupos como a maior distância entre um ponto de um grupo e um ponto de outro:
hc.complete=hclust(dist(x), method="complete") plot(hc.complete)
É importante notar que a distância horizontal entre as observações não reflete na sua distância real. No exemplo, a observação 42 parece mais próxima da 26 do que da 37 ou da 50, porém ela na verdade é próxima do cluster formado por essas 3. Com isso, o que importa para definirmos a proximidade é a distância vertical entre as observações no dendrograma. Com essa estrutura montada, podemos gerar os clusters escolhendo qual altura utilizar para seccionar a árvore. Abaixo, cortaremos a árvore em 2 clusters.
cutree(hc.complete, 2)
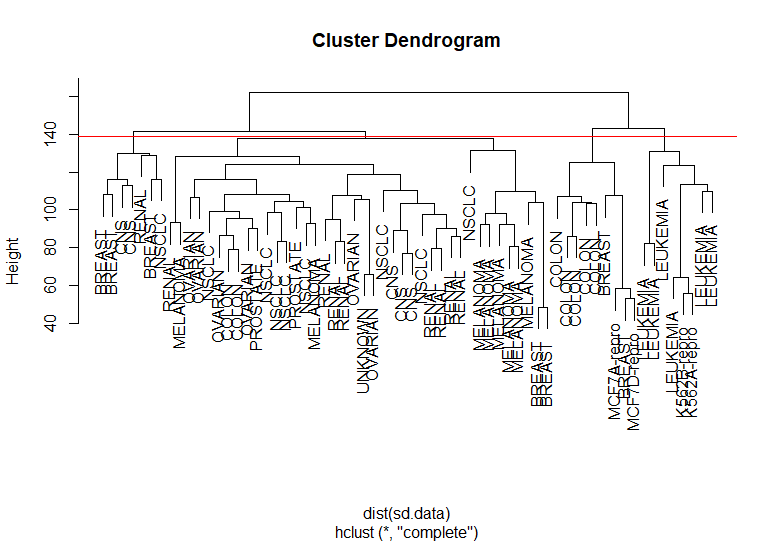
Como exemplo final, iremos aplicar os métodos sobre dados de células de câncer da base NCI60. Primeiramente, vamos padronizar os dados. Isso é importante pois variáveis de escala muito maior acabam dominando a variação de outras variáveis, tornando mais difícil encontrarmos relações entre elas.
library(ISLR) nci.labs=NCI60$labs nci.data=NCI60$data sd.data=scale(nci.data) data.dist=dist(sd.data)
Vamos agora cortar a árvore:
hc.out=hclust(dist(sd.data)) hc.clusters=cutree(hc.out, 4) plot(hc.out, labels=nci.labs) abline(h=139, col ="red")
Conteúdos como esse podem ser encontrados no nosso Curso de Machine Learning usando o R.
_____________________