No Hackeando o R de hoje, vamos apresentar métodos que são complementares ao post de semana passada. Enquanto a análise de sobrevivência era focada em observações que demoravam tempo demais para ocorrer (censuradas "à direita"), os métodos de hoje se interessam em lidar com o problema de dados que são censurados à esquerda. Isso pode ocorrer num contexto de testes de laboratório, como a mensuração da quantidade de certos elementos químicos na água, sendo que alguns dados podem não ser corretamente especificados por estarem em quantidade muito baixa, abaixo do limite de detecção das ferramentas do laboratório.
Os métodos apresentados no post sobre análise de sobrevivência conseguiriam (em tese) lidar com esse problema, porém na prática existem algumas diferenças que devem ser levadas em conta. Vamos começar nosso código carregando o pacote EnvStats, que contém funções construídas para lidar com dados não-detectados.
library(EnvStats)
Digamos que você possui observações de uma população que acredita que tem distribuição normal, porém os dados são censurados à esquerda. No código abaixo, geramos uma amostra nesse formato, criando 50 observações de uma normal com média 10 e desvio-padrão 3, e estabelecendo um valor mínimo de 8 para qualquer observação. Gravamos a média e desvio-padrão amostrais com e sem censura, para compararmos as estimativas posteriores.
# Normal(10, 3^2) x = rnorm(5000, 10, 3) mean_full = mean(x) sd_full = sd(x) # censura censored = 8 x[censored] = 8 mean_cens_naive = mean(x) sd_cens_naive = sd(x)
Para estimarmos a distribuição original, utilizaremos a função enormCensored, apropriada para a amostra dado que supomos que ela provém de uma dist. normal. Utilizaremos três métodos diferentes, cujos detalhes vão além do conteúdo desse post, e compararemos com o resultado de se estimar sem levar em conta a censura à esquerda. A função precisa apenas dos dados e de um vetor que indica quais observações foram censuradas.
estimates_mle = enormCensored(x, censored, method = "mle") estimates_bcmle = enormCensored(x, censored, method = "bcmle") estimates_ros = enormCensored(x, censored, method = "ROS") mean_full; sd_full [1] 9.951524 [1] 2.975333 mean_cens_naive; sd_cens_naive [1] 10.40674 [1] 2.337386 estimates_mle$parameters mean sd 9.970963 2.942115 estimates_bcmle$parameters mean sd 9.970817 2.942756 estimates_ros$parameters mean sd 9.951850 2.968289
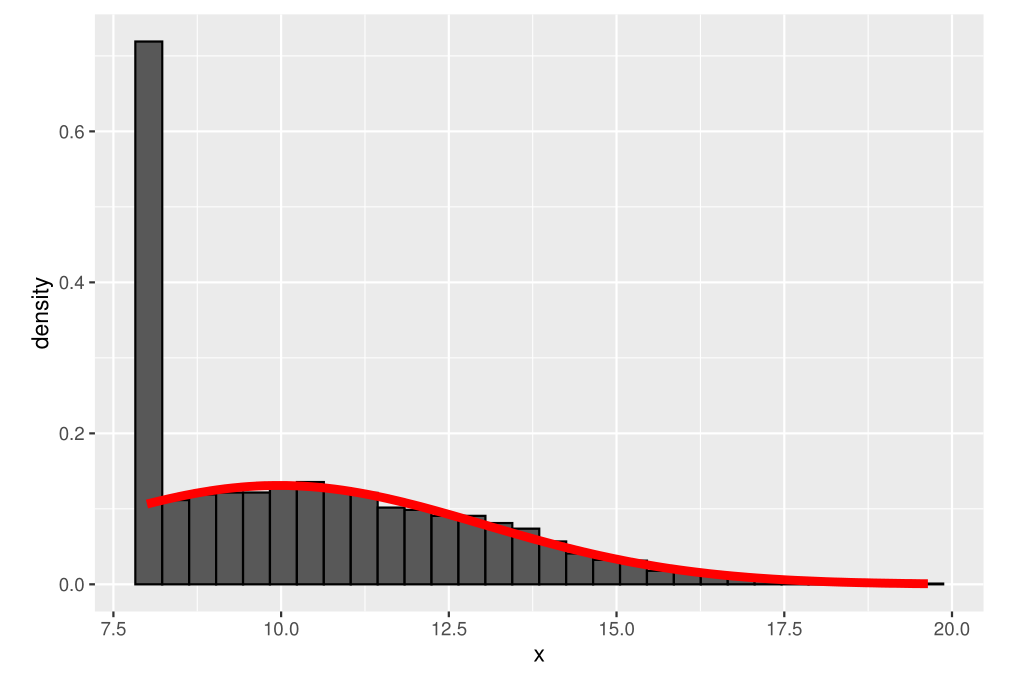
Como podemos ver, as estimativas de todos os modelos ficam muito melhores do que a estimativa 'ingênua'. Abaixo, visualizamos o histograma dos dados, em conjunto com a distribuição normal estimada pelo modelo.
library(ggplot2) ggplot(data.frame(x), aes(x)) + geom_histogram(colour = "black", aes(y = ..density..)) + geom_function(fun = dnorm, colour = "red", size = 2, args = list(mean = estimates_mle$parameters[1], sd = estimates_mle$parameters[2]))
Quanto ao caso de estarmos interessados em uma regressão com dados censurados, podemos utilizar o modelo Tobit, apropriado para isso. Vamos utilizar novamente o pacote survreg, para analisar o dataset EPA.92c.zinc.df do pacote EnvStats. O dataset contém mensurações de zinco em 5 poços, sendo composto de 8 observações para cada um, que foram feitas (por hipótese) em momentos diferentes.
library(survival) m = survreg(Surv(Zinc, !Censored, type = "left") ~ Sample + Well, data = EPA.92c.zinc.df, dist = "gaussian") summary(m) Call: survreg(formula = Surv(Zinc, !Censored, type = "left") ~ Sample + Well, data = EPA.92c.zinc.df, dist = "gaussian") Value Std. Error z p (Intercept) 2.435 3.422 0.71 0.477 Sample2 4.854 3.508 1.38 0.166 Sample3 4.012 3.554 1.13 0.259 Sample4 5.872 3.495 1.68 0.093 Sample5 3.036 3.571 0.85 0.395 Sample6 4.764 3.513 1.36 0.175 Sample7 5.655 3.501 1.62 0.106 Sample8 2.345 3.598 0.65 0.514 Well2 1.474 2.578 0.57 0.568 Well3 1.388 2.578 0.54 0.590 Well4 2.632 2.542 1.04 0.301 Well5 1.135 2.578 0.44 0.660 Log(scale) 1.497 0.181 8.29 <2e-16 Scale= 4.47 Gaussian distribution Loglik(model)= -72 Loglik(intercept only)= -74.7 Chisq= 5.58 on 11 degrees of freedom, p= 0.9 Number of Newton-Raphson Iterations: 3 n= 40
________________________
(*) Para entender mais sobre análises estatísticas, confira nosso Curso de Estatística usando R e Python.