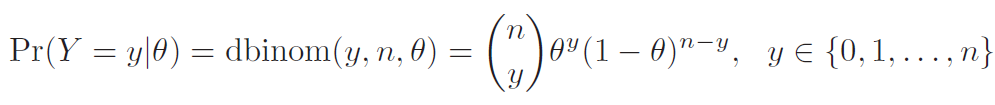No Hackeando o R de hoje, vamos fazer uma introdução à estatística bayesiana, passando pelos seus conceitos básicos e realizando um exemplo no R. Esse post será o primeiro de uma série sobre o tema, abordando temas mais avançados a cada semana.
A ideia por trás da estatística bayesiana é de que, a partir de uma crença prévia sobre os parâmetros que queremos estimar, é possível melhorar nosso conhecimento sobre seus valores verdadeiros através de uma amostra. Para realizar essa melhora, utilizamos o famoso Teorema de Bayes:
Pense no caso de uma variável com distribuição binomial, como uma amostra de pessoas que responderam a uma pergunta de 'sim' ou 'não'. Tal distribuição pode ser descrita como:
Note que a distribuição da amostra é dependente do parâmetro da binomial, que é o que queremos encontrar. Para resolvermos isso, basta traduzir nosso problema para o Teorema de Bayes: a probabilidade do parâmetro ser de certo valor, a partir dos dados, é igual à probabilidade dos dados serem gerados por esse valor, multiplicada pela probabilidade do parâmetro, dividia pela probabilidade total da amostra.
A probabilidade do parâmetro é escolhida previamente, pois é a nossa crença a priori quanto ao parâmetro verdadeiro, sobrando apenas a integral para calcularmos. De modo geral, a estimação dessa integral é o grande problema para a solução analítica de aplicações desse tipo, porém no caso que estamos utilizando de exemplo, essa questão se simplifica ao utilizarmos uma crença a priori uniforme entre 0 e 1. Considerando nosso exemplo de amostras de 'sim' ou 'não', e, dado que não temos nenhum estudo prévio sobre a proporção das respostas, tal crença parece válida, pois dá peso igual a todos os valores válidos para a proporção, que é o parâmetro de uma binomial.
Utilizando o Teorema de Bayes (e alguns resultados fora do escopo do nosso post), podemos chegar em uma fórmula fechada para a probabilidade a posteriori - isto é, a nossa nova crença, após olharmos os dados - do parâmetro estimado:
Com isso, a partir de uma amostra, podemos encontrar uma distribuição estimada para o valor verdadeiro da proporção. A distribuição uniforme para a crença a priori é um tipo particular da distribuição Beta, que é a posteriori acima. Quando as crenças são da mesma família, dizemos que elas são conjugadas.
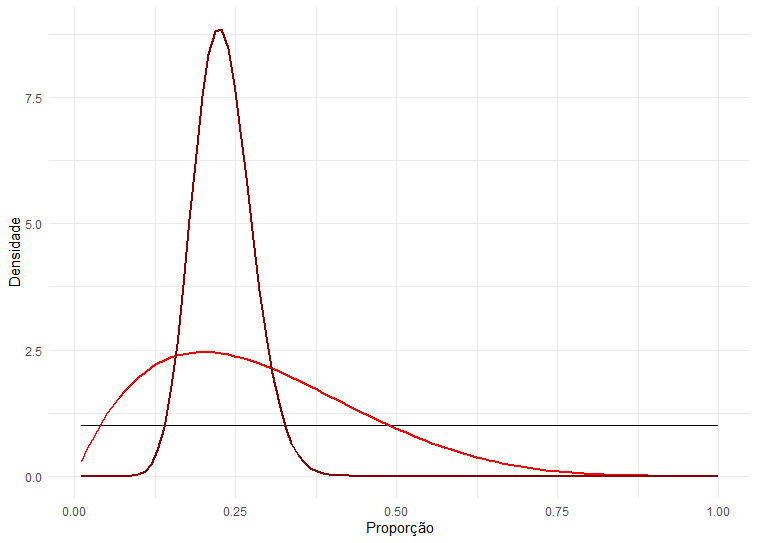
Digamos que possuímos duas amostras diferentes de tamanho 5 e 85, e ambas apresentam proporção de 'sim' de 20%. Utilizando a regra acima, podemos encontrar como fica a distribuição após computarmos a nova distribuição. Abaixo, temos um gráfico com a crença original (uniforme), e as outras duas. Como podemos ver, elas têm pico em torno da proporção da amostra, porém a distribuição com maior número de observações é muito mais estreita, indicando o maior nível de certeza que temos sobre o valor real do parâmetro.
library(ggplot2)
df = data.frame(x = seq(0.01, 1, by = 0.01), y = 1)
ggplot(df, aes(x=x, y = y)) + geom_line() +
stat_function(fun = function(x) dbeta(x, 2, 5), color = "red",
size = 1) +
stat_function(fun = function(x) dbeta(x, 20, 67), color = "darkred",
size = 1) +
xlab("Proporção") +
ylab('Densidade') +
theme_minimal(
)
________________________
(*) Para entender mais sobre análises estatísticas, confira nosso Curso de Estatística Bayesiana usando o R.