Regredir um variável ![]() contra uma variável
contra uma variável ![]() é um poderoso recurso estatístico. De modo a explicar o método, suponha que estamos interessados em estimar os parâmetros populacionais
é um poderoso recurso estatístico. De modo a explicar o método, suponha que estamos interessados em estimar os parâmetros populacionais ![]() e
e ![]() de um modelo de regressão simples
de um modelo de regressão simples
(1) ![]()
a partir de uma amostra aleatória de ![]() e
e ![]() . Os estimadores de Mínimos Quadrados Ordinários (MQO) serão
. Os estimadores de Mínimos Quadrados Ordinários (MQO) serão
(2) 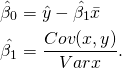
Baseado nos parâmetros estimados, a reta de regressão será
(3) ![]()
Para uma dada amostra, nós precisaremos calcular as quatro estatísticas ![]() ,
, ![]() ,
, ![]() e
e ![]() e colocá-las nessas equações. Para ilustrar, vamos considerar o exemplo 2.3 de Wooldridge (2013) sobre Salários de CEOs e Retornos sobre o patrimônio. Para isso, considere o seguinte modelo
e colocá-las nessas equações. Para ilustrar, vamos considerar o exemplo 2.3 de Wooldridge (2013) sobre Salários de CEOs e Retornos sobre o patrimônio. Para isso, considere o seguinte modelo
(4) ![]()
onde ![]() é o salário anual de CEO em milhares de dólares e
é o salário anual de CEO em milhares de dólares e ![]() é o retorno médio sobre o patrimônio em percentual. O parâmetro
é o retorno médio sobre o patrimônio em percentual. O parâmetro ![]() irá medir a variação no salário anual quando o retorno médio sobre o patrimônio aumentar em um ponto percentual. Para estimar esse modelo, podemos utilizar o conjunto de dados ceosal1. Podemos dar uma olhada nas variáveis do conjunto de dados cesal1 a partir do pacote wooldridge como abaixo.
irá medir a variação no salário anual quando o retorno médio sobre o patrimônio aumentar em um ponto percentual. Para estimar esse modelo, podemos utilizar o conjunto de dados ceosal1. Podemos dar uma olhada nas variáveis do conjunto de dados cesal1 a partir do pacote wooldridge como abaixo.
data(ceosal1, package='wooldridge') attach(ceosal1)
Uma vez que tenhamos carregado o conjunto de dados, podemos calcular manualmente os parâmetros ![]() e
e ![]() , como abaixo.
, como abaixo.
# Cálculo manual dos parâmetros b1hat = cov(roe,salary)/var(roe) b0hat = mean(salary) - b1hat*mean(roe)
Isto é, a reta de regressão será dada por
(5)
o que pode ser facilmente obtido com o código abaixo:
lm(salary ~ roe)
Implicando que para um , teremos um salário previsto de 963,19 ou US$ 963.191, que é o intercepto. Ademais, se
, então
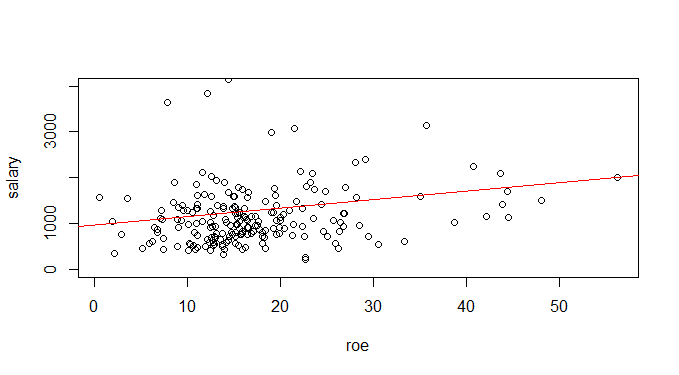
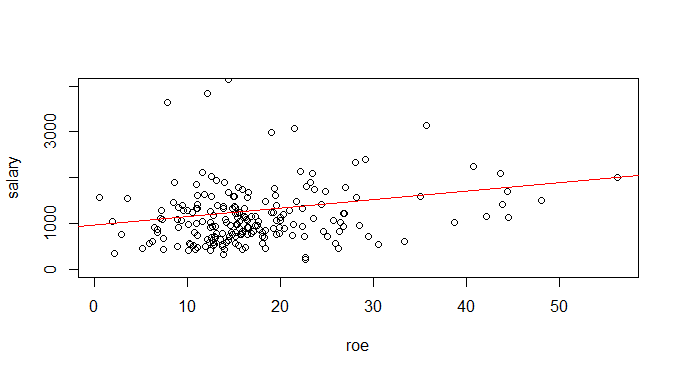
= 18,5 ou US$ 18.501. Podemos, por fim, desenhar a reta de regressão com o código abaixo.
CEOregress = lm(salary ~ roe) plot(roe, salary, ylim=c(0,4000)) abline(CEOregress, col='red')
Vamos continuar nossa revisão de modelos de regressão simples com o conjunto de dados wage1. Estamos interessados agora em estudar a relação entre educação e salários, de modo que o nosso modelo de regressão será
(6)
O que pode ser obtido com o código abaixo.
modelo = lm(wage ~ educ, data=wage1) modelo
Isto é, teremos a seguinte reta de regressão
(7)
de modo que um ano adicional de estudo implica em mais 54 centavos à hora de trabalho. O objeto obtido com a função lm contém todas as informações relevantes de uma regressão. Abaixo, acessamos os elementos do objeto CEOregress:
names(CEOregress) CEOregress$coefficients
Podemos obter os valores ajustados:
plot(CEOregress$fitted.values)
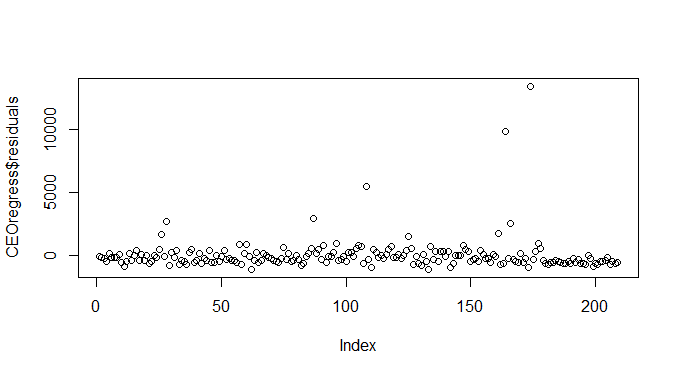
E os resíduos:
plot(CEOregress$residuals)
Por fim, podemos ainda obter um sumário de todas as estatísticas relevantes da regressão com a função abaixo.
summary(CEOregress)
O que podemos gerar como tabela com o pacote stargazer como abaixo.
| Dependent variable: | |
| salary | |
| roe | 18.501* |
| (11.123) | |
| Constant | 963.191*** |
| (213.240) | |
| Observations | 209 |
| R2 | 0.013 |
| Adjusted R2 | 0.008 |
| Residual Std. Error | 1,366.555 (df = 207) |
| F Statistic | 2.767* (df = 1; 207) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
Gostou? Isso e muito mais você aprende em nosso Curso de Introdução à Econometria usando o R.
__________________
(*) Wooldridge, J. M. Introductory Econometrics: A Modern Approach. Editora Cengage, 2013.