Introdução a modelos de Séries Temporais no R

Quais modelos podem ser utilizados para a previsão de séries temporais? No post, vemos a porta de entrada para compreender esse assunto, compreendendo a regressão linear de séries temporais e o alisamento exponencial.

Séries temporais são dados que são coletados ao longo do tempo, geralmente em intervalos regulares, e incluem informações sobre como esses dados mudam ao longo do tempo. Existem diversos tipos de modelos que tratam do uso desses tipos dados, veremos alguns deles a seguir.

Regressão Linear de Séries Temporais

A regressão linear de séries temporais é uma abordagem estatística que permite modelar a relação entre uma variável dependente e uma ou mais variáveis independentes, utilizando equações lineares. Essa técnica é particularmente útil quando se deseja prever valores futuros da série temporal com base em valores passados.

Regressão Linear Simples

No caso mais simples, o modelo de regressão permite uma relação linear entre a variável de previsão y e uma única variável preditora x.

$y_t = \beta_0 + \beta_1 x_t + \varepsilon_t.$

Os coeficientes $\beta_0$ e $\beta_1$ denotam a interceptação e a inclinação da linha, respectivamente. A interceptação $\beta_0$ representa o valor previsto de y quando x = 0. A inclinação $\beta_1$ representa a mudança média prevista em y resultado de um aumento de uma unidade em x.

Podemos pensar que cada observação de $y_t$ consiste na parte sistemática ou explicada pelo modelo $\beta_0 + \beta_1 x_t$ e um termo de erro $\varepsilon_t$ . O termo de erro não implica uma falha, mas um desvio em relação a reta estimada do modelo. Portanto, captura tudo que pode afetar $y_t$ além de $x_t$ .

Para obter o código de importação do dataset, da construção do modelo e também dos códigos subsequentes, faça parte do Clube AM, o repositório especial da Análise Macro.

Exemplo no R

Vejamos um exemplo no R. Usando o pacote {fpp3}, podemos encontrar diversas séries. No caso abaixo, usamos o dataset us_change que contém as séries de variações trimestrais de variáveis econômicas do EUA.

Podemos realizar um relacionamento entre o Consumo e Renda, plotando o gráfico de linha abaixo.

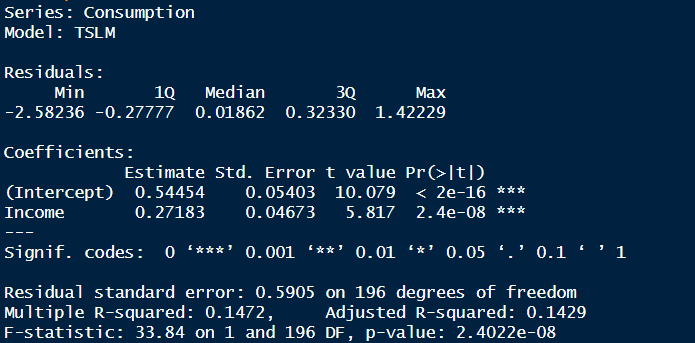
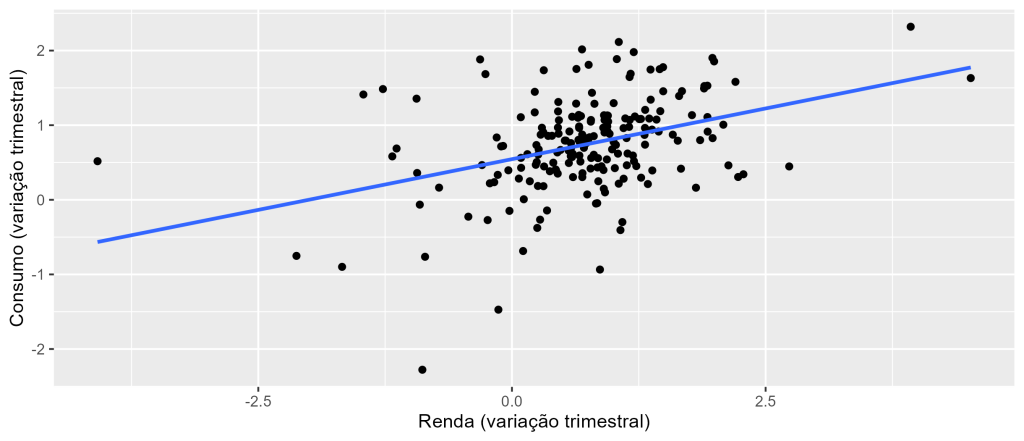
É possível perceber o relacionamento entre ambas as variáveis. Vamos confirmar usando um modelo de Regressão Linear e criando um gráfico de dispersão com a reta de regressão para compreender o relacionamento.

As estatísticas e o gráfico sugerem que há um forte relacionamento entre as variáveis no tempo.

Regressão Linear Múltipla

Quando há duas ou mais variáveis preditoras, o modelo é chamado de modelo de regressão múltipla. A forma geral de um modelo de regressão múltipla é

(1) $\begin{equation*} y_t = \beta_{0} + \beta_{1} x_{1,t} + \beta_{2} x_{2,t} + \cdots + \beta_{k} x_{k,t} + \varepsilon_t, \end{equation*}$

Onde $y_t$ é a variável a ser prevista e $x_1, \cdots x_k são as k variáveis preditoras$ . Cada variável necessita ser numérica. Os coeficientes $\beta_{k}$ mensuram o efeito de cada preditor.

Exemplo no R

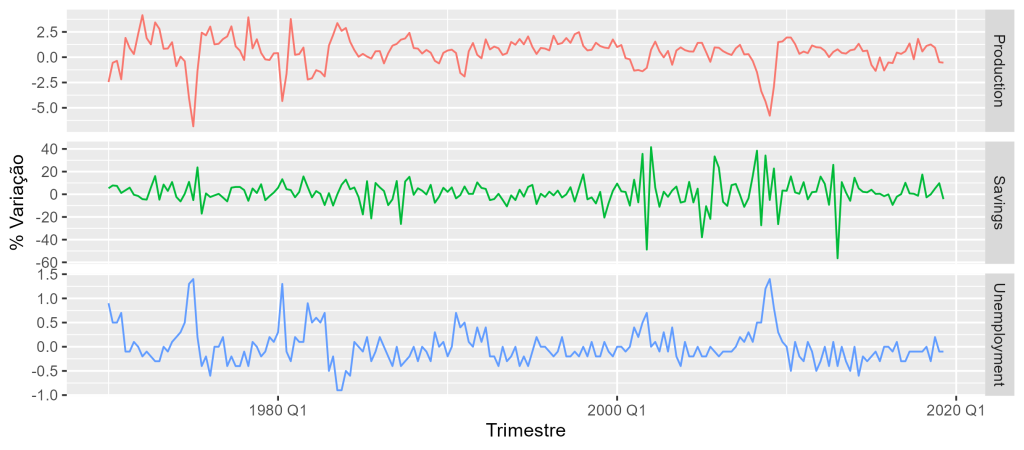
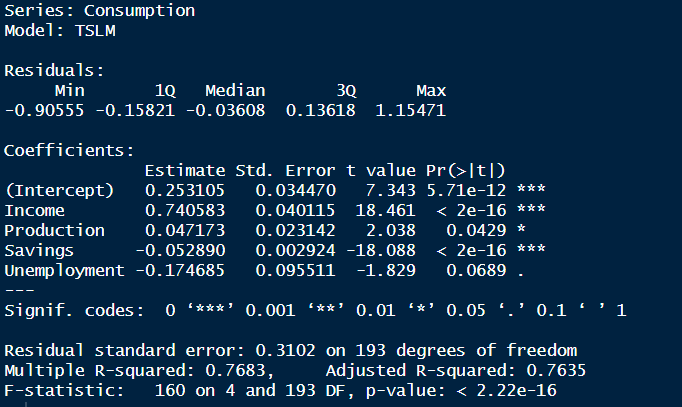
Continuando com o exemplo do pacote {fpp3}, us_changes, podemos averiguar não somente o relacionamento entre duas variáveis, mas também de diversas outras. Adicionamos no modelo de regressão as variáveis de Produção, Poupança e Desemprego para compreender os seus efeitos sobre o consumo.

Pelo gráfico e resultado do modelo, compreendemos que há de fato um relacionamento entre as variáveis ao longo dos trimestres.

Exponential Smoothing (Alisamento exponencial)

O alisamento exponencial é uma técnica estatística utilizada para prever valores futuros de uma série temporal, com base em seus valores passados. Essa técnica é especialmente útil quando se deseja prever valores em um horizonte de tempo curto, em que a influência dos valores mais recentes é mais significativa.

O alisamento exponencial funciona aplicando um peso exponencial decrescente aos valores da série temporal. Isso significa que os valores mais recentes têm um peso maior do que os valores mais antigos. O alisamento exponencial também leva em consideração a tendência geral da série temporal e, em alguns casos, a presença de sazonalidades.

Existem diferentes tipos de alisamento exponencial, incluindo o simples, o duplo e o triplo, que variam na quantidade de fatores de ponderação considerados. Cada tipo de alisamento exponencial é adequado para diferentes tipos de séries temporais e objetivos de previsão.

A previsão no tempo t + 1 é igual a média ponderada entre a observação mais recente y_t e a previsão anterior \hat{y_t+1|t}:

$\hat{y}_{t+1|t} = \alpha y_t + (1-\alpha) \hat{y}_{t|t-1}$

onde $0 \le \alpha \le 1$ é o parâmetro de alisamento para $t=1,\dots,T$

Exemplo no R

Podemos construir no R os valores estimados de y do modelo de Alisamento Exponencial utilizando como exemplo as Exportação da a em % do PIB anual. Além de construir os valores ajustados, realizamos a previsão dos valores em 5 anos a frente.

Referências

Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-01-18.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Como coletar dados do Eurostat usando a API com o Python?

Estimando a volatilidade da taxa de câmbio

Como analisar o Núcleo de Inflação no Brasil usando Python?

Propensity Score com Múltiplas Variáveis no R

Análise regional da inflação com dados do IBGE usando Python

Como coletar dados do Banco Central do Chile usando a API com o Python?

Outros artigos relacionados

Como coletar dados do Eurostat usando a API com o Python?

Neste artigo mostramos como pesquisar e como coletar os dados do portal Eurostat através do sistema de API usando a linguagem Python. Este processo permite automatizar rotinas de extração de dados, eliminando trabalho manual e repetitivo de atualização de bases de dados econômicos.

Estimando a volatilidade da taxa de câmbio

O que é Volatilidade? Como podemos calcular essa métrica? Este artigo apresenta uma breve introdução à volatilidade, descreve como podemos calcular a volatilidade utilizando Modelos de Volatilidade Condicional e demonstra a aplicação prática dessa abordagem para estimar a volatilidade da taxa de câmbio BRL/USD por meio da linguagem de programação Python.

Como analisar o Núcleo de Inflação no Brasil usando Python?

O Python se destaca como uma ferramenta robusta para análise de dados, permitindo a aplicação de uma ampla gama de técnicas em dados econômico-financeiros. Neste exercício, destacamos como a linguagem oferece uma facilidade muito grande na coleta de dados dos núcleos do IPCA diretamente do site do Banco Central, na manipulação eficiente desses dados e na construção de gráficos que facilitam a compreensão dos indicadores.