Introdução à Séries Temporais

Uma série temporal é, basicamente, uma sequência de observações tomada ao longo de um período de tempo. Em termos um pouco mais formais, como posto em Bueno (2011), dizemos que uma série temporal é uma possível realização de um processo estocástico, sendo este uma sequência de variáveis aleatórias. Diversos conjuntos de dados se apresentam como uma série temporal, como a taxa de desemprego, os juros básicos de uma economia, o PIB, a taxa de inflação, etc, o que torna esse campo da econometria extremamente importante. Para além da economia, há também aplicações do que chamamos de econometria de séries temporais na engenharia, nos negócios, nas ciências naturais, nas ciências sociais, etc.

Como posto em Enders (2009), "(...) the task facing the modern time-series econometrician is to develop reasonably simple models capable of forecasting, interpreting and testing hypotheses concerning economic data".

A econometria de séries temporais estará, nesse contexto, preocupada em explicar o passado de uma determinada variável, construir relações entre variáveis distintas e gerar previsões para alguns períodos à frente. Para isso, devemos construir modelos, simplificações da realidade que buscam ressaltar algumas características importantes das séries em que estamos interessados.

# Séries Temporais e Processos Estocásticos

Sendo um pouco mais formal, podemos verificar como os conceitos de série temporal e processo estocástico se relacionam. Usando Pfaff (2008),

Um processo estocástico é uma sequência ordenada de variáveis aleatórias, podendo ser definido formalmente como

(1)  

onde, para cada é uma variável aleatória no espaço amostral , e a realização desse processo estocástico é dada por para cada com respeito a um ponto no tempo . Consequentemente, \textbf{a série temporal que observamos é uma realização particular de um processo estocástico desconhecido}. Ela pode ser representada como segue

(2)  

Nesses termos, esse processo estocástico desconhecido é o que chamamos de processo gerador dos dados que formam uma série temporal. Cada em é, desse modo, apenas um valor possível de uma variável aleatória. Uma variável aleatória, por seu turno, é aquela que assume valores numéricos e tem um resultado que é determinado por um experimento. Para maiores detalhes sobre fundamentos estatísticos, ver, por exemplo, os apêndices de Wooldridge (2013). O desafio do econometrista será, portanto, tendo acesso apenas à série temporal, buscar compreender esse processo estocástico desconhecido. Quanto melhor for essa compreensão, melhor será a modelagem e, com efeito, a previsão de observações futuras.

# Decomposição de uma série temporal

De modo a compreender o processo gerador de dados de uma determinada série temporal, pode ser interessante decompô-la em alguns componentes. Como em Cowpertwait et al. (2009)

(3)  

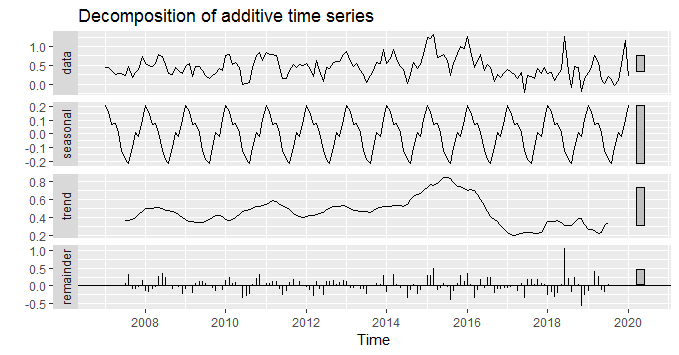
Onde, no tempo , é uma série temporal, é uma tendência, é um efeito sazonal e é um termo de erro. No , podemos fazer essa decomposição com a função decompose, como abaixo.

### Importar e decompor dados da Inflação
inflacao = Quandl('BCB/433', order='asc', type='ts',
start_date='2007-01-01')
inflacao %>%
decompose %>%
autoplot

Escolhemos acima a série de inflação medida pelo Índice de Preços ao Consumidor Amplo (IPCA). Observe o leitor que é possível verificar os dados observados, um componente de tendência, a parte sazonal e um termo de erro. Como veremos ao longo do nosso curso de Séries Temporais usando o R, identificar corretamente esses componentes é um passo importante para compreender o processo gerador de dados de uma série.

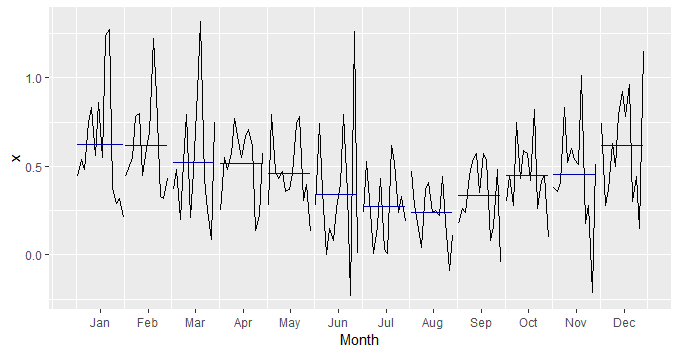
# Sazonalidade

Como vimos acima, a inflação apresenta um componente sazonal bastante nítido.

ggmonthplot(inflacao)

Isto é, em um ano calendário, uma série pode apresentar um comportamento que se repete.

# Estacionariedade

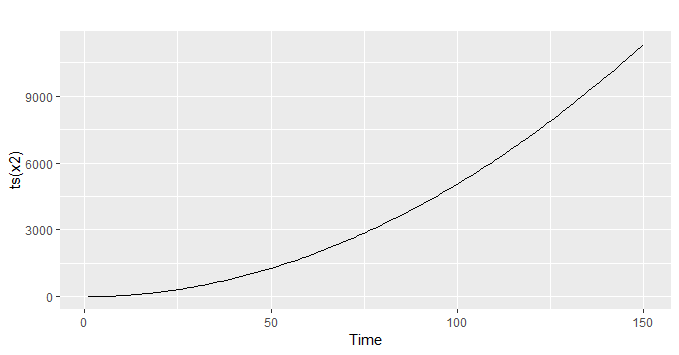
Uma característica extremamente importante de uma série temporal, que percorrerá praticamente todo o nosso curso de Séries Temporais usando o R, é o de estacionariedade. Como vimos acima, uma série temporal nada mais é do que a realização particular de um processo estocástico. Essa realização, contudo, pode ser estacionária ou não. Observe, por exemplo, a série abaixo.

n <- 150
eps <- rnorm(n)
trend <- seq_len(n)
x2 <- rep(0, n)
for (i in seq.int(2, n)){
x2[i] <- trend[i] + x2[i-1] + eps[i]
}

autoplot(ts(x2))

Ao olhar a série acima, chama atenção a tendência da mesma. Significa dizer que se estivéssemos interessados em modelar a série, teríamos de levar essa tendência crescente em consideração. Isso é, de fato, um problema. Para entendermos melhor essa questão, vamos definir o que seja uma série estacionária.

Com base em Enders (2009), podemos assumir que um processo estocástico, tendo uma média e variância finitas, será covariância estacionário se para todos e ,

(4)  

onde , e são todas constantes. Em termos simples, desse modo, uma série temporal é convariância estacionária se sua média e todas as autocovariâncias não são afetadas por mudanças na origem do tempo. Em outras palavras, como explica Wooldridge (2013), 'a estacionariedade da covariância enfatiza somente os primeiros dois momentos de um processo estocástico: a média e a variância do processo são constantes no decorrer do tempo e a covariância entre e depende somente da distância entre os dois termos, h, e não da localização do período de tempo inicial, t.'

A estacionariedade é extremamente importante para a modelagem de uma série temporal. Isso porque, suponha que estejamos regredindo contra . Se estivermos lidando com séries não estacionárias, isso implica que os coeficientes que encontrarmos não serão representativos da relação entre elas. Estaremos, assim, encontrando uma relação espúria. Logo, antes de construir um modelo econométrico, precisaremos nos certificar se as séries em questão são, de fato, estacionárias ou, claro, lidar com esse fato através de algum outro procedimento, como veremos mais à frente nesse curso.

# Tipos de modelos de séries temporais

Há, basicamente, duas formas de se entender uma série temporal, do ponto de vista econométrico. Modelos de série temporal podem ser:

Modelos Univariados - as características da série de interesse são explicadas exclusivamente a partir do comportamento da própria série;

Modelos Multivariados - as características da série de interesse são explicadas não apenas em função da própria série, mas também por outras séries. Os modelos multivariados podem ser escalares, quando há apenas uma única equação, ou vetoriais, quando há múltiplas equações.

Quando se utilizará uma ou outra forma de modelagem vai depender muito das características da nossa série de interesse, como veremos ao longo do nosso curso.

___________________

(*) Isso e muito mais você aprende em nosso curso de Séries Temporais usando o R