Teste A/B é uma técnica criada com o intuito de comparar e testar a efetividade e benefícios de diferentes versões de programas ou mudanças em estratégias de negócios antes de tomar uma decisão final. O teste é uma forma bastante interessante de testar novas ideias, e portanto, pode ser muito útil para a avaliação de qualquer programa de uma empresa. No post de hoje, mostraremos como utilizar o Teste A/B em um exemplo prático com o R.
Imagine o seguinte: você e seus gestores querem saber se uma mudança no visual da página do site de compra de um curso pode levar a um aumento da compra pelos clientes. Seria difícil imaginar qual seria o impacto sem antes tentar a mudança. Para tanto, o Teste A/B permite criar experimentos, separando os sites em dois formatos, e avaliar estatisticamente as diferenças de compras entre ambos.
Em suma, é possível estabelecer as seguintes regras: seria A melhor do que B? Uma layout A atrairia mais clientes do que o B? A cor A é mais lucrativa que a B?
As duas versões daquilo que você deseja testar são chamadas de controle (a versão atual) e a de tratamento (modificada). As amostras desses dois grupos devem possuir tamanhos similares, bem como sua amostragem deve ser feita com os devidos cuidados (dados não viesados, períodos não tão curtos e nem tão longos para a coleta e a escolha correta do período a ser analisado e comparado, evitando sazonalidades e tendencias).
Variáveis
Ao criar um Teste A/B, é necessário cumprir os seguintes passos:
- Pergunta: A alteração em um programa vai resultar em qual efeito?
- Hipótese: Usar A ao invés de B resultará em mais benefícios para a empresa?
- Variável dependente: A variável A
- Variável Independente: A variável B.
Exemplo
Como exemplo, vamos utilizar o dataset WA_Marketing-Campaign, enviado por Anastasiia Chebotina na plataforma Kaggle.
" Uma rede de fast-food planeja adicionar um novo item ao seu cardápio. No entanto, ainda estão indecisos entre três possíveis campanhas de marketing para promover o novo produto. Para determinar qual promoção tem o maior efeito nas vendas, o novo item é introduzido em locais em vários mercados selecionados aleatoriamente. Uma promoção diferente é usada em cada local e as vendas semanais do novo item são registradas nas primeiras quatro semanas."
Objetivo: Avaliar os resultados do Teste A/B e decidir qual campanha de marketing melhor funciona.
Colunas:
- MarketID: identificação do mercado
- MarketSize: tamanho do mercado por vendas
- LocationID: identificação do local da loja
- AgeOfStore: idade da loja em anos
- Promotion: identificação das três promoções de marketing que devem ser testadas
- week: identificação das quatro semanas que as promoções foram ativadas
- SalesInThousands: volume de vendas para um local especifico com base no LocationID, Promotion, e week
Vamos construir os passos:
- Pergunta: Qual das promoções de marketing resultará em mais vendas para as lojas?
- Hipótese: Há uma diferença de valores por vendas entre as 3 promoções?
- Variável dependente: variável SalesInThousands;
- Variável Independente: variável Promotions.
Para começar, iremos realizar uma breve análise exploratória de dados para conhecer o dataset.
Primeiro, devemos importar os dados e checar sua estrutura. Há um problema logo de inicio. Os identificadores, que deveriam ser categorias, são expressos em números, o que leva o R a ler como tipo numérico. Realizamos a alteração das colunas para o tipo factor.
Com a mudança, podemos analisar as estatísticas descritivas do conjunto de dados com o pacote {skimr}. O interessante é perceber o número de contagem de cada categoria das variáveis. Em MarketSize, percebemos que há maior quantidade de mercados médios, com 320, em seguida grandes, com 168, e por fim pequenos com 60.
Em relação ao número de observações por promoções, é importante notar que entre as 3, há um número bem próximo com 188 da promoção 2, 188 da promoção 3 e 172 da promoção 1.
Já as variáveis numéricas, como a Idade da loja, vemos que é bem amplo a idade, com lojas de 1 ano de funcionamento até 28 anos.
Por fim, as vendas também apresentam valores bem amplos, de 17.3 até 99.6. Importante notar o desvio padrão de 16.8%.
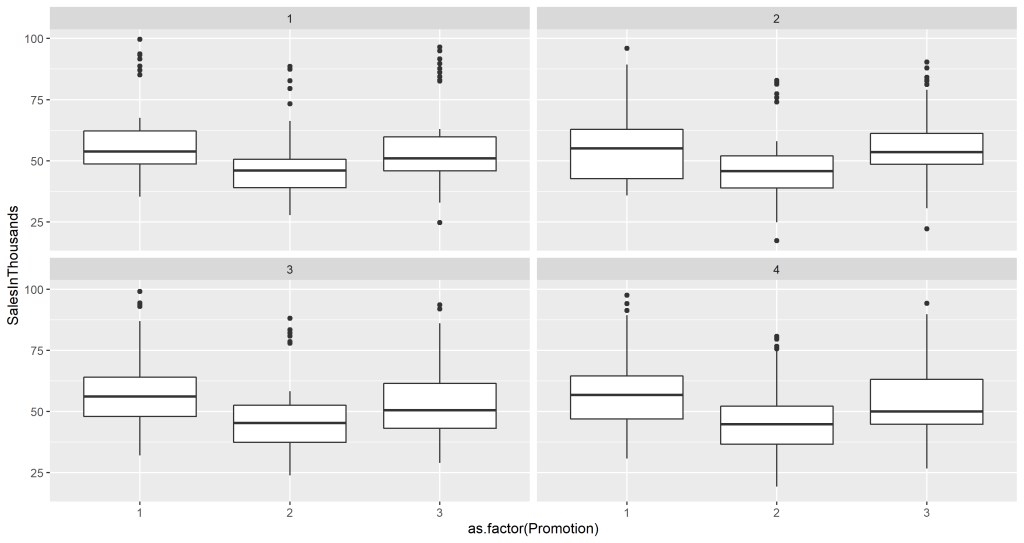
Como queremos saber qual promoção resultará em maiores vendas, é necessário investigar a variável promoção e vendas. Como vimos anteriormente, as vendas possuem valores discrepantes, portanto, iremos analisar em conjunto com a semana, de forma a entender se o efeito da diferença de tempo resultou nesse efeito.
Como houve pouca mudança nos gráficos ao longo das semanas, podemos entender que o tempo não teve efeito significativo. Entretanto, podemos já entender que há alguma diferença no número de vendas em relação a cada promoção de marketing.
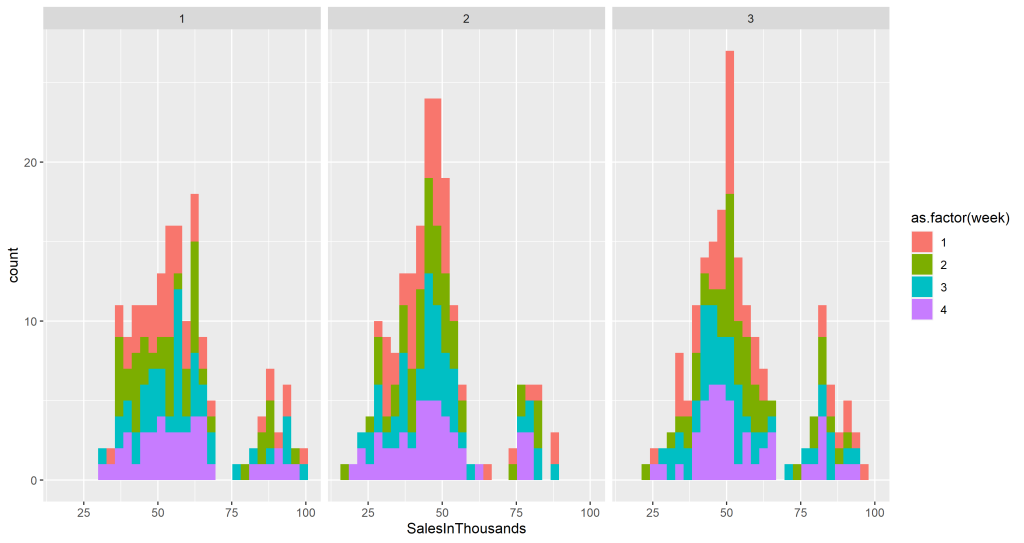
Antes de prosseguir com o teste da hipótese criada (Há uma diferença de valores por vendas entre as 3 promoções?), devemos averiguar a distribuição dos dados antes escolher qual teste será aplicado. Criamos um histograma das vendas por promoção e podemos ver que há duas distribuições, o que pode afetar a suposição do modelo escolhido. Entretanto, antes de realizar a escolha final, vamos tentar entender o que causa essa distribuição.
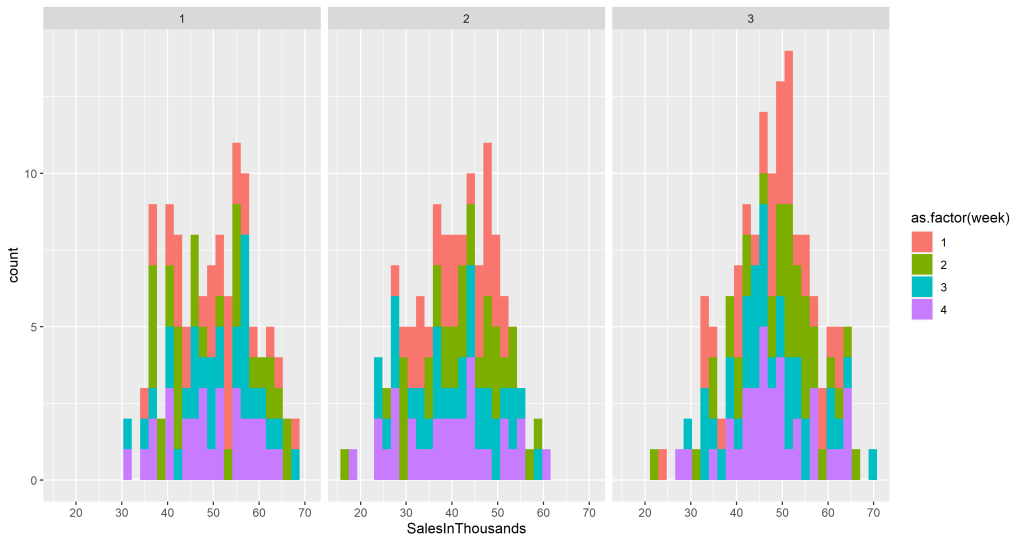
Um fator importante que pode afetar também o número de vendas é o tamanho do mercado. Separamos as distribuições de mercado pequenos e médios. Vemos que já não há mais duas distribuições. Isso nos leva a crer que esse efeito é ocasionado pela distribuição de mercados grandes.
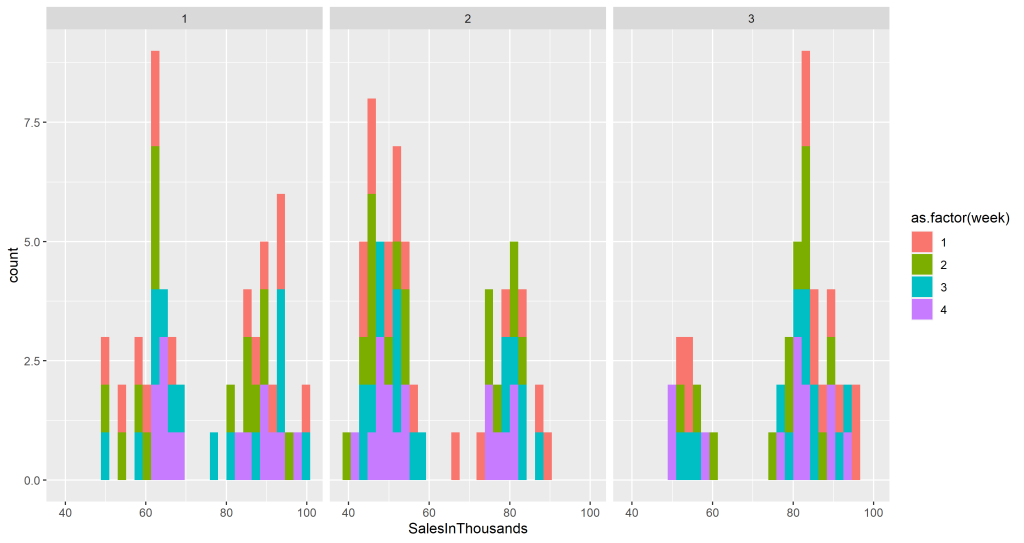
Como dito, ao fazer a separação de mercados grandes, vemos que há duas distribuições. Não iremos nos prolongar com o efeito desse caso, portanto, iremos retirar os mercados grandes do nosso conjunto e apenas tratar de mercados pequenos e médios no nosso exemplo de forma a criar um teste que contém a suposição de distribuição normal (que não testamos, porém, iremos supor da mesma forma).
Podemos realizar a análise acima também com o pacote {skim} em conjunto com group_by(). O interessante é obter as estatísticas descritivas desta forma.
Para testar a hipoteses, vamos utilizar o Teste ANOVA, para verificar se há diferença diferença no valor médio de vendas em mais de dois grupos (as 3 promoções de marketing). Como estabelecido, a variável dependente é SalesInThousand e a variável independente Promotion. Construímos a função aov() com base nessa relação.
No resultado, podemos verificar que o p valor é significativo, ou seja, há significância na promoção de marketing utilizada. Para entender o quanto é essa diferença entre as médias, utilizamos a comparação de Tukey, por meio da função TukeyHSD().
Em diff, obtemos a diferença entre as média dos grupos. lwr e upr os intervalos de confiança e p adj o p valor após os ajuste para comparações múltiplas. Apenas a comparação entre a promoção 3 e 1 não é significativa.
Por fim, podemos avaliar a hipótese criada, levando em conta os mercados analisados. É possível entender que o Teste A/B pode ser extremamente útil para a avaliação de mudanças de programas em empresas, e permite obter resultados bem definidos e claros.