Os modelos de séries temporais univariados permitem a inclusão de informações das observações passadas de uma série, mas não a inclusão de outras informações que possam ser relevantes. Por outro lado, os modelos de regressão múltipla permitem a inclusão de uma grande quantidade de informações relevantes a partir de variáveis preditoras, mas não permitem as dinâmicas sutis de séries temporais que podem ser tratadas com modelos ARIMA. No post de hoje, consideramos estender os modelos ARIMA para permitir que outras informações sejam incluídas nos modelos.
Modelo de Regressão Dinâmico
Modelos de regressão múltipla seguem uma equação do tipo
onde 
e 
são variáveis observáveis e 
é não observável e refere-se a um termo de erro, que supusemos ser um ruído branco.
Podemos agora permitir que apresente autocorrelação. Assim, substituindo por 
e supondo que siga um processo formado por um modelo ARIMA, podemos reescrever a equação acima como
onde 
segue um ruído branco.
Veja que o modelo possui dois termos de erro aqui - o erro do modelo de regressão, que é denotado por e o erro do modelo ARIMA, que é denotado por . Apenas os erros do modelo ARIMA são assumidos como ruído branco.
Estimação com erros ARIMA
Quando estimamos os parâmetros do modelo, precisamos minimizar a soma de valores de quadrados. Se, em vez disso, minimizamos a soma dos valores 
quadrados (o que aconteceria se estimássemos o modelo de regressão ignorando as autocorrelações nos erros), então surgem vários problemas:
- Os coeficientes estimados
não são mais as melhores estimativas, pois algumas informações foram ignoradas no cálculo; - Os testes estatísticos associados ao modelo estão incorretos;
- O AIC dos modelos ajustados não é um bom guia sobre qual é o melhor modelo para a previsão.
- Na maioria dos casos, os
associados aos coeficientes serão muito pequenos e, portanto, algumas variáveis preditoras parecem ser importantes quando não são. Isso é conhecido como regressão espúria.
não são mais as melhores estimativas, pois algumas informações foram ignoradas no cálculo;
associados aos coeficientes serão muito pequenos e, portanto, algumas variáveis preditoras parecem ser importantes quando não são. Isso é conhecido como regressão espúria.Minimizar a soma de valores quadrados de evita esses problemas. Alternativamente, a estimativa da máxima verossimilhança pode ser utilizada; Isso dará estimativas muito semelhantes para os coeficientes.
Uma consideração importante na estimativa de uma regressão com erros ARMA é que todas as variáveis no modelo devem ser estacionárias.
Previsão com erros ARIMA
Para prever um modelo de regressão com erros ARIMA, precisamos prever a parte de regressão do modelo e a parte ARIMA do modelo e combinar os resultados. Tal como acontece com os modelos de regressão ordinários, para obter previsões, precisamos primeiro prever os preditores.
Quando os preditores são conhecidos no futuro (por exemplo, variáveis relacionadas ao calendário, como tempo, dia-semana, etc.), isso é direto. Mas quando os preditores são desconhecidos, devemos modelá-los separadamente ou usar valores futuros assumidos para cada preditor.
Exemplo no R: Consumo e Renda no EUA
Podemos estimar facilmente um modelo de Regressão com erros ARIMA no R utilizando a família de pacotes {tidyverts}, que possibilita criar um framework de criação de modelo de séries temporais. Para exemplificar, usamos as variáveis "personal consumption expenditure" (consumo) e "personal disposable income" (renda) do dataset us_change disponível no pacote {fpp3}, que refere-se a dados de variáveis econômicas do EUA em termos de variação percentual trimestral.
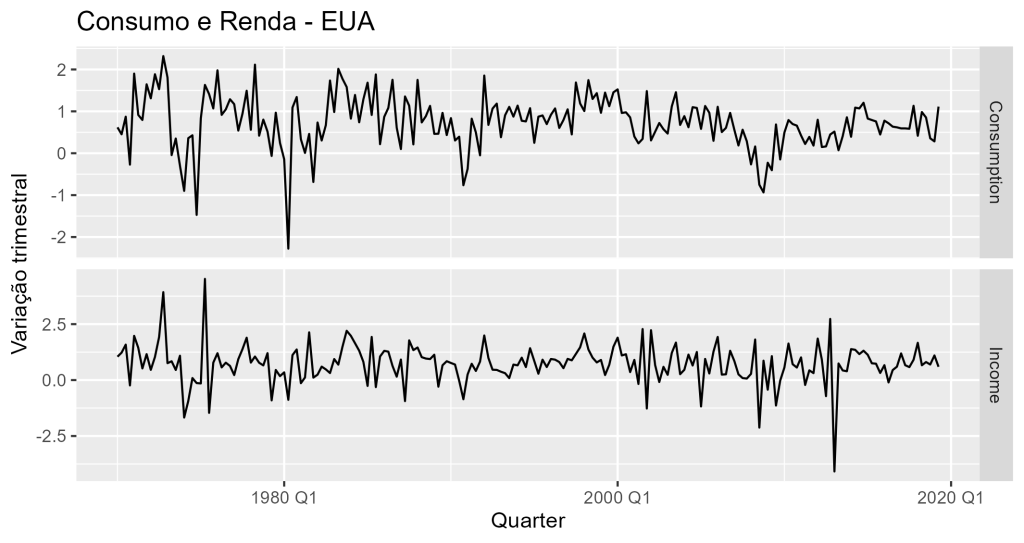
Podemos prever o consumo e usar a renda como uma variável de previsão. Se houver uma queda na renda, podemos esperar que o consumo também caia, e vice-versa. Vejamos a relação de ambas as variáveis:
Vemos que de fato as duas variáveis possuem uma relação contemporânea (é possível verificar que a renda afeta o consumo através de suas defasagens, mas não incluiremos no exemplo). Portanto, podemos utilizar o modelo de regressão dinâmico com erros ARIMA.
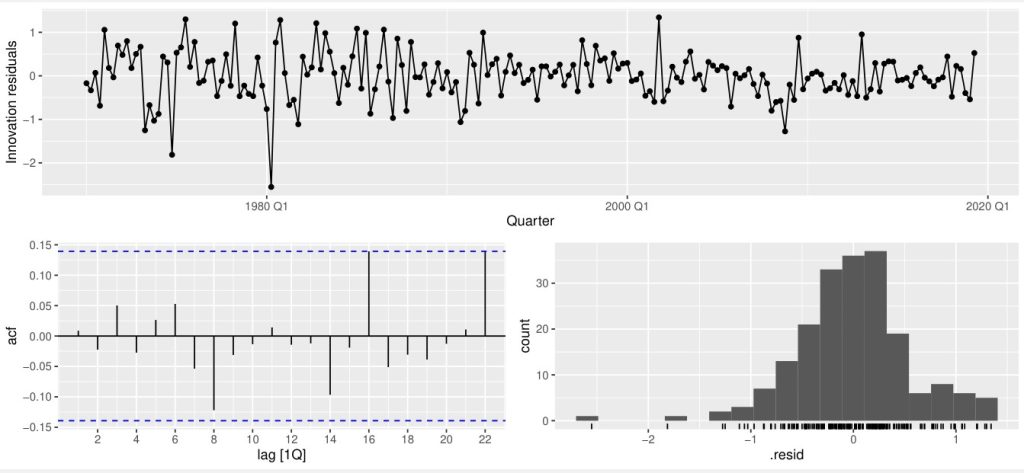
Antes de realizar a previsão, entretanto, devemos verificar se de fato o é um ruído branco:
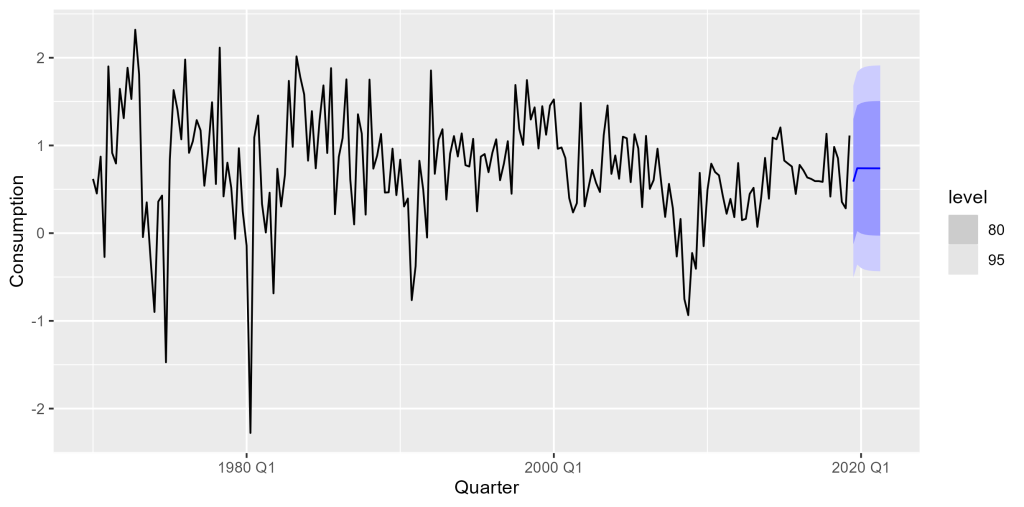
Confirmado a hipótese, podemos partir para a previsão:
________________________________________________
Quer se aprofundar no assunto?
Alunos da trilha de Especialista em Ciência de Dados para Economia e Finanças podem aprender a como construir projetos que envolvem dados reais usando o R e o Python como ferramentas.
Referências
Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-03-07.
