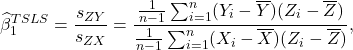Modelos de regressão linear via MQO podem sofrer de diversos problemas, como a omissão de variáveis, erros de mensuração e causalidade simultânea, refletindo na inconsistência dos coeficientes estimados. Como resolver esses problemas? Vamos entender como utilizar variáveis instrumentais para contornar essas questões utilizando um exemplo no R.
O problema da regressão via MQO
O uso de regressão linear podem sofrem de problemas tal como a omissão de variáveis, erros de mensuração e causalidade simultânea, que no geral, fazem que haja correlação entre o termo de erro com o regressor de interesse e que torna o seu respectivo coeficiente inconsistente.
De forma geral, utilizar uma regressão linear múltipla e adicionar mais variáveis pode mitigar o risco da estimação enviesada do modelo, entretanto, há a possibilidade de que essas variáveis omitidas não estejam disponíveis, tanto por motivos de falta de dados, tanto por ser impossível mensura-la (tal como uma variável que represente o talento de uma pessoa).
Outro problema surge caso haja uma causalidade da variável X para Y e vice-versa, causando o viés na estimação do coeficiente.
Variável Instrumental
Uma técnica interessante que dá a possibilidade de contornar esses problemas surge através da regressão de variáveis instrumentais (IV), que possibilita o uso da ferramenta de mínimos quadrados em dois estágios (two-stage least squares - TSLS).
Vamos considerar o seguinte modelo de regressão linear
(1)
Onde o termo de erro u_i é correlacionado com o regressor (X é endógeno) de forma que o MQO seja inconsistente para o verdadeiro
. Na forma mais simples, a regressão IV usa uma única variável instrumental Z para obter o estimador consistente de \beta_i.
Z deve satisfazer duas condições para ser um instrumento válido.
- Condição de relevância: X e seu instrumento Z devem ser correlacionados \rho_{Z_i,X_i} \neq 0
- Condição de exogeinedade do instrumento: o instrumento Z não pode ser correlacionado com o termo de erro u: \rho_{Z_i,u_i} = 0
O estimador de dois estágios por MQO
O TSLS é performado em dois estágios. No primeiro estágio, decompõe-se a variação do regressor endogeno X em um componente, no qual não possui nenhum problema, que é explicado pelo instrumento Z e também em um componente problemático que é correlacionado com o termo de erro \u_i. O segundo estágio utiliza o componente não problemático de X para estimar \beta_i.
O primeiro estágio é
,
onde é o componente de
que é explicado por
enquanto
é o componente que não pode ser explicado por
e é correlacionado com
.
Usando o e
estimado via MQO, obtemos o valores previstos de
. Se Z é um instrumento válido,
não é problemático no sentido em que
é exógeno na regressão de Y em
feita pelo segundo estágio.
O segundo estágio produz (para o caso de um único instrumento)
(2)
Aplicação na demanda por Cigarros
Tomamos como base um exemplo clássico de políticas públicas de saúde, que possuem como finalidade a redução do consumo de cigarros por meio da taxação desses produtos. A questão é saber qual a taxação necessária para que haja uma redução no consumo de cigarros.
Uma solução básica para economistas é usar as elasticidades do produto para responder essa questão. Como entretanto não é conhecido essa elasticidade por demanda do produto, é necessário estimar, e é possível realizar através de dados disponíveis do preço (log) e consumo (log) de cigarros e de uma regressão via MQO para alcançar o objetivo.
O problema ocorre quando encontramos um problema de simultaneadade de causalidade entre a demanda e oferta de cigarro. Para solucionar o problema, é possível utilizar variáveis instrumentais para solucionar o caso.
O dataset CigarettesSW , disponível no pacote {AER}, possui dados que contém observações do consumo de cigarros e outros indicadores economicos dos 48 estado federativos do EUA de 1985a 1995, os dados são disponível na forma de dados em painel.
Para obter o código de importação do dataset, da construção do modelo e também dos códigos subsequentes, faça parte do Clube AM, o repositório especial da Análise Macro.
Utilizando o R, especificamente o pacote a função ivreg do pacote {AER}, conseguimos estimar a seguinte equação
(3)
, tomando como variável instrumental a porção da carga de taxação dos cigarros, obtidos do imposto sobre o consumo.
Como resultado é obtido o seguinte resultado:
________________________________________________
Quer se aprofundar no assunto?
Alunos da trilha de Ciência de dados para Economia e Finanças podem aprender a como construir projetos que envolvem dados reais usando modelos econométricos e de Machine Learning com o R.
Referências
Stock, J.H. e Watson, M.W. (2007). Introduction to Econometrics, 2nd ed. Boston: Addison Wesley.
Hanck, C.; Arnold, M., Gerber, A.; Schmelzer, M.. Introduction to Econometrics with R. Acessado em: "https://www.econometrics-with-r.org/index.html".