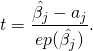Um importante tipo de hipótese que estamos interessados é o da forma em que:
(1)
onde é um número dado [em geral,
]. Para a maioria dos testes bicaudais, a hipótese alternativa implica em:
(2)
e para testes unicaudais, ou temos:
(3)
Essas hipóteses podem ser testadas usando um teste t que é baseado na seguinte estatística:
(4)
Se é verdadeira, essa estatística possui uma distribuição t com
graus de liberdade. Para ilustrar, estimamos uma função para o log do salário-hora. Assim, temos os parâmetros dos retornos percentuais de cada entrada no modelo. Podemos avaliar se, por exemplo, depois de controlar por educação e titularidade, experiência ainda tem um efeito estatisticamente significante no salário-hora.
library(wooldridge)
data("wage1") # puxamos os dados
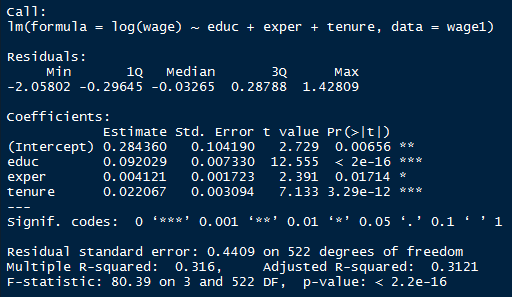
summary(lm(log(wage) ~ educ + exper + tenure, data=wage1))
E abaixo, a saída da regressão.
E de fato, a de significância existe um efeito para experiência. Mais especificamente, um ano a mais de experiência na média se traduz em
de aumento salarial. Observe ainda que a estatística t pode ser calculada como sendo o parâmetro
estimado sobre o erro-padrão. Para o caso da experiência, temos
, que é igual a 2,39. Em outras palavras, podemos rejeitar a hipótese nula que
.
__________________________
(*) Isso e muito mais você aprende em nosso Curso de Introdução à Econometria usando o R.