Séries temporais são conjuntos de dados que são rotulados a cada ponto no tempo. Elas são usadas para entender e prever padrões e tendências ao longo do tempo em muitas áreas, como finanças, meteorologia e saúde pública. No entanto, às vezes as séries temporais podem ser afetadas por mudanças significativas que podem afetar a tendência ou o comportamento dos dados (vide pandemia da Covid-19). Essas mudanças são conhecidas como quebras estruturais.
Causa de quebras estruturais
As quebras estruturais podem ocorrer devido a diversos fatores, como:
- Mudanças na economia
- Alterações nas leis ou regulamentações
- Acontecimentos políticos
- Desastres naturais
- Mudanças tecnológicas
Detecção de quebras estruturais
As quebras estruturais podem ser difíceis de detectar e precisam ser tratadas de maneira especial na análise de séries temporais. Isso é porque elas podem afetar a tendência e a estacionariedade de uma série temporal, além de ser difícil prever como isso pode afetar os dados futuros. No entanto, para detectar quebras estruturais em uma série temporal, é comum usar técnicas de teste de hipóteses ou modelos de decomposição de séries temporais.
Existem vários testes que podem ser usados para detectar quebras estruturais em séries temporais. Alguns dos principais testes incluem:
- Teste de Chow: Este teste verifica se há uma quebra estrutural em uma série temporal dividida em dois períodos. Ele compara os coeficientes de regressão entre os dois períodos e testa se eles são estatisticamente iguais.
- Teste CUSUM e CUSUM-sq: São métodos baseados na ideia de monitorar a soma cumulativa das diferenças entre os valores observados e os valores esperados de uma série temporal. Se essa soma cumulativa atingir um valor crítico, isso pode indicar a presença de uma quebra estrutural.
- Testes sup-Wald, sup-LM e sup-LR: São métodos baseados na ideia de monitorar o valor máximo da diferença entre os valores observados e os valores esperados de uma série temporal em cada período. Se esse valor máximo atingir um valor crítico, isso pode indicar a presença de uma quebra estrutural.
É importante lembrar que nenhum teste é perfeito e que é importante avaliar o contexto e os dados específicos antes de escolher o teste mais adequado para detectar quebras estruturais em uma série temporal. Além disso, é importante levar em consideração as premissas, a significância estatística e outros fatores ao aplicar e interpretar os resultados de qualquer teste de quebra estrutural.
Aplicando testes de quebras estruturais no R
Para aplicar testes de quebra estrutural no R, você pode usar pacotes de análise de séries temporais, como o pacote {strucchange}. Este pacote fornece várias funções para aplicar testes de quebra estrutural em séries temporais, incluindo o teste de Chow, CUSUM e outros.
Por exemplo, para aplicar o teste de Chow para identificar todos as possíveis quebras estruturais de uma série temporal, existe a função "Fstats()". Essa função calcula várias estatísticas F (a estatística do teste de Chow) para uma dada série temporal. O resultado pode então ser usado para testes de hipóteses através da função "sctest()", onde a hipótese nula é de ausência de quebra estrutural. A partir disso um nível de significância deve ser escolhido para determinar pela rejeição ou não da hipótese nula baseando-se no p-valor calculado pela função.
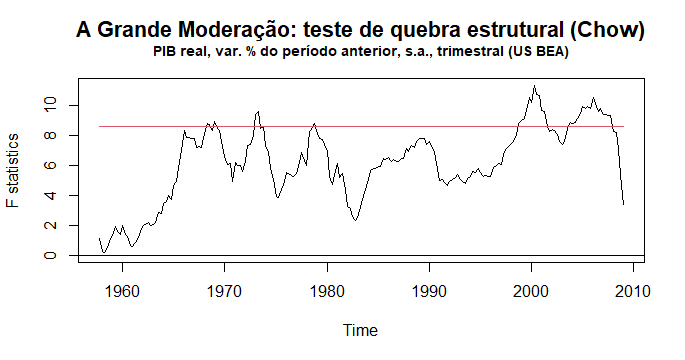
Ainda é possível com o pacote {strucchange} fazer a análise gráfica dos resultados com a função "plot()", que apresenta a série temporal das estatísticas F contra uma linha de fronteira. Quando a série ultrapassa a fronteira, há evidências de que há quebras estruturais nos dados originais sendo testados.
O pacote {strucchange} é de fácil instalação e está disponibilizado pelo repositório CRAN.
Saiba mais
Para se aprofundar no assunto confira o curso de Análise de Séries Temporais e para ver exemplos práticos e códigos de reprodução em R e Python, faça parte do Clube AM da Análise Macro.