Previsão de demanda com o Prophet usando Python

Introdução

Prophet é um modelo de previsão desenvolvido pelo Facebook em 2017 que promete entregar previsões em escala. É ideal para séries temporais com forte sazonalidade e com muitas observações de dados. Ele é baseado em um modelo aditivo ajustado com tendências não lineares, sazonalidades e efeitos de feriado, além de ser robusto a valores ausentes, mudanças de tendência e valores extremos.

Nesse artigo apresentamos o modelo Prophet, através da decomposição das equações e parâmetros, e mostramos um exemplo aplicado com dados para previsão de demanda usando as linguagens de programação R e Python.

Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.

Modelo de previsão Prophet

O Prophet foi desenhado pela equipe do Facebook para solucionar os seguintes problemas em um contexto de tarefas de previsão de séries temporais em ambiente empresarial, conforme Taylor e Letham (2017):

Um grande número de pessoas produzindo previsões, possivelmente sem treinamento técnico aprofundado;
Um grande número de tarefas de previsão, possivelmente com particularidades únicas;
Uma demanda por um sistema de previsão automatizado, veloz, eficiente.

Existem muitas séries temporais em ambiente empresarial para as quais é necessário produzir previsão, ao mesmo tempo que é preciso superar os problemas destacados acima. Felizmente, existem algumas características em comum para grande parte dessas séries temporais.

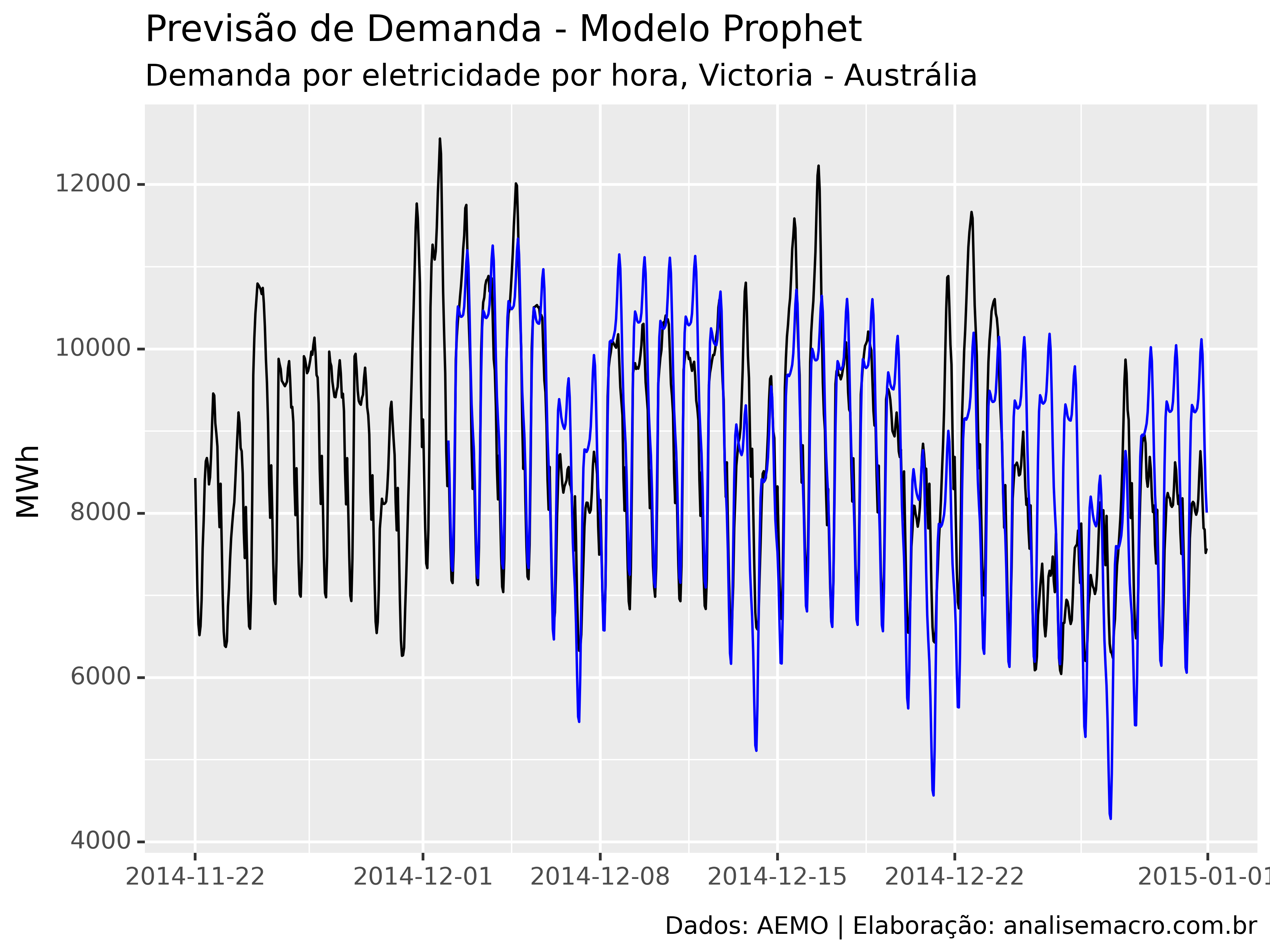
Por exemplo, veja esses dados de demanda por eletricidade por hora na cidade de Victoria na Austrália (fonte Australian Energy Market Operator):

Essa série temporal mostra claramente algumas características:

Ciclos sazonais anuais e horários
Aumentos repentinos em grandes feriados (final de ano)
Valores extremos

Para lidar com essas características comuns em séries temporais o Prophet utiliza um modelo de decomposição, da seguinte forma:

$y_t = T_t + S_t + F_t + \epsilon_t$

onde:

$y_t$ é a série temporal alvo de previsão;

$T_t$ é o componente de tendência que modela variações não periódicas de $y_t$ ;

$S_t$ é o componente de sazonalidade que modela variações periódicas de $y_t$ ;

$F_t$ é a representação de efeitos de feriados e eventos sobre $y_t$ ;

$\epsilon_t$ é o termo de erro que representa variações idiossincráticas, assumido como normalmente distribuído.

A seguir descrevemos o procedimento de modelagem de cada componente no modelo Prophet.

Componente de tendência do Prophet

O componente de tendência do modelo Prophet pode ser representado de duas formas:

Tendência com crescimento não linear e saturanteA ideia é que a tendência possui um crescimento não linear que "satura" uma capacidade de carga. Por exemplo, a capacidade de carga da demanda por eletricidade de uma cidade pode ser o número de dispositivos que consomem eletricidade. Esse tipo de crescimento no Prophet é dado por uma função de crescimento logístico por partes, permitindo pontos de

$T_t = \frac{C_{t}}{1 + \exp(-(k + a_t^T\delta)(t - (m + a_t^T\gamma)))}$

onde:

$C_t$ é a capacidade de carga variante no tempo;

$k$ é uma taxa básica de crescimento da tendência;

$a_{t}^T$ é uma taxa de ajuste da taxa básica de crescimento, sendo $a_t$ igual a 1 se $t$ for maior ou igual ao $j$ ponto de mudança e igual a zero caso contrário;

$\delta$ é a mudança da taxa de ajuste que ocorre no $j$ ponto de mudança;

$m$ é um parâmetro de deslocamento;

$\gamma$ é a correção do ajuste no $j$ ponto de mudança.

Os pontos de mudança podem ser definidos a priori utilizando datas conhecidas sobre a série temporal ou podem ser automaticamente selecionados.

Tendência com crescimento linear com pontos de mudançaA ideia dessa versão do componente de tendência é quando a série temporal não possui comportamento "saturante" da capacidade de carga, portanto uma taxa constante de crescimento é aplicável:

$T_t = (k + a_t^T\delta)t + (m + a_t^T\gamma)$

Componente de sazonalidade do Prophet

O componente de sazonalidade do modelo Prophet é representado da seguinte forma:

$S_{t} = \sum_{n=1}^N \left (a_{n} \cos \left ( \frac{2 \pi n t}{P} \right ) + b_n \sin \left (\frac{2 \pi n t}{P} \right) \right )$

onde:

$a$ e $b$ são os parâmetros sazonais a serem estimados, assumidos como normalmente distribuídos;

$P$ é a periodicidade regular da série (i.e., $P=7$ para séries semanais).

A ideia por trás desse componente é que a série temporal pode ter múltiplas sazonalidades, como resultado do comportamento humano. Por exemplo, uma jornada de trabalho de 5 dias por semana pode produzir efeitos em uma série temporal que se repetem semanalmente, enquanto que férias escolares e outros podem produzir efeitos que se repetem anualmente.

Componente de feriados e eventos do Prophet

Feriados e eventos podem produzir um grande efeito sobre uma série temporal sem um padrão periódico. Por exemplo, o evento Rock in Rio acontece na cidade do Rio de Janeiro a cada 2 anos aproximadamente. Já a Páscoa ocorre no primeiro domingo depois da lua cheia após o início do equinócio de verão. Os efeitos destes feriados e eventos nas séries temporais costumam ser similares ano após ano, dessa forma é importante incorporá-los no modelo de previsão.

No modelo Prophet, os efeitos de feriados e eventos são incorporados adicionando uma matriz $Z_t$ de variáveis independentes que assumem o valor 1 se a observação no tempo $t$ é durante o feriado/evento e multiplicando por um parâmetro $\kappa$ para representar a mudança na previsão. Dessa forma, temos que:

$F_{t} = Z_{t} \kappa$

onde:

$\kappa$ é assumido como normalmente distribuído.

O modelo é estimado usando a máxima probabilidade a posteriori (MAP), da estatística bayesiana, através da linguagem Stan.

Exemplo aplicado do modelo Prophet: previsão de demanda

Agora vamos mostrar como utilizar o modelo Prophet para previsão, usando como exemplo os dados exibidos acima da demanda por eletricidade por hora na cidade de Victoria na Austrália (fonte Australian Energy Market Operator).

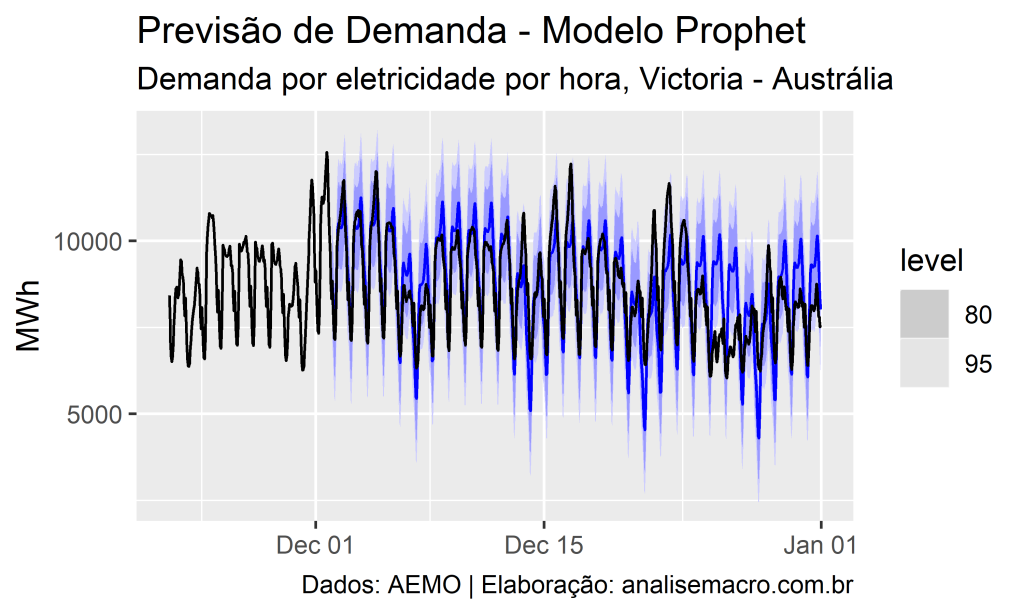
Abaixo reportamos (a) as métricas de acurácia de treino/teste e (b) o gráfico de valores observados e previsão fora da amostra.

RMSE de treino: 940.9689553290613
RMSE de teste: 913.6017458369588

Note que o modelo gera previsões que estão, analisando apenas os resultados acima, se generalizando bem.

A linha preta no gráfico mostra os dados observados, enquanto que a linha azul mostra a previsão fora da amostra.

Note que avaliar pontos de previsão sem levar em consideração o intervalo de confiança pode esconder uma grande incerteza e levar a conclusões errôneas.

Considerações

Quer aprender mais?

Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.

Referências

Taylor SJ, Letham B. 2017. Forecasting at scale. PeerJ Preprints 5:e3190v2 https://doi.org/10.7287/peerj.preprints.3190v2

Prophet: Automatic Forecasting Procedure https://pypi.org/project/prophet/

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Previsão de demanda com o Prophet usando Python

Como choques inflacionários afetam a previsão da Selic?

Modelo de previsão para o preço da gasolina

Como construir um Vetor Autoregressivo Estrutural (SVAR) no Python?

Previsão com Vetores Autoregressivos no Python

Previsão do Desemprego: Redes Neurais vs. Previsões do Focus

Outros artigos relacionados

Previsão de demanda com o Prophet usando Python

Apresentamos o modelo Prophet e mostramos um exemplo aplicado com dados para previsão de demanda usando Python.

Como choques inflacionários afetam a previsão da Selic?

Como mensurar a importância de choques na inflação sobre o erro de previsão da taxa de juros? Neste exercício quantificamos esta pergunta sob a ótica de um modelo VAR, usando dados recentes da macroeconomia brasileira. Especificamente, estimamos a decomposição da variância dos erros de previsão do modelo, analisando choques na inflação da gasolina e sua importância sobre a variância dos erros de previsão da taxa Selic.

Modelo de previsão para o preço da gasolina

Neste exercício exploramos os dados públicos sobre o preço da gasolina no Brasil, sua composição, evolução temporal, políticas associadas e, por fim, construímos um modelo simples de previsão. Com um modelo em mãos, o analista pode cenarizar o comportamento futuro da série da forma como preferir. Todos os procedimentos foram feitos usando a linguagem de programação Python.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!