A regressão de dados em painel é uma técnica estatística usada para analisar dados longitudinais, ou seja, dados coletados ao longo do tempo de uma mesma unidade de análise, como empresas, indivíduos ou países. Essa técnica é muito útil para modelar a relação entre variáveis dependentes e independentes, controlando o efeito de outras variáveis que possam influenciar a relação. Neste post, exploraremos as principais funcionalidades do Python para análise de regressão em painel e como aplicá-las.
Regressão com dados em painel
regressão de dados em painel é uma técnica estatística usada para analisar dados longitudinais que consistem em observações repetidas ao longo do tempo de uma mesma unidade de análise. Essa técnica é baseada em modelos de efeitos fixos, que capturam a heterogeneidade inobservada entre as unidades de análise, e modelos de efeitos aleatórios, que assumem que as unidades de análise são selecionadas aleatoriamente de uma população mais ampla.
As principais vantagens da regressão em painel incluem a
- redução de erros de estimação;
- a eliminação de variáveis que não variam ao longo do tempo;
- evitar a multicolinearidade;
- a possibilidade de avaliar os efeitos de políticas ou tratamentos ao longo do tempo.
Além disso, a regressão em painel permite controlar o efeito de outras variáveis que possam influenciar a relação entre as variáveis dependentes e independentes.
Efeitos Fixos
Os efeitos fixos na regressão de dados em painel referem-se a variáveis que variam entre as unidades de análise (indivíduos, empresas, países, etc.) e que são constantes ao longo do tempo. Essas variáveis são incluídas no modelo para controlar a heterogeneidade entre as unidades de análise que não pode ser observada ou medida.
Em outras palavras, os efeitos fixos permitem capturar diferenças não observáveis entre as unidades de análise que podem influenciar a relação entre as variáveis dependentes e independentes. Isso pode ajudar a melhorar a precisão das estimativas e reduzir os erros de estimação.
Os efeitos fixos são estimados incluindo variáveis dummy no modelo, que representam cada unidade de análise. Cada dummy é codificada como 1 para a unidade de análise correspondente e 0 para as outras unidades de análise. Isso permite que o modelo capture as diferenças não observáveis entre as unidades de análise, controlando seu efeito sobre a relação entre as variáveis dependentes e independentes.
Os efeitos fixos também são conhecidos como modelos de efeitos individuais ou modelos de intercepto aleatório. Eles são amplamente utilizados em pesquisas que envolvem dados longitudinais ou em estudos comparativos entre unidades de análise que diferem em suas características não observáveis.
Geralmente, o modelo de efeito fixo é definido como:
onde é o resultado do individuo i no tempo t.
é o vetor de variáveis dos indivíduos i no tempo t.
é o conjunto não observável do individuo i. Observe que esses inobserváveis são imutáveis ao longo do tempo, daí a falta do subscrito de tempo. Finalmente,
é o termo de erro.
Exemplo
Vamos verificar a aplicação do dados usando o dataset wage_panel, disponível na biblioteca linearmodels, referente ao trabalho de Vella e Verbeek (1998). A ideia do artigo é responder a seguinte pergunta: Homens casados são mais ricos?
Para obter o código de importação do dataset, da construção do modelo e também dos códigos subsequentes, faça parte do Clube AM, o repositório especial da Análise Macro.
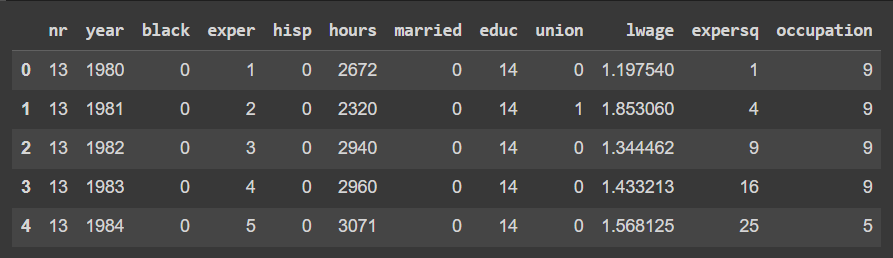
No dataset, temos diversas variáveis que podem auxiliar na explicação no salário. Etnicidades, horas trabalhadas, educação, expertise (anos trabalhados) e ocupação.
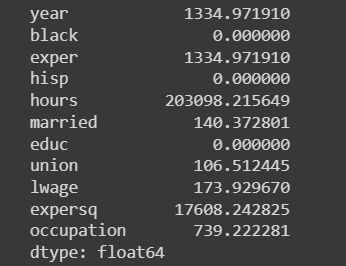
Para aplicar a regressão com dados em painel, vamos retirar as variáveis dummys que são constantes. As variáveis que são constantes no tempo são uma combinação linear dos dummys, o que faz com que o modelo não rode.
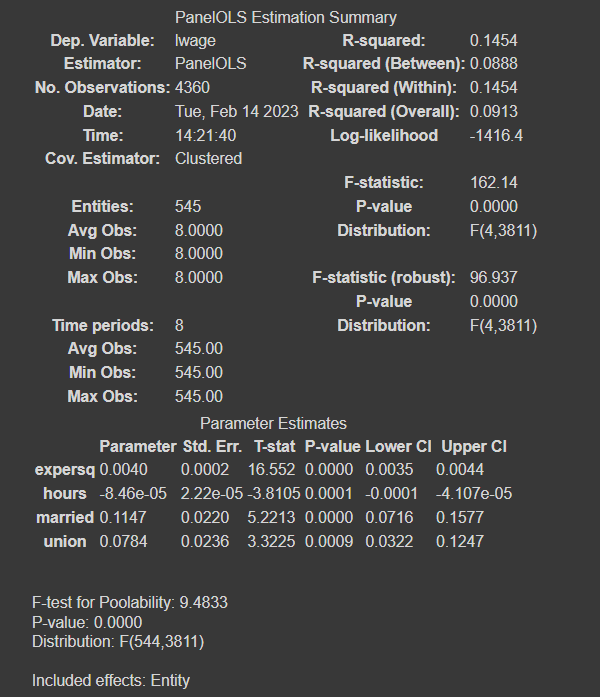
Agora, podemos aplicar a regressão a partir das variáveis que não são constantes, também não usaremos a variável occupation, pois pode estar mediando o efeito de marriage em wage (casamento sobre o salário). Usaremos a biblioteca linearmodels, que possui a função PanelOLS. Como resultado, teremos:
Como resultados, verificamos o efeito de que o casamento provoca o aumento de 11% sobre o salário.
Referências
Vella and M. Verbeek (1998), “Whose Wages Do Unions Raise? A Dynamic Model of Unionism and Wage Rate Determination for Young Men,” Journal of Applied Econometrics 13, 163-183.