Cross Validation ou Validação Cruzada é um método que permite avaliar a performance preditiva de um modelo de previsão, podendo este ser um modelo de séries temporais. No post de hoje, vamos analisar, por meio da validação cruzada, o poder preditivo de modelos univariados da inflação mensal utilizando o Python.
Cross Validation
Na criação de modelos estatísticos usados com a finalidade de previsão há sempre a preocupação de seu poder preditivo. Para tanto, existe o famoso método de separar os dados em uma amostra de treino e teste e verificar como a previsão dos dados de treino se comparam com o de teste.
Entretanto, para facilitar o uso deste tipo de método, há o uso do Cross Validation, em que uma série de amostras de teste, cada uma consistindo em h observações, ou seja, são os períodos usados para gerar previsões a partir do modelo. A amostra de treino correspondente, usada para estimação do modelo, consiste apenas de observações que ocorreram antes das observações que formam a amostra de teste. Assim, nenhuma observação futura pode ser usada na construção da previsão.
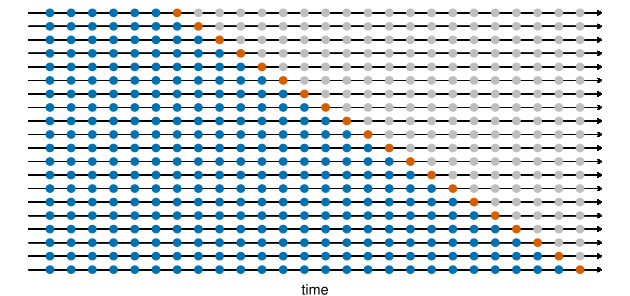
O diagrama a seguir ilustra um esquema de validação cruzada de séries temporais, com uma série de amostras de treino e de teste, para quando se deseja avaliar a performance preditiva do modelo em h = 1 períodos à frente, onde as observações azuis formam as amostras de treino e as observações laranja formam as amostras de teste.
Aplicação no Python
Vamos criar um exercício para aplicar o Cross Validation em modelos univariados de séries temporais utilizando o Python. Para isso, seguiremos os seguintes passos:
- Importação e tratamento da variação mensal do IPCA;
- Criação e operacionalização dos modelos univariados com a biblioteca statsforecast - AutoArima; AutoETS; AutoCES e AutoTheta.
- Aplicação do Cross Validation.
Portanto, começaremos carregando as bibliotecas e os modelos univariados utilizados no exemplo.
from bcb import sgs import matplotlib.pyplot as plt import numpy as np import pandas as pd from statsforecast import StatsForecast from statsforecast.models import ( AutoARIMA, AutoETS, AutoCES, AutoTheta )
Após a importação das bibliotecas, coletamos os dados do IPCA mensal através do SGS do Banco Central utilizando o código 433. Os dados são após 2004.
# Coleta do IPCA
ipca_raw = sgs.get(('y', 433), start = '2004-01-01')
# Tratamento do IPCA
ipca = (
ipca_raw
.reset_index()
.assign(unique_id = 'ipca')
.rename(columns = {'Date' : 'ds' })
)
<pre>
Agora, criaremos todos os modelos com base nos dados importados do IPCA. Nesse caso, não iremos repartir em amostras de treino e teste.
# Seleciona seis modelos models = [ AutoARIMA(season_length = 12), AutoETS(12), AutoCES(12), AutoTheta(12) ] # Roda os modelos sf = StatsForecast( df = ipca, models = models, freq = 'M', n_jobs = -1 ) # forecast forecasts_df = sf.forecast(h = 12, level=[90])
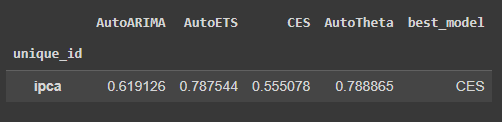
Com os modelos criados, utilizaremos o objeto sf e o método cross_validation para aplicar a Validação Cruzada nos dados. O resultado será avaliado por RMSE e o melhor modelo será escolhido por meio de uma função criada abaixo.
</pre> # Roda o cross validation crossvalidation_df = sf.cross_validation( df = ipca, h = 12, step_size = 1, n_windows = 1 )
from datasetsforecast.losses import mse, mae, rmse def evaluate_cross_validation(df, metric): models = df.drop(columns=['ds', 'cutoff', 'y']).columns.tolist() evals = [] for model in models: eval_ = df.groupby(['unique_id', 'cutoff']).apply(lambda x: metric(x['y'].values, x[model].values)).to_frame() # Calculate loss for every unique_id, model and cutoff. eval_.columns = [model] evals.append(eval_) evals = pd.concat(evals, axis=1) evals = evals.groupby(['unique_id']).mean(numeric_only=True) # Averages the error metrics for all cutoffs for every combination of model and unique_id evals['best_model'] = evals.idxmin(axis=1) return evals evaluation_df = evaluate_cross_validation(crossvalidation_df, rmse)
O melhor modelo resultante pela função foi o AutoCES, no qual será utilizado para realizar o forecast do IPCA.
</pre>
fig, ax = plt.subplots(1, 1, figsize = (20, 7))
plot_ipca = ipca.set_index('ds')
plot_ipca[['y']].plot(ax = ax, linewidth=2)
plot_y_hat = forecasts_df.set_index('ds')
plot_y_hat[['CES']].plot(ax = ax, linewidth=2)
ax.set_title('Previsão IPCA - AutoCES', fontsize=22)
ax.set_ylabel('IPCA %a.m', fontsize=20)
ax.legend(prop={'size': 15})
ax.grid()
<pre>
________________________________________________
Quer se aprofundar no assunto?
Alunos da trilha de Ciência de dados para Economia e Finanças possuem acesso o curso Analise de dados Macroeconômicos e Financeiros e podem aprender a como construir projetos que envolvem dados reais usando modelos econométricos e de Machine Learning com o R.
Referências
Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on <2022-05-12>.