Estacionariedade de Séries Temporais no Python

Uma série temporal é uma sequência de observações organizadas em função do tempo, ou seja, uma sequência de valores coletados ao longo do tempo Cada observação representa a medição de uma variável aleatória em um instante específico .

Por exemplo, a série da taxa de desocupação é uma série temporal, pois seus valores seguem uma ordem cronológica. O mesmo se aplica a diversas séries econômicas e financeiras.

Para realizar análises, modelagens e previsões confiáveis, é essencial que a série seja estacionária. A estacionariedade garante previsões mais precisas e parâmetros estatísticos mais bem comportados, facilitando a interpretação e aplicação dos modelos.

Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.

Estacionariedade

Estacionariedade de uma série temporal é uma propriedade importante que descreve como seus valores estatísticos se comportam ao longo do tempo. Uma série temporal é considerada estacionária se suas propriedades estatísticas (como a média, a variância, a autocovariância) não mudam ao longo do tempo.

A estacionariedade fraca de uma série temporal é quando a média e a variância da série são constantes ao longo do tempo, mas a autocovariância (covariância entre observações em diferentes pontos no tempo) pode depender da distância entre as observações e do tempo específico em que elas ocorrem.

Um processo estocástico é dito fraca ou fracamente estacionário se suas propriedades estatísticas básicas são invariantes ao longo do tempo. Formalmente, um processo estocástico é considerado fracamente estacionário se:

1. A média é constante para todos os tempos .
2. A autocovariância depende apenas da diferença temporal , ou seja, para todo , e .

Já a estacionariedade forte de uma série temporal é quando todas as propriedades estatísticas, incluindo a média, a variância e a autocovariância, são constantes ao longo do tempo. Esse é um tipo mais rigoroso de estacionariedade e é geralmente necessário para aplicar muitas técnicas estatísticas e de modelagem em séries temporais.

Em outras palavras, se a média e a variância dos dados permanecerem constantes ao longo do tempo e a autocovariância (covariância entre observações em diferentes pontos no tempo) depender apenas da distância entre as observações e não do tempo específico em que elas ocorrem, a série temporal é considerada estacionária.

A estacionariedade é importante porque muitos modelos estatísticos e técnicas de análise de séries temporais dependem dessa propriedade para serem aplicados com eficácia. Além disso, a detecção de mudanças na estacionariedade de uma série temporal pode ser útil na identificação de pontos de mudança significativa no processo que está sendo monitorado.

Série Temporais Econômicas

Uma série temporal estacionária é aquela cujas propriedades estatísticas (média, variância, etc.) não dependem do tempo em que a série é observada. Sendo assim, séries com tendências ou com sazonalidade não são estacionárias - a tendência e a sazonalidade afetarão o valor da série temporal em momentos diferentes. Já uma série de ruído branco (white noite) é estacionária - não importa a janela amostral observada, deve parecer sempre o mesmo padrão em qualquer momento.

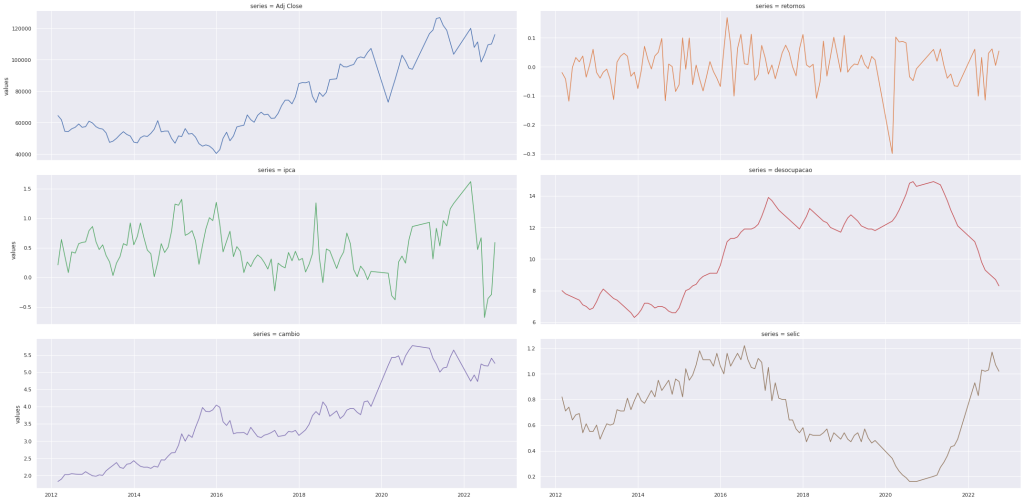
Vejamos algumas séries temporais. Temos abaixo as séries mensais: Ibovespa, retornos da Ibovespa, IPCA, Desocupação, Câmbio e Selic, respectivamente.

Os gráficos mostram de forma bem clara fortes tendências nas séries da taxa de câmbio, taxa de desocupação e taxa SELIC, enquanto que a série da inflação medida pelo IPCA possui aspecto parecido com uma série estacionária. Já a série do Ibovespa aparenta ser um random walk, enquanto os retornos da Ibovespa aparentam ser uma série estacionária.

Entretanto, como avaliar as séries de forma a ter evidencia de que fato elas são estacionárias? Podemos fazer isso por meio de testes estatísticos criados com esse propósito.

Raiz Unitária

A raiz unitária é uma propriedade de séries temporais que indica a presença de uma raiz da equação característica igual a 1, o que pode levar a um comportamento não estacionário da série temporal. Em termos mais simples, a presença de uma raiz unitária sugere que a série temporal não é estacionária ou que sua média e variância mudam com o tempo. É possível avaliar se há a presença de raiz unitária em uma série pode meio de dois teste.

Augmented Dickey Fuller (“ADF”)

O Teste ADF é usado para determinar a presença de raiz unitária nas séries, e portanto, verificar se a série é estacionária ou não.

No teste, a hipótese nula e a hipótese alternativa são:

• Hipótese Nula: a série contém raiz unitária
• Hipótese Alternativa: a série não contém raiz unitária

Se não rejeitarmos a hipótese nula, o teste evidencia que a série não é estacionária.

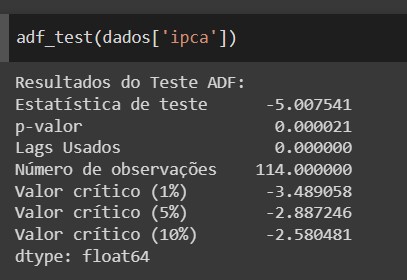
O Teste ADF no Python, usando a biblioteca statsmodels, provê os seguintes resultados: - estatística de teste, p-valor e valor crítico em 1%, 5% e 10% de intervalos de confiança. Abaixo, vejamos a aplicação na série do IPCA.

Acima, vemos que o teste rejeita H0, portanto, a série é dita estacionária.

Kwiatkowski-Phillips-Schmidt-Shin (“KPSS”)

O KPSS é outro teste para checar se a série é estacionária. As hipóteses do KPSS são o oposto do ADF, isto é:

• Hipótese Nula: a série não contém raiz unitária
• Hipótese Alternativa: a série contém raiz unitária

Se não rejeitarmos a hipótese alternativa, o teste evidencia que a série não é estacionária.

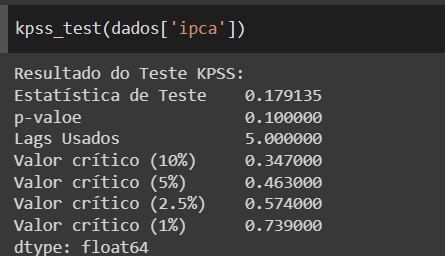
O Teste KPSS no Python, usando a biblioteca statsmodels, provê os seguintes resultados: - estatística de teste, p-valor e valor crítico em 1%, 5% e 10% de intervalos de confiança. Abaixo, vejamos a aplicação na série do IPCA.

O Teste não rejeita H0, portanto, a série é dita estacionária.

É sempre sugerido aplicar ambos os testes nas séries, de forma que se possa confirmar com total certeza de que as séries são realmente estacionárias. Há ainda os possíveis resultados dos testes:

1. Caso 1: Ambos os testes concluem que a série não é estacionária - A série não é estacionária
2. Caso 2: Ambos os teste concluem que a série é estacionária - A série é estacionária
3. Caso 3: KPSS indica estacionariedade, e ADF indica não estacionariedade. A série possui tendência estacionária, portanto, é necessário remover a tendencia para que a série seja estritamente estacionaria. Verifica-se se a nova série é estacionária.
4. Caso 4: KPSS indica não estacionariedade e ADF indica estacionariedade. A série é estacionária na diferença, ou seja, é necessário diferenciar a série para que ela seja estacionária. Verifica-se se a nova série é estacionaria.

________________________________________________

Quer aprender mais?

Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.

Referências

Forecasting: Principles and Practice Hyndman, R. & Athanasopoulos, G., 2021, 3rd ed. OTexts. Recuperado em https://otexts.com/fpp3/