Em termos simples, classificadores nearest neighbor - vizinho mais próximo - são definidos pela sua característica de classificar exemplos não rotulados atribuindo a eles a classe de exemplos rotulados similares. A despeito dessa definição simples, os métodos nearest neighbor são extremamente poderosos. Eles têm sido bem sucedidos em:
- Reconhecimento facial em vídeos e imagens;
- Prever se uma pessoa irá gostar de um filme ou música recomendada;
- Identificar padrões em dados genéticos.
Em geral, classificadores nearest neighbor são bem adequados para tarefas de classificação.1
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
O algoritmo k-NN
O método de nearest neighbor para classificação é exemplificado pelo algoritmo k-nearest neighbor (k-NN). Embora seja um dos mais simples algoritmos de ML, ele ainda é bastante utilizado. A seguir os pontos fortes e fracos dessa abordagem:
Pontos fortes:
- Simples e efetivo;
- Não faz suposição sobre a distribuição dos dados;
- Fase de treino rápida.
Pontos fracos:
- Não há produção de modelo;
- Requer a seleção de um k apropriado;
- Fase de classificação lenta;
- Características nominais e missing data requerem processamento adicional.
O algoritmo k-NN tem esse nome do fato de que ele usa informação de um exemplo k-nearest neighbors para classificar exemplos não rotulados. A letra k é um termo variável implicando que qualquer número de vizinhos próximos pode ser utilizado.
Após escolher k, o algoritmo requer um dataset de treino contendo exemplos que são classificados em diferentes categorias, rotulados por uma variável nominal. Assim, para cada registro não rotulado no dataset de teste, o algoritmo k-NN identifica k registros no dataset de treino que estão mais próximos em similaridade. O exemplo de teste não rotulado é então atribuído à classe da maioria dos k vizinhos mais próximos.
Para ilustrar, vamos considerar uma experiência de jantar às escuras. Suponha que antes do jantar, nós tenhamos criado um dataset que nossa impressão sobre um número de ingredientes previamente experimentados. A seguir as primeiras linhas do dataset:
| Ingrediente | Doçura | Crocância | Tipo |
|---|---|---|---|
| bacon | 1 | 4 | proteína |
| banana | 10 | 1 | fruta |
| cenoura | 7 | 10 | vegetal |
| alface | 2 | 10 | vegetal |
| queijo | 1 | 1 | proteína |
| uva | 8 | 5 | fruta |
| feijão | 3 | 7 | vegetal |
| nozes | 3 | 6 | proteína |
| laranja | 7 | 3 | fruta |
De modo a manter as coisas simples, nós rotulamos os ingredientes a partir de duas características: crocância e doçúra. Assim, o algoritmo k-NN irá tratar essas características como coordenadas em espaço multidimensional.

Observe que os tipos similares de frutas tendem a ser agrupadas próximas uma das outras, considerando as características que marcamos.
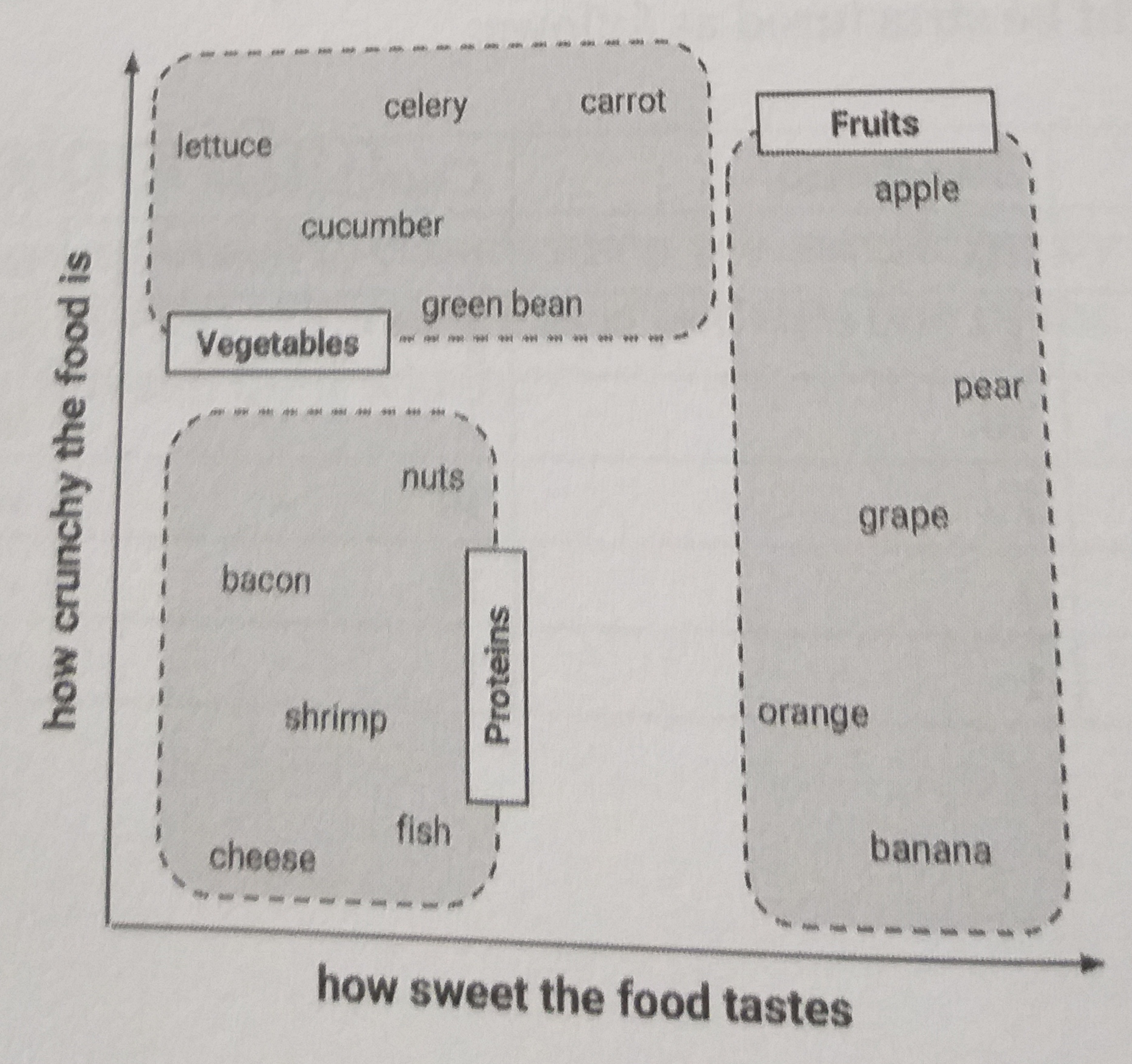
Uma vez construído nosso dataset, podemos usá-lo para decidir se uma tomate é uma fruta ou vegetal.
Medindo similaridade com distância
Localizar o vizinho mais próximo da tomate requer uma função de distância ou uma fórmula que meça a similaridade entre dois exemplos.
Existem várias maneiras de calcular distância. Tradicionalmente, o algoritmo k-NN utiliza a distância euclidiana.
A distância euclidiana é especificada pela fórmula:
Onde e
são os exemplos a serem comparados, cada um possuindo
características. No nosso exemplo,
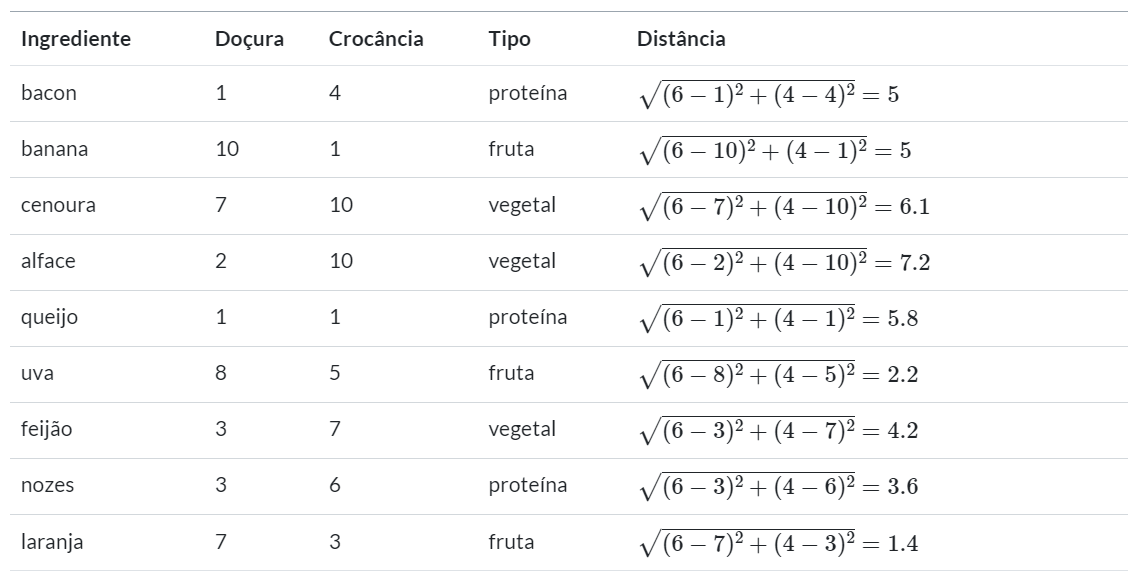
A seguir, calculamos a distância para o tomate de outros vizinhos próximos:
Para classificar a tomate como vegetal, proteína ou fruta, nós começamos por atribuir ao tomate o tipo de alimento do seu vizinho mais próximo. Isso é chamado de classificação 1-NN porque . Na tabela acima,
orange é o vizinho mais próximo do tomate, com uma distância de 1.4. Como orange é uma fruta, o tomate é classificado também como fruta.
Se nós utilizamos , nós performamos um voto através dos três vizinhos mais próximos:
orange, grape e nuts. Dado que a maioria desses ingredientes pertence à classe fruta, nós de novo classificamos o tomate como fruta.
Escolhendo um k apropriado
A decisão de quantos vizinhos usar para o algoritmo k-NN determinará quão bem o modelo irá gerar os dados futuros. O balanço entre overfitting e underfitting o dataset de treino é um problema conhecido como bias-variance tradeoff.2
o tradeoff de viés e variância é a propriedade de um conjunto de modelos preditivos em que os modelos com um viés menor na estimativa de parâmetros têm uma variância maior das estimativas de parâmetros entre as amostras e vice-versa.
A escolha de um k alto, nesse contexto, reduz o impacto ou variância causada por dados que sejam ruídos, mas pode viesar o aprendizado. Por outro lado, utilizar um único vizinho mais próximo permite que dados ruidosos ou outliers influenciem a classificação de exemplos. O melhor valor para k, portanto, será algo entre esses dois extremos.
Uma prática comum é escolher como sendo a raíz quadrada do número de exemplos contidos no dataset de treino.3
Exemplo de k-vizinhos mais próximos: classificação econômica
Nessa seção apresentamos um exemplo do algoritmo k-vizinhos mais próximos.
O problema que utilizaremos nesse exemplo é o seguinte:
- Deseja-se distinguir os países do mundo, em termos de desempenho econômico, em 3 categorias: economias avançadas, economias emergentes e economias de baixa renda.
- A finalidade da classificação é informacional: é mais fácil analisar e comparar o desempenho econômico de países dentro de uma mesma economia, além de servir como insumo para outros tipos de classificação, como, por exemplo, o risco de crédito soberano.
Os dados utilizados para abordar esse problema são os seguintes:
- Agrupamento econômico do Monitor Fiscal do IMF: consiste de uma classificação oficial, de uma instituição reconhecida internacionalmente, que agrupa os países do mundo em 3 grandes categorias (41 avançadas, 95 emergentes e 59 renda baixa). Esses dados formam a variável de interesse Y do nosso problema de classificação. Essas informações estão disponíveis neste link do IMF, onde há esse outro link para uma planilha de Excel com os agrupamentos e outros metadados.
- Produto Interno Bruto (PIB): consiste na variável utilizada pelo IMF, conforme o Methodological and Statistical Appendix do Monitor Fiscal4, para agrupar as economias pelo tamanho do PIB em dólares americanos. Esses dados, sendo o valor anual de 2018 divulgado para cada país no conjunto de dados WEO a referência aqui utilizada, formam a variável independente X do nosso problema de classificação. Essas informações estão disponíveis na base de dados DBnomics.
Nota: os links acima foram acessados no dia 15/09/2023 e não há garantia de que continuem funcionando no futuro. Contate a fonte da informação para dúvidas.
Os pré-processamentos de dados realizados para a finalidade de classificação via regressão logística são:
- Países sem informação de PIB para 2019 são tratados como valor ausente e deixados de fora da análise;
- É utilizada a amostragem aleatória estratificada para separar duas amostras: 70% para treino e o restante para teste.
- Valores extremos do PIB, detectados pela regra de corte IQR sugerida por Hyndman e Athanasopoulos (2021), são removidos das amostras;
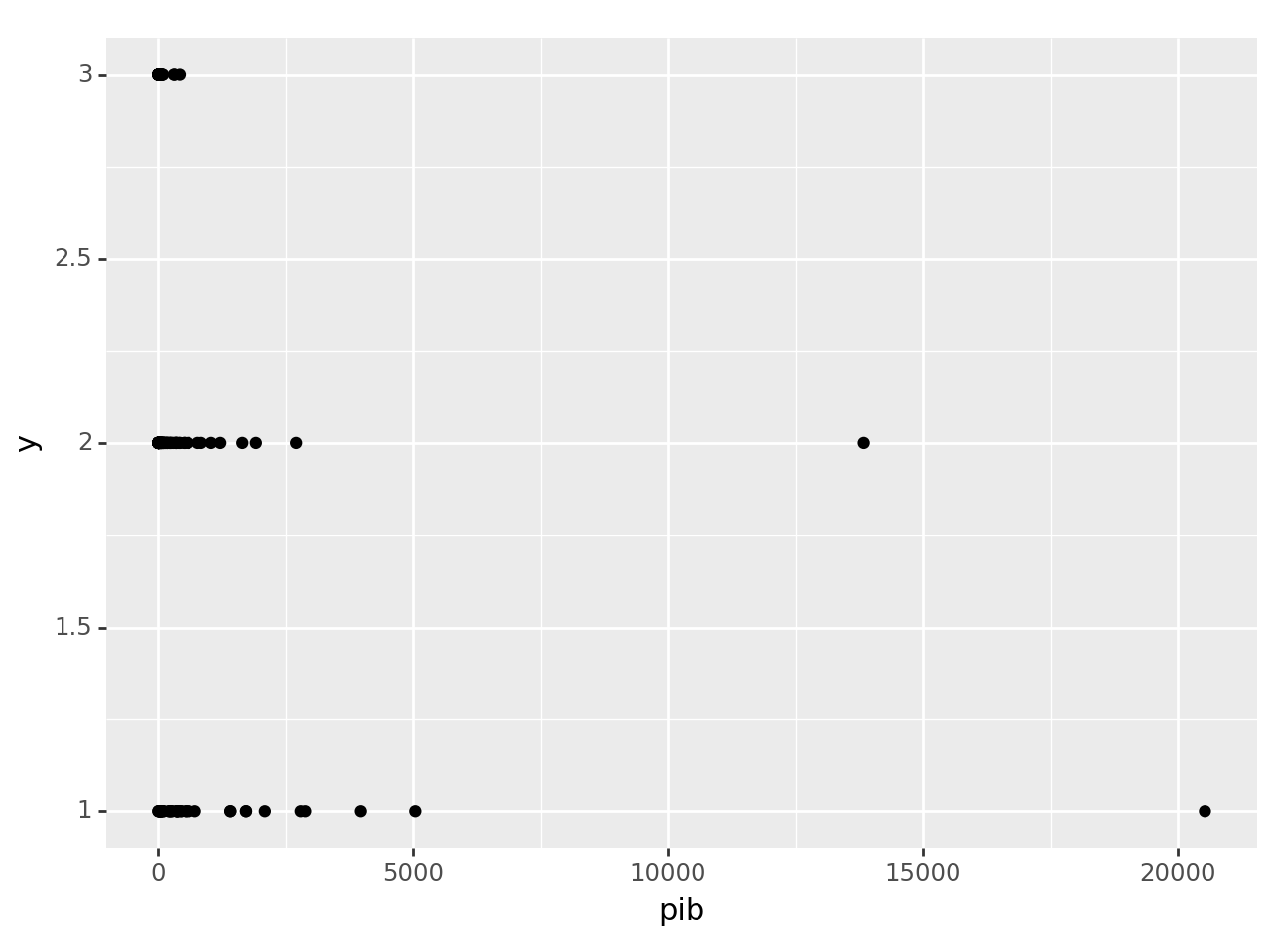
Uma visualização de dados, antes da separação das amostras e remoção de valores extremos, é exibida abaixo:
# Importa bibliotecas
import pandas as pd
import numpy as np
import dbnomics
import plotnine as p9
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix, accuracy_score
# Carrega dados
dados_brutos_y = pd.read_excel(
io = "https://www.imf.org/external/datamapper/Metadata_Apr2023.xlsx",
sheet_name = "Table A. Economy Groupings",
usecols = "A:C",
nrows = 95
)
dados_brutos_x = dbnomics.fetch_series_by_api_link(
api_link = "https://api.db.nomics.world/v22/series/IMF/WEO:2023-04?" +
"dimensions=%7B%22unit%22%3A%5B%22us_dollars%22%5D%2C%22" +
"weo-subject%22%3A%5B%22NGDPD%22%5D%7D&observations=1",
max_nb_series = 99999
)
# Pré-processamentos
dados_y = (
dados_brutos_y
.rename(
columns = {
"Advanced Economies": "avancada",
"Emerging\nMarket Economies\n": "emergentes",
"Low-Income Developing\nCountries\n": "baixa_renda"
}
)
.melt(var_name = "y", value_name = "pais")
.dropna()
.assign(
y = lambda x: np.where(x.y == "avancada", 1, np.where(x.y == "emergentes", 2, 3))
)
.set_index("pais")
)
dados_x = (
dados_brutos_x
.groupby("weo-country", as_index = False)
.apply(lambda x: x.query("not value.isna()"))
.groupby("weo-country", as_index = False)
.apply(lambda x: x.query("original_period == '2018'"))
.filter(items = ["WEO Country", "value"])
.rename(columns = {"WEO Country": "pais", "value": "pib"})
.reset_index(drop = True)
.set_index("pais")
)
dados = (
dados_y
.join(other = dados_x, on = "pais", how = "left")
.dropna()
.reset_index()
)
# Visualização de dados
print(
p9.ggplot(dados) +
p9.aes(x = "pib", y = "y") +
p9.geom_point()
)
As classificações do algoritmo k-vizinhos mais próximos são exibidas abaixo:
# Separação de amostras
dados_treino, dados_teste = train_test_split(
dados,
test_size = 0.3,
random_state = 1984,
stratify = dados.y
)
# Função para computar regra de corte IQR
def regra_iqr(x, side):
quantiles = x.quantile([0.25, 0.75])
iqr = quantiles[0.75] - quantiles[0.25]
if side == "lower":
return quantiles[0.25] - 1.5 * iqr
elif side == "upper":
return quantiles[0.75] + 1.5 * iqr
else:
raise Exception("side tem que ser lower ou upper")
y_lower_treino = regra_iqr(dados_treino.pib, 'lower')
y_upper_treino = regra_iqr(dados_treino.pib, 'upper')
y_lower_teste = regra_iqr(dados_teste.pib, 'lower')
y_upper_teste = regra_iqr(dados_teste.pib, 'upper')
# Filtra dados
dados_treino = dados_treino.query("pib > @y_lower_treino and pib < @y_upper_treino")
dados_teste = dados_teste.query("pib > @y_lower_teste and pib < @y_upper_teste")
# Classificação por k-vizinhos próximos
algoritmo = KNeighborsClassifier(
n_neighbors = int(np.sqrt(dados_treino.shape[0]))
)
algoritmo.fit(
X = dados_treino.filter(["pib"]),
y = dados_treino.y.values.ravel()
)
classificacao_teste = algoritmo.predict(dados_teste.filter(["pib"]))
classificacao_teste
array([2, 2, 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 2,
2, 3, 3, 2, 2, 2, 2, 2])Por fim reportamos medidas de acurácia explicadas aqui:
# Medidas de acurácia confusion_matrix(dados_teste.y, classificacao_teste) accuracy_score(dados_teste.y, classificacao_teste)
0.5192307692307693
Conclusão
Me mostre seus amigos e te direi quem és? Nesse artigo apresentamos a intuição e o funcionamento do algoritmo k-vizinhos próximos (k-NN) para problemas de classificação. Damos um exemplo com dados de classificação de economias em avançadas, emergentes ou baixa renda e usamos as linguagens R e Python.
Quer aprender mais?
- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;
- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;
- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.
Referências
Brett Lantz. Machine Learning with R. Packt Publishing, 2013.