Entender as características gerais dos dados é uma das primeiras etapas de um projeto de ciência ou análise de dados. É como se sentar no banco do motorista de um carro que você nunca dirigiu na vida: primeiro você vai querer se ambientar e entender os principais comandos de direção do veículo e, então, ter mais confiança para pilotar o veículo.
De forma análoga, um cientista ou analista de dados precisa primeiro entender os dados para, então, desenvolver uma análise preditiva, diagnóstica ou prescritiva. Em certa medida, podemos dizer que a base de tudo isso é uma boa análise descritiva.
Sendo assim, neste artigo vamos navegar pelas definições, fórmulas, cálculos e computação das estatísticas descritivas, como forma de entendimento de dados do tipo série temporal e/ou corte transversal. Além disso, mostraremos na prática, em R e Python, como gerar um sumário para reportar e analisar os dados rapidamente.
O que são estatísticas descritivas de dados?
As estatísticas descritivas desempenham um papel fundamental na análise de dados, fornecendo insights valiosos sobre as características e padrões de um conjunto de dados. Antes de mergulhar em técnicas analíticas avançadas, é essencial ter um bom domínio das estatísticas descritivas. A seguir, vamos explorar o que são estatísticas descritivas e discutir sua relevância na análise tanto de dados de séries temporais quanto de dados de corte transversal.
Estatísticas descritivas envolvem resumir e apresentar dados de forma significativa para descobrir características-chave, tendências e distribuições. Elas nos permitem obter uma compreensão inicial do conjunto de dados, identificar valores atípicos, medir tendências centrais e avaliar a variabilidade ou dispersão das variáveis. Ao utilizar várias medidas estatísticas, podemos obter insights significativos e tomar decisões informadas com base nos dados observados.
Dados de séries temporais
Ao lidar com dados de séries temporais, que são coletados ao longo de uma sequência de períodos de tempo, certas estatísticas descritivas se tornam particularmente relevantes. Essas estatísticas nos ajudam a entender o comportamento temporal e os padrões exibidos pelos dados. Algumas estatísticas descritivas importantes para a análise de séries temporais incluem:
- Medidas de tendência central: isso inclui a média, mediana e moda, que fornecem insights sobre o valor médio ou típico da série temporal.
- Medidas de dispersão: desvio padrão, variância e amplitude são úteis para avaliar a variabilidade ou dispersão dos pontos de dados ao longo da série temporal.
- Análise de tendência: estatísticas obtidas pela regressão linear e médias móveis ajudam a identificar tendências, sejam elas crescentes, decrescentes ou estacionárias, ao longo do tempo.
- Sazonalidade e periodicidade: ao examinar estatísticas descritivas como autocorrelação e análise espectral, podemos detectar padrões sazonais ou flutuações periódicas dentro da série temporal.
Dados de corte transversal
Por outro lado, ao trabalhar com dados de corte transversal, que representam observações realizadas em um ponto específico no tempo, diferentes estatísticas descritivas são relevantes. Essas estatísticas oferecem insights sobre a distribuição e as relações entre as variáveis em um determinado momento. Aqui estão algumas estatísticas descritivas importantes para a análise de dados de corte transversal:
- Distribuição de frequência: fornece um resumo da frequência com que diferentes valores ocorrem para uma variável específica, usualmente representada por meio de histogramas ou gráficos de barras.
- Medidas de associação: estatísticas descritivas como coeficientes de correlação (por exemplo, correlação de Pearson) e tabelas de contingência ajudam a entender as relações e dependências entre as variáveis.
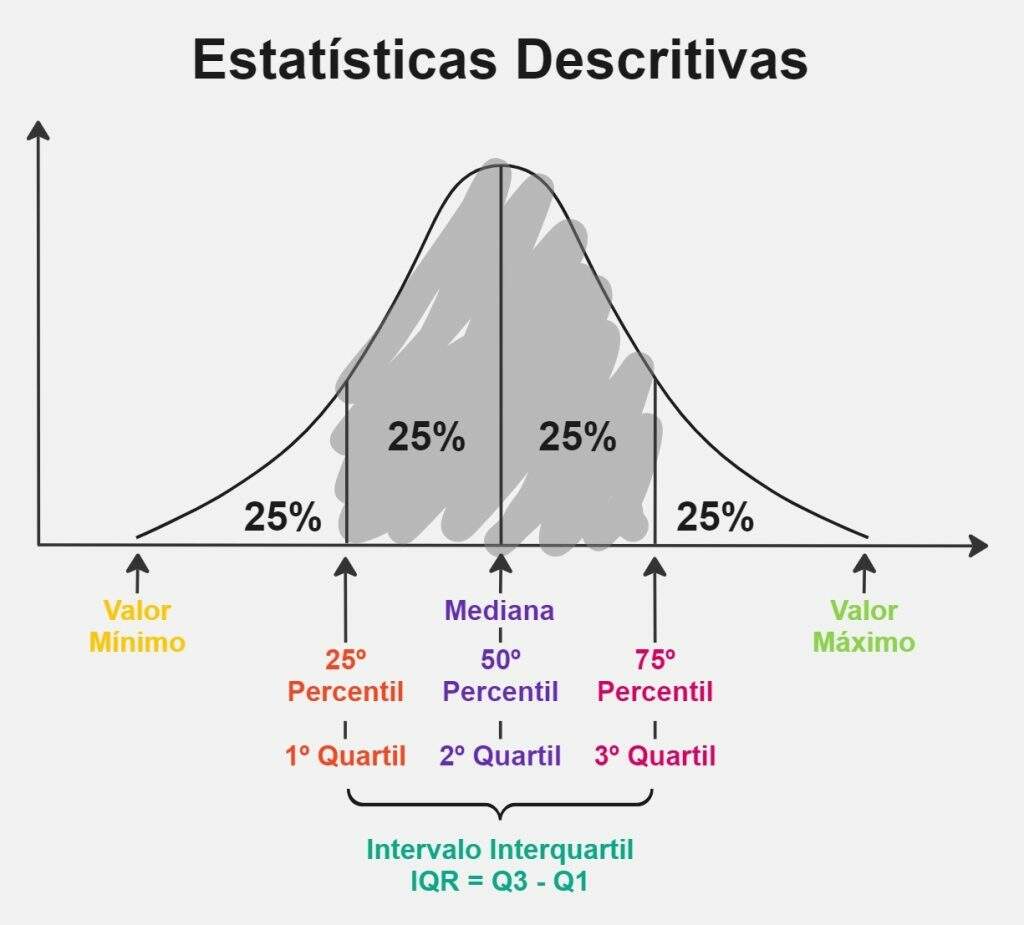
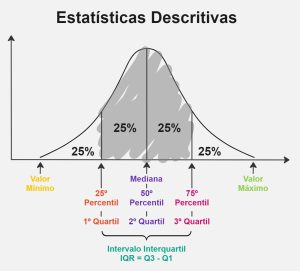
- Sumário de estatísticas: inclui valores mínimos e máximos, quartis e percentis, que fornecem uma visão abrangente do intervalo e distribuição do conjunto de dados.
- Análise de dados categóricos: estatísticas descritivas como moda e proporções são úteis para analisar variáveis categóricas e entender a prevalência ou distribuição de diferentes categorias.
Ao aproveitar essas estatísticas descritivas, analistas e pesquisadores podem obter insights valiosos sobre os padrões e características subjacentes tanto de dados de séries temporais quanto de dados de corte transversal. Esses insights servem como base para análises e processos de tomada de decisão mais aprofundados, levando a conclusões e ações mais informadas.
Fórmulas e cálculos de estatísticas descritivas
As estatísticas descritivas fornecem ferramentas essenciais para analisar e resumir dados. Sendo assim, vamos entender de maneira um pouco mais formal as diversas estatísticas descritivas importantes, incluindo a média, mediana, mínimo, máximo, percentis, frequência, desvio padrão e variância. Compreender como calcular essas estatísticas é crucial para obter insights dos seus dados. Vamos detalhar cada uma delas:
Média
A média representa o valor médio de um conjunto de dados e é calculada somando todos os valores e dividindo pelo número total de observações.
Fórmula: , onde Xi representa cada observação no conjunto de dados e n é o número total de observações.
Mediana
A mediana representa o valor central de um conjunto de dados quando ordenado em ordem crescente ou decrescente. É útil para identificar a tendência central e é menos sensível a valores atípicos.
Fórmula: ordene o conjunto de dados em ordem crescente ou decrescente e, em seguida, selecione o valor do meio.
Mínimo
O mínimo é o menor valor em um conjunto de dados e fornece insights sobre o limite inferior dos dados.
Fórmula: Xmin = min(X1, X2, ..., Xn), onde Xi representa cada observação no conjunto de dados.
Máximo
O máximo é o maior valor em um conjunto de dados e indica o limite superior dos dados.
Fórmula: Xmax = max(X1, X2, ..., Xn), onde Xi representa cada observação no conjunto de dados.
Percentis
Os percentis dividem um conjunto de dados em partes iguais, indicando os valores abaixo dos quais uma certa porcentagem dos dados se encontra. Os percentis comuns incluem o 25º percentil (primeiro quartil), 50º percentil (mediana ou segundo quartil) e 75º percentil (terceiro quartil).
Fórmula: há pelo menos 9 algoritmos diferentes para computar percentis, veja detalhes nesse link.
Frequência
Frequência refere-se ao número de vezes que um determinado valor ocorre em um conjunto de dados. Ajuda a entender a distribuição e prevalência de valores específicos.
Fórmula: contar as ocorrências de cada valor único no conjunto de dados.
Desvio Padrão
O desvio padrão mede a dispersão ou variabilidade de um conjunto de dados. Quantifica o quanto os valores se desviam da média.
Fórmula: 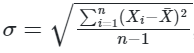
Variância
A variância é o valor ao quadrado do desvio padrão e fornece uma medida do desvio médio ao quadrado em relação à média.
Fórmula: , onde Xi representa cada observação no conjunto de dados e Xbarra é a média.
Lembre-se de que estar familiarizado com esses cálculos capacita você a extrair informações significativas dos seus dados e chegar a conclusões precisas.
Como gerar um sumário de estatísticas descritivas?
Ter uma visão geral sobre os cálculos de estatísticas descritivas pode ajudar a não cometer análises errôneas. Na prática, porém, não é necessário decorar as fórmulas e algoritmos, pois as principais ferramentas e linguagens de programação existentes atualmente já trazem estes procedimentos prontos para aplicação. De toda forma, ferramentas são apenas ferramentas e só ganham utilidade se o usuário tiver um conhecimento de base estatística sólido para aplicação e uso adequado.
A seguir mostramos a aplicação, usando linguagem de programação, de cálculos de estatísticas descritivas que são facilmente reportadas em um sumário, facilitando a análise e apresentação das características principais dos dados:
R
Código
| Variable | Mean | SD | IQR | Min | Max | Skewness | Kurtosis | n | n_Missing |
|---|---|---|---|---|---|---|---|---|---|
| ano_campeonato | 2.020000e+03 | 0.000000e+00 | 0.0000e+00 | 2.02e+03 | 2020.0 | NaN | NaN | 380 | 0 |
| rodada | 1.950000e+01 | 1.098031e+01 | 1.9000e+01 | 1.00e+00 | 38.0 | 0.0000000 | -1.2016685 | 380 | 0 |
| publico | 0.000000e+00 | 0.000000e+00 | 0.0000e+00 | 0.00e+00 | 0.0 | NaN | NaN | 380 | 0 |
| publico_max | 4.534465e+04 | 1.982209e+04 | 3.0326e+04 | 1.25e+04 | 82238.0 | -0.1111147 | -0.8364307 | 380 | 0 |
| colocacao_man | 1.057368e+01 | 5.723381e+00 | 9.0000e+00 | 1.00e+00 | 20.0 | 0.0031620 | -1.1874276 | 380 | 0 |
| colocacao_vis | 1.042632e+01 | 5.823013e+00 | 1.1000e+01 | 1.00e+00 | 20.0 | -0.0017077 | -1.2255431 | 380 | 0 |
| valor_equipe_titular_man | 2.108354e+07 | 1.584535e+07 | 2.0350e+07 | 3.85e+06 | 81250000.0 | 1.5110308 | 2.4024934 | 367 | 13 |
| valor_equipe_titular_vis | 2.068114e+07 | 1.582978e+07 | 2.0450e+07 | 2.93e+06 | 79050000.0 | 1.4393257 | 1.8546916 | 367 | 13 |
| idade_media_titular_man | 2.746703e+01 | 1.529984e+00 | 2.3000e+00 | 2.16e+01 | 31.2 | -0.2433071 | 0.3053785 | 367 | 13 |
| idade_media_titular_vis | 2.729455e+01 | 1.643042e+00 | 2.2000e+00 | 2.15e+01 | 31.9 | -0.2522215 | 0.4524520 | 367 | 13 |
| gols_man | 1.410526e+00 | 1.101639e+00 | 1.0000e+00 | 0.00e+00 | 5.0 | 0.5262164 | -0.3001129 | 380 | 0 |
| gols_vis | 1.073684e+00 | 1.060115e+00 | 2.0000e+00 | 0.00e+00 | 5.0 | 1.2149052 | 1.7923872 | 380 | 0 |
| gols_1_tempo_man | 6.736842e-01 | 8.016093e-01 | 1.0000e+00 | 0.00e+00 | 4.0 | 1.2441869 | 1.6209899 | 380 | 0 |
| gols_1_tempo_vis | 4.605263e-01 | 6.257616e-01 | 1.0000e+00 | 0.00e+00 | 3.0 | 1.0916745 | 0.4251177 | 380 | 0 |
| escanteios_man | 5.435829e+00 | 3.035076e+00 | 4.0000e+00 | 0.00e+00 | 17.0 | 0.6699906 | 0.3778435 | 374 | 6 |
| escanteios_vis | 4.705882e+00 | 2.717063e+00 | 3.0000e+00 | 0.00e+00 | 16.0 | 0.8289910 | 0.9046828 | 374 | 6 |
| faltas_man | 1.563636e+01 | 4.554274e+00 | 6.0000e+00 | 0.00e+00 | 29.0 | 0.1503128 | 0.3701115 | 374 | 6 |
| faltas_vis | 1.529947e+01 | 4.460268e+00 | 6.0000e+00 | 0.00e+00 | 31.0 | 0.1133481 | 0.3196081 | 374 | 6 |
| chutes_bola_parada_man | 1.454813e+01 | 4.389432e+00 | 5.2500e+00 | 0.00e+00 | 30.0 | 0.1488314 | 0.3084970 | 374 | 6 |
| chutes_bola_parada_vis | 1.467112e+01 | 4.547795e+00 | 5.0000e+00 | 0.00e+00 | 29.0 | 0.2390412 | 0.4409208 | 374 | 6 |
| defesas_man | 2.577540e+00 | 1.719819e+00 | 3.0000e+00 | 0.00e+00 | 8.0 | 0.6212421 | 0.1415856 | 374 | 6 |
| defesas_vis | 3.304813e+00 | 2.185285e+00 | 3.0000e+00 | 0.00e+00 | 10.0 | 0.7186879 | 0.4157609 | 374 | 6 |
| impedimentos_man | 1.483957e+00 | 1.357536e+00 | 2.0000e+00 | 0.00e+00 | 8.0 | 1.0973940 | 1.3946624 | 374 | 6 |
| impedimentos_vis | 1.473262e+00 | 1.294692e+00 | 1.0000e+00 | 0.00e+00 | 8.0 | 1.2217024 | 2.4133743 | 374 | 6 |
| chutes_man | 1.360428e+01 | 5.267492e+00 | 7.0000e+00 | 1.00e+00 | 31.0 | 0.6273910 | 0.2712918 | 374 | 6 |
| chutes_vis | 1.147861e+01 | 4.414614e+00 | 6.0000e+00 | 1.00e+00 | 31.0 | 0.4889927 | 0.6176898 | 374 | 6 |
| chutes_fora_man | 5.721925e+00 | 2.752079e+00 | 4.0000e+00 | 0.00e+00 | 15.0 | 0.5088137 | 0.1172051 | 374 | 6 |
| chutes_fora_vis | 4.925134e+00 | 2.536545e+00 | 3.0000e+00 | 0.00e+00 | 13.0 | 0.7503288 | 0.7703133 | 374 | 6 |
Python
Código
Downloading: 0%| | 0/380 [00:00<?, ?rows/s]
Downloading: 100%|##########| 380/380 [00:00<00:00, 932.65rows/s]
Downloading: 100%|##########| 380/380 [00:00<00:00, 930.37rows/s]Código
count unique ... 75% max
ano_campeonato 380.0 <NA> ... 2020.0 2020.0
data 380 132 ... NaN NaN
horario 380 22 ... NaN NaN
rodada 380.0 <NA> ... 29.0 38.0
estadio 380 22 ... NaN NaN
arbitro 380 39 ... NaN NaN
publico 380.0 <NA> ... 0.0 0.0
publico_max 380.0 <NA> ... 60326.0 82238.0
time_man 380 20 ... NaN NaN
time_vis 380 20 ... NaN NaN
tecnico_man 367 49 ... NaN NaN
tecnico_vis 367 52 ... NaN NaN
colocacao_man 380.0 <NA> ... 15.0 20.0
colocacao_vis 380.0 <NA> ... 16.0 20.0
valor_equipe_titular_man 367.0 <NA> ... 28400000.0 81250000.0
valor_equipe_titular_vis 367.0 <NA> ... 28200000.0 79050000.0
idade_media_titular_man 367.0 NaN ... 28.55 31.2
idade_media_titular_vis 367.0 NaN ... 28.4 31.9
gols_man 380.0 <NA> ... 2.0 5.0
gols_vis 380.0 <NA> ... 2.0 5.0
gols_1_tempo_man 380.0 <NA> ... 1.0 4.0
gols_1_tempo_vis 380.0 <NA> ... 1.0 3.0
escanteios_man 374.0 <NA> ... 7.0 17.0
escanteios_vis 374.0 <NA> ... 6.0 16.0
faltas_man 374.0 <NA> ... 18.0 29.0
faltas_vis 374.0 <NA> ... 18.0 31.0
chutes_bola_parada_man 374.0 <NA> ... 17.0 30.0
chutes_bola_parada_vis 374.0 <NA> ... 17.0 29.0
defesas_man 374.0 <NA> ... 4.0 8.0
defesas_vis 374.0 <NA> ... 5.0 10.0
impedimentos_man 374.0 <NA> ... 2.0 8.0
impedimentos_vis 374.0 <NA> ... 2.0 8.0
chutes_man 374.0 <NA> ... 17.0 31.0
chutes_vis 374.0 <NA> ... 14.0 31.0
chutes_fora_man 374.0 <NA> ... 8.0 15.0
chutes_fora_vis 374.0 <NA> ... 6.0 13.0
[36 rows x 11 columns]Conclusão
Neste artigo entendemos sobre as principais estatísticas descritivas que analistas e cientistas de dados podem utilizar pra compreensão dos dados, permitindo análises e decisões mais informadas. Mostramos um pouco da base teórica de maneira didática e expomos a aplicação com um exemplo de conjunto de dados real.
Saiba mais
Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:
E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.
Referências
Wikipedia contributors. (2023, March 12). Descriptive statistics. In Wikipedia, The Free Encyclopedia. Retrieved 16:04, May 18, 2023, from https://en.wikipedia.org/w/index.php?title=Descriptive_statistics&oldid=1144142381