Desde a metade do primeiro semestre de 2023 a temperatura das águas do Oceano Pacífico equatorial se elevaram, atingindo um ponto de anomalia em agosto (NOOA). Este fenômeno é conhecido como “El Niño” e tem impactos generalizados em diversas áreas do globo, podendo afetar a precipitação e temperatura, que são fatores chave para o plantio e colheita de diversas culturas.
Para mensurar os efeitos do El Niño sobre os preços da alimentação dos brasileiros, neste artigo estimamos um modelo de vetores autoregressivos de ordem p ou, simplesmente, VAR(p), baseado em BCB (2019):
Para mensurar os efeitos do El Niño sobre os preços da alimentação dos brasileiros, neste artigo estimamos um modelo de vetores autoregressivos de ordem p ou, simplesmente, VAR(p), baseado em BCB (2019):
![\[y_t = \sum_{i=1}^p A_p y_{t-p} + z_t + \varepsilon_t\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-1fb1f06caaeb567753350b08b6e31fdb_l3.png "Rendered by QuickLaTeX.com")
onde:
- 
- 
é a taxa de inflação medida pelo IPCA, subgrupo alimentação no domicílio
- 
é o hiato do produto medido pela função de produção
- 
é a inflação externa, medida pelo Índice de Commodities - Brasil agropecuário
- 
é o Oceanic Niño Index (ONI), transformado como 
- 
inclui uma constante e dummies sazonais
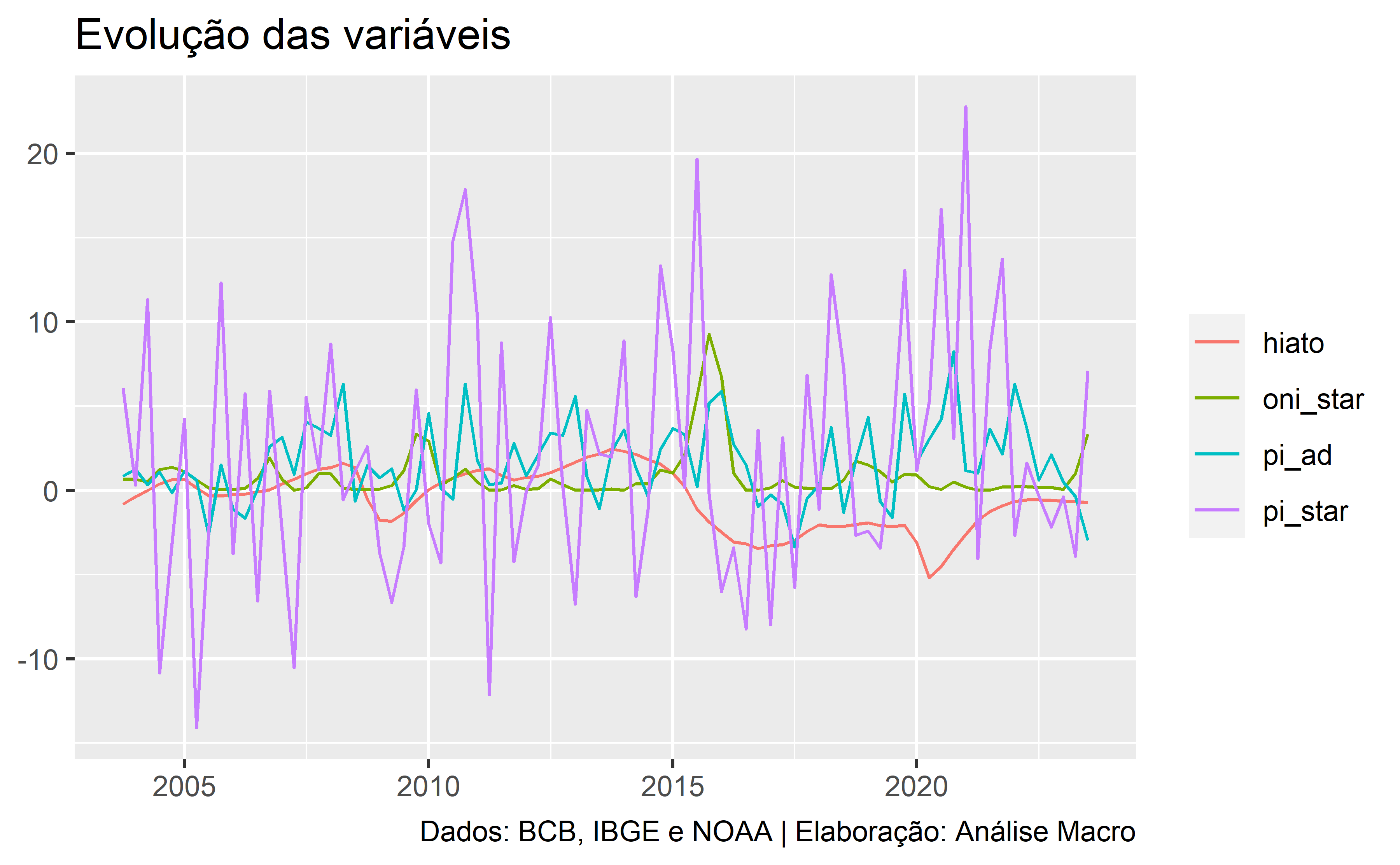
Utilizamos uma amostra de dados do quarto trimestre de 2003 ao terceiro trimestre de 2023. Outras informações e detalhes podem ser encontradas em BCB (2019). Os dados em frequência trimestral são expostos no gráfico abaixo:
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
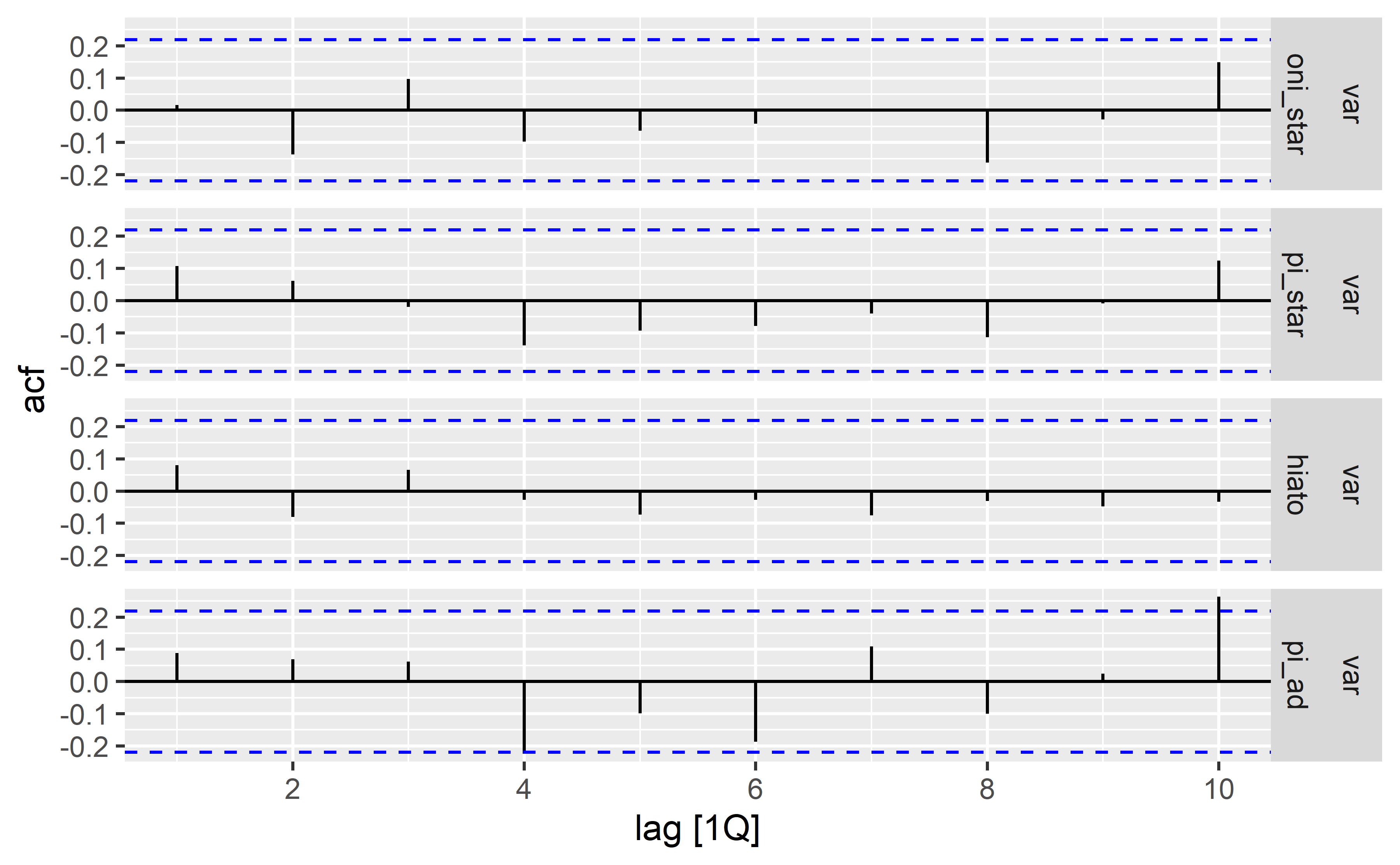
Abaixo exibimos os resultados estatísticos do modelo VAR:
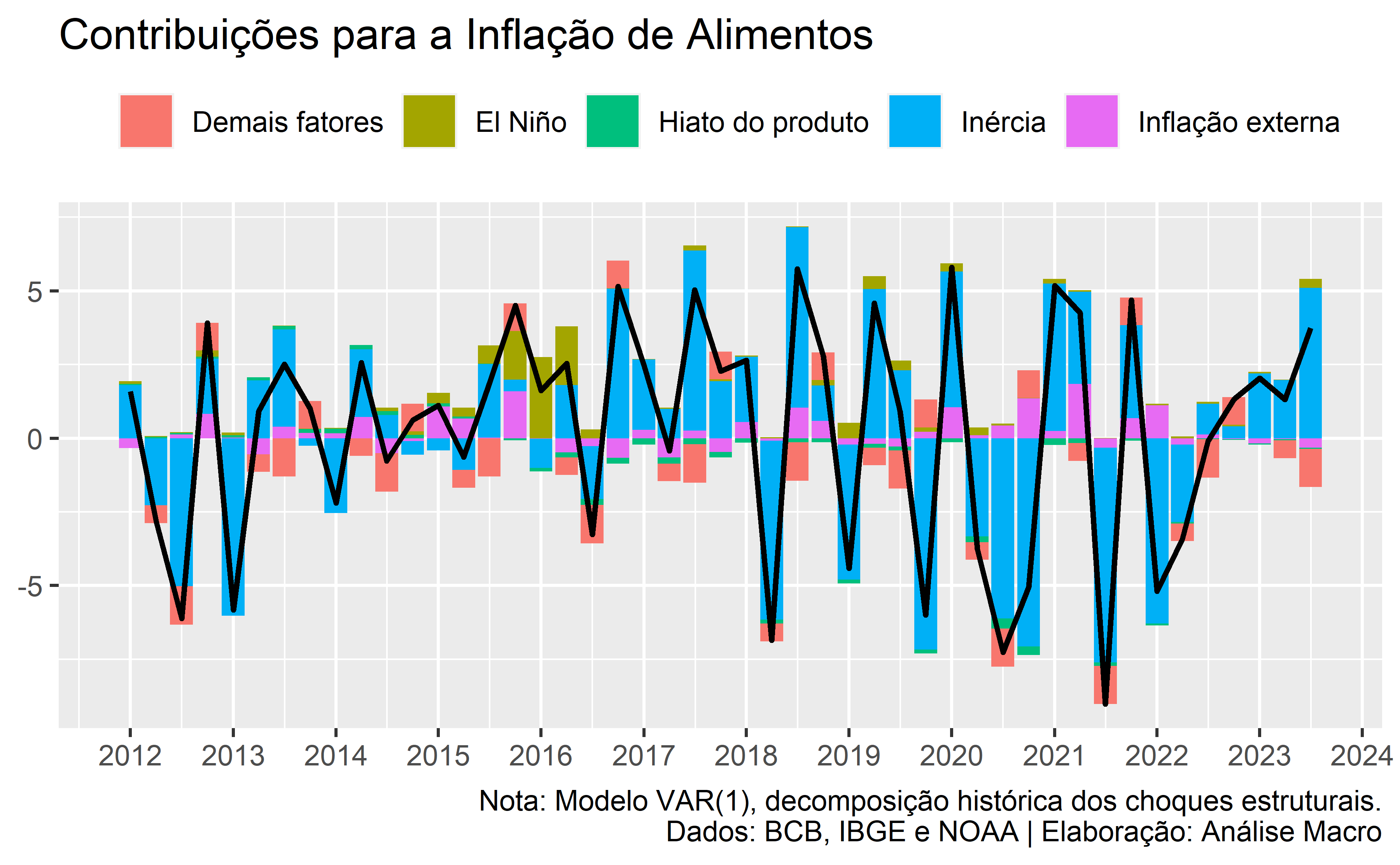
Series: oni_star, pi_star, hiato, pi_ad Model: VAR(3) w/ mean Coefficients for oni_star: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) 1.3077 0.0189 -0.1454 -0.0633 s.e. 0.1280 0.0141 0.2437 0.0522 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) -0.8657 0.0056 -0.0028 0.0216 s.e. 0.1845 0.0151 0.4201 0.0521 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant 0.2629 0.0008 0.1916 -0.0211 -0.1488 s.e. 0.1343 0.0148 0.2420 0.0497 0.2575 season().year2 season().year3 season().year4 0.3957 0.9270 0.6599 s.e. 0.3224 0.3201 0.3136 Coefficients for pi_star: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) 0.3929 -0.1429 -1.8525 0.7254 s.e. 1.1553 0.1269 2.1994 0.4710 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) -2.2887 0.1106 4.1782 -0.2966 s.e. 1.6649 0.1362 3.7911 0.4699 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant 1.1749 0.1617 -2.8212 -0.1620 0.5076 s.e. 1.2122 0.1340 2.1837 0.4481 2.3239 season().year2 season().year3 season().year4 -2.7310 1.7834 4.7214 s.e. 2.9092 2.8882 2.8295 Coefficients for hiato: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) -0.1230 0.0065 1.7018 0.0027 s.e. 0.0627 0.0069 0.1193 0.0255 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) 0.1914 -0.0104 -1.0377 -0.0286 s.e. 0.0903 0.0074 0.2056 0.0255 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant -0.1709 -0.0038 0.2652 0.0531 -0.0397 s.e. 0.0658 0.0073 0.1184 0.0243 0.1261 season().year2 season().year3 season().year4 -0.0053 0.1549 0.0457 s.e. 0.1578 0.1567 0.1535 Coefficients for pi_ad: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) 0.0428 0.1015 0.6524 0.0423 s.e. 0.3108 0.0341 0.5917 0.1267 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) 0.3378 0.0510 -1.3854 -0.0541 s.e. 0.4479 0.0367 1.0199 0.1264 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant -0.1455 0.0303 0.8795 0.3049 1.1845 s.e. 0.3261 0.0360 0.5875 0.1206 0.6252 season().year2 season().year3 season().year4 -0.5070 -1.7955 0.3972 s.e. 0.7827 0.7770 0.7612 Residual covariance matrix: oni_star pi_star hiato pi_ad oni_star 0.6806 1.1047 -0.0131 -0.0714 pi_star 1.1047 55.4166 0.0012 3.8450 hiato -0.0131 0.0012 0.1630 0.0947 pi_ad -0.0714 3.8450 0.0947 4.0110 log likelihood = -519.71 AIC = 1199.42 AICc = -2040.58 BIC = 1386.92O gráfico abaixo sintetiza as contribuições dos fatores para a variável de interesse, a inflação de alimentos, sob a ótica da decomposição histórica dos choques estruturais do modelo VAR. No período de 2015-2016, o fenômeno El Niño contribuiu consideravelmente para o aumento da inflação. No período da pandemia, de 2019 até 2021, a variável climática contribuiu para o aumento da inflação de forma menos expressiva. E mais recentemente, no terceiro trimestre de 2023, a variável climática começou a contribuir para o aumento da inflação novamente, porém em magnitude inferior em relação a períodos anteriores.
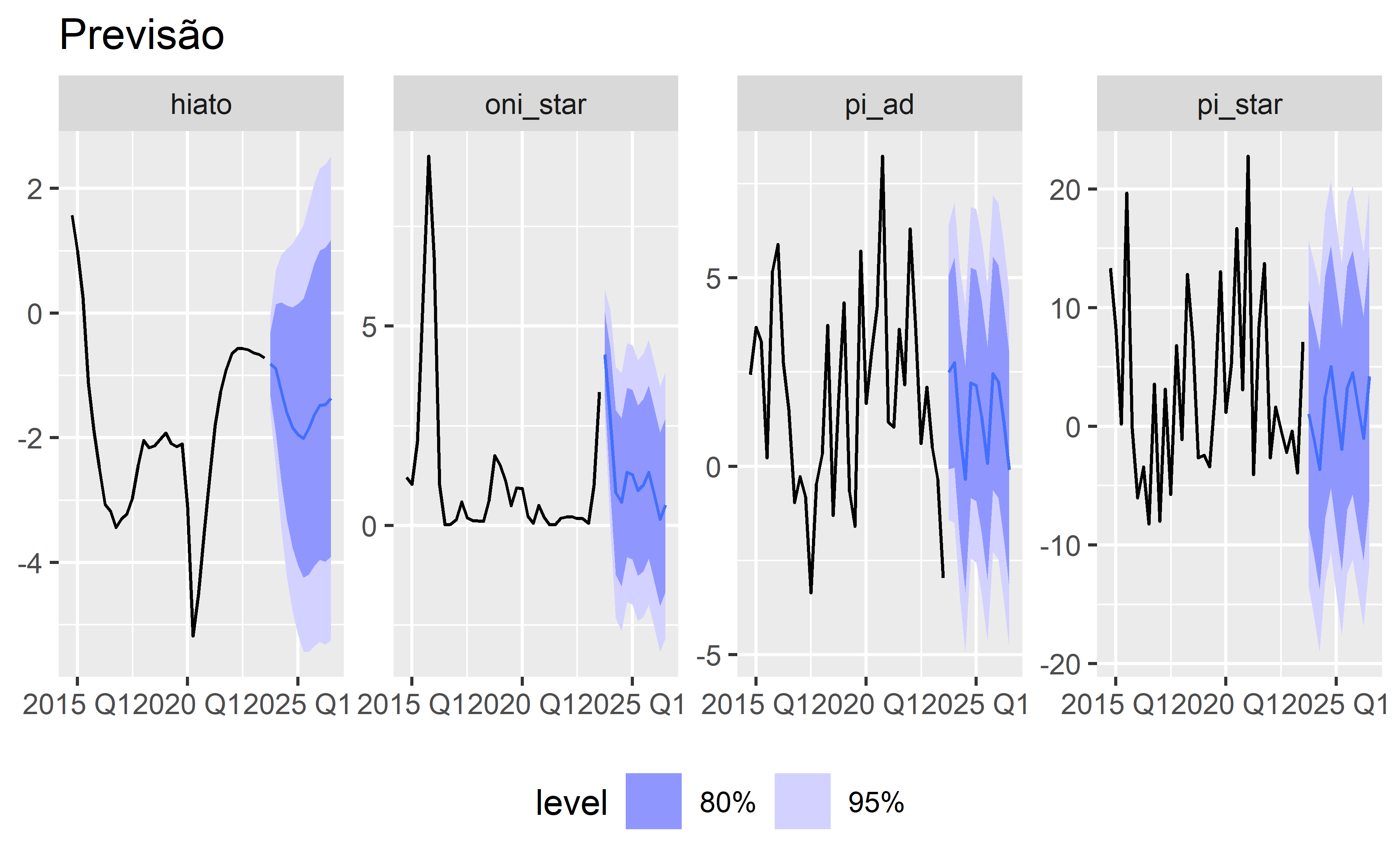
Uma vez identificado a importância da variável climática para a inflação de alimentos, incorporamos a mesma na previsão 12 períodos a frente. O gráfico abaixo apresenta as previsões para o período e variáveis do modelo:
Este artigo contribui marginalmente para a avaliação dos efeitos de impactos climáticos no desvio da trajetória de equilíbro da inflação de alimentos no Brasil no período atual.
Conclusão
Será que o El Niño impacta o preço do feijão com arroz no prato dos brasileiros? Para responder esta pergunta estimamos um modelo VAR(p) utilizando dados do Oceanic Niño Index (ONI), investigamos a decomposição histórica dos choques estruturais e incorporamos o indicador de impacto climático nas previsões da inflação.
Referências
BANCO CENTRAL DO BRASIL (2019). Impactos do clima na inflação de alimentos. Estudo Especial nº 57/2019.
Tenha acesso ao código e suporte desse e de mais 500 exercícios no Clube AM!
Quer o código desse e de mais de 500 exercícios de análise de dados com ideias validadas por nossos especialistas em problemas reais de análise de dados do seu dia a dia? Além de acesso a vídeos, materiais extras e todo o suporte necessário para você reproduzir esses exercícios? Então, fale com a gente no Whatsapp e veja como fazer parte do Clube AM, clicando aqui.
