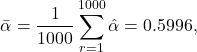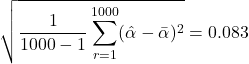Métodos de Reamostragem

Introdução

Métodos de reamostragem são ferramentas indispensáveis na estatística moderna. Eles envolvem, basicamente, extrair de forma repetida amostras de um conjunto de treino de modo a reestimar o modelo de interesse em cada uma das amostras, obtendo assim informação adicional sobre o modelo ajustado. Vamos conhecer dois métodos úteis aplicáveis a dados de séries temporais de forma a auxiliar previsões: cross-validation e bootstrap.

Nessa seção, vamos estudar dois métodos bastantes utilizados na literatura:

• cross validation: método largamente utilizado para estimar o *erro de teste* associado a um dado método de aprendizado de modo a avaliar sua performance ou selecionar o grau de flexibilidade;
• bootstrap: método utilizado em diferentes contextos, mas comumente para prover uma medida de acurácia para um parâmetro estimado.

Cross Validation é uma versão mais sofisticada da ideia que adotamos até aqui de dividir a nossa amostra em dois conjuntos estáticos de treino e de teste, de modo a computar o erro de teste, isto é, a diferença entre a variável prevista e a variável efetivamente observada.

A abordagem de conjunto de validação: Treino e Teste

Antes de fazer referência ao método de cross validation de forma específica, vamos apresentar a abordagem de conjunto de validação de forma geral, isto é, a abordagem de separar os dados em treino e teste.

Quando avaliamos um modelo de série temporal, a dimensão dos resíduos não é uma indicação confiável da dimensão provável dos erros de previsão verdadeiros.

A precisão das previsões só pode ser determinada considerando o desempenho de um modelo com novos dados que não foram utilizados no ajuste do modelo.

A prática comum é separar os dados disponíveis em duas partes, dados de treinamento e dados de teste (training and test), onde os dados de treinamento são usados para estimar quaisquer parâmetros de um método de previsão e os dados de teste são usados para avaliar sua precisão.

Como os dados de teste não são usados na determinação das previsões, eles devem fornecer uma indicação confiável de quão bem o modelo provavelmente fará previsões com base em novos dados.

O tamanho do conjunto de teste é normalmente cerca de 20% da amostra total, embora esse valor dependa do tamanho da amostra e do quão adiante você deseja prever. Idealmente, o conjunto de testes deve ser pelo menos tão grande quanto o horizonte máximo de previsão exigido. Os seguintes pontos devem ser observados.

• Um modelo que se ajusta bem aos dados de treinamento não fará necessariamente uma boa previsão.
• Um ajuste perfeito sempre pode ser obtido usando um modelo com parâmetros suficientes.
• Ajustar excessivamente um modelo aos dados é tão ruim quanto não conseguir identificar um padrão sistemático nos dados.

Outras referências chamam o conjunto de treinamento de “dados dentro da amostra” (in-sample) e o conjunto de teste de “dados fora da amostra” (out-of-sample).

Time Series Cross Validation

Uma versão mais sofisticada de conjuntos de treinamento/teste é a validação cruzada de séries temporais.

Neste procedimento, há uma série de conjuntos de testes, cada um consistindo em uma única observação. O conjunto de treinamento correspondente consiste apenas em observações que ocorreram antes da observação que forma o conjunto de teste.

Assim, nenhuma observação futura pode ser usada na construção da previsão. Como não é possível obter uma previsão confiável com base em um pequeno conjunto de treinamento, as primeiras observações não são consideradas conjuntos de teste.

O diagrama a seguir ilustra um esquema de validação cruzada de séries temporais, com uma série de amostras de treino e de teste, para quando se deseja avaliar a performance preditiva do modelo em h = 1 períodos à frente, onde as observações azuis formam as amostras de treino e as observações laranja formam as amostras de teste.

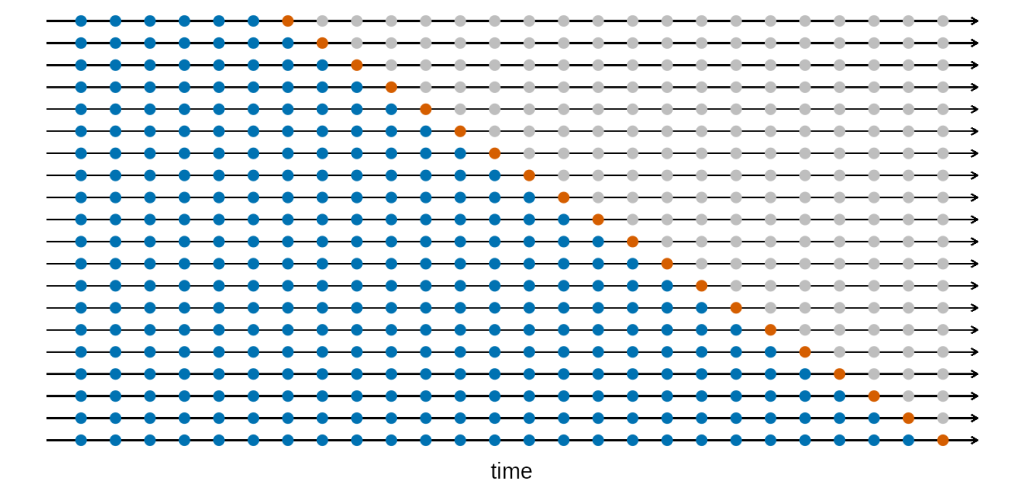
A precisão da previsão é calculada pela média dos conjuntos de teste. Este procedimento é por vezes conhecido como “avaliação na origem de previsão contínua (rolling forecast)” porque a “origem” na qual a previsão se baseia avança no tempo.

Com a previsão de séries temporais, as previsões em uma etapa podem não ser tão relevantes quanto as previsões em várias etapas. Neste caso, o procedimento de validação cruzada baseado em uma origem de previsão contínua pode ser modificado para permitir a utilização de erros em múltiplas etapas.

Suponha que estamos interessados em modelos que produzam boas previsões em 4 passos à frente. Podemos usar o diagrama abaixo para ilustrar.

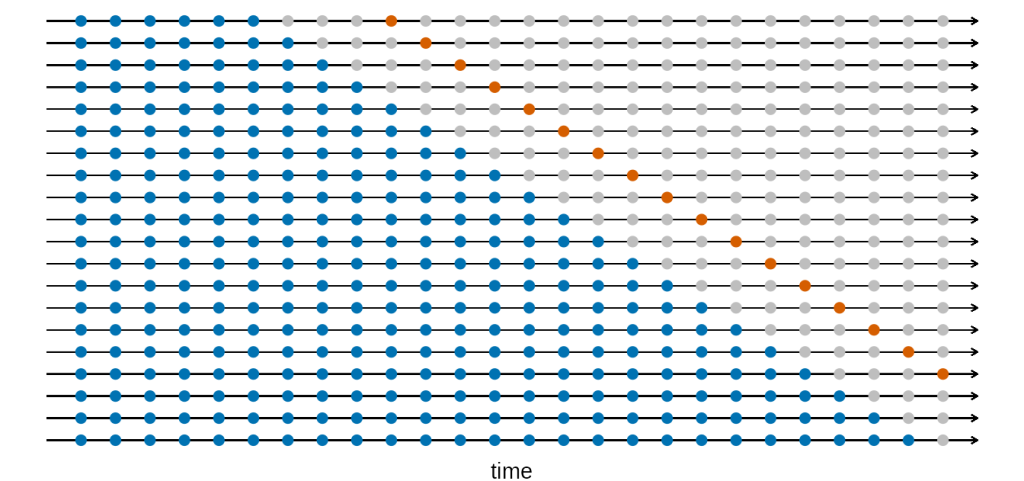
Operacionalização

Dado esse esquema de separação de uma série de amostras de treino e de teste de uma série temporal, o método de validação cruzada pode ser resumido como um procedimento recursivo:

1. Para cada amostra de treino estime o modelo;

2. Utilize o modelo estimado para gerar previsões h períodos à frente;

3. Calcule o erro de previsão com a amostra de teste e a saída da etapa 2.

Ao final, obtém-se a métrica de acurácia (ME, RMSE, MAE, etc.) do modelo pela média de cada iteração.

Bootstrap

Bootstrap é uma ferramenta estatística bastante útil para quantificar a incerteza associada a um dado estimador ou método de aprendizado estatístico.

Por exemplo, o método de bootstrap pode ser usado para estimar os erros padrão de um coeficiente em uma regressão linear.

Para ilustrar o método, vamos usar um exemplo fictício. Suponha que nós queremos investir uma soma fixa de dinheiro em dois ativos financeiros que possuem retornos de e .

Nós iremos investir uma fração do nosso dinheiro em e o restante em .

Dado que existe variabilidade associado aos retornos desses dois ativos, nós queremos escolher de modo a minimizar o risco total, ou variância, do nosso investimento. O valor de que minimiza o risco será dado então por

(1)  

onde , e .

Nós podemos obter estimativas para a partir de uma data set simulado.

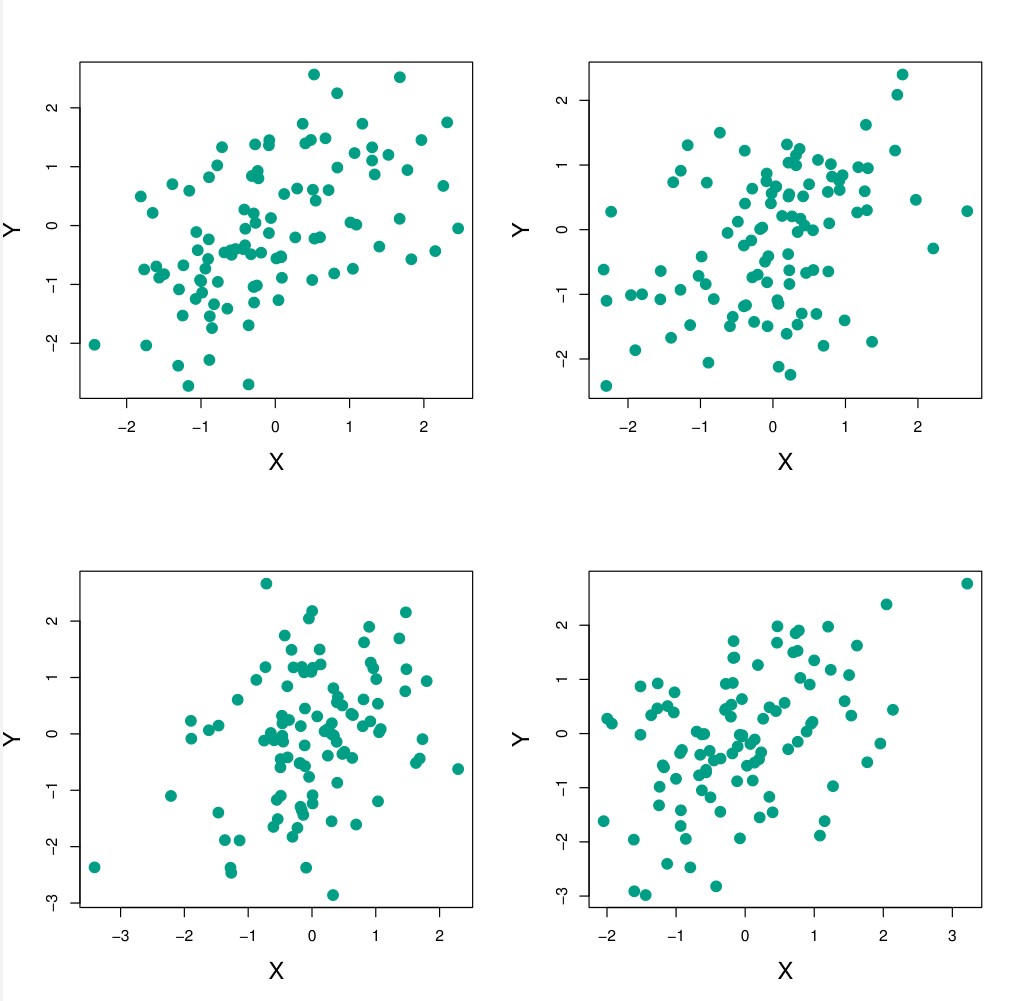
Utilizamos os retornos para então estimar , e . Uma vez obtidas essas métricas, podemos obter entre e .

Uma vez obtido , nós podemos nos perguntar sobre a *acurácia* dessa medida. Para isso, podemos estimar o desvio padrão de , ao repetir o processo de simular 100 pares de e e estimar 1000 vezes.

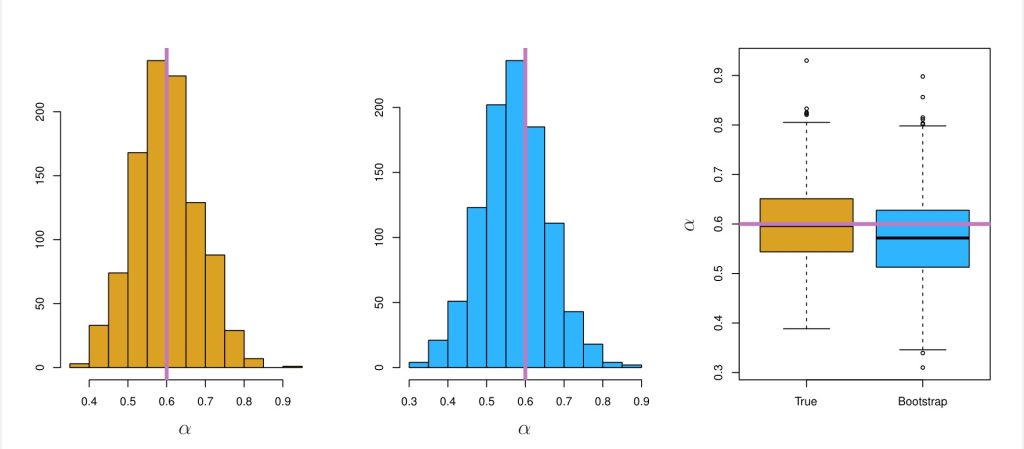
A estimativa média para será

(2)  

o que é muito próximo de e o desvio padrão será

(3)  

Para dados reais, contudo, o processo de estimar o desvio padrão não pode ser aplicado, dado que nós não podemos gerar novas amostras a partir da população original.

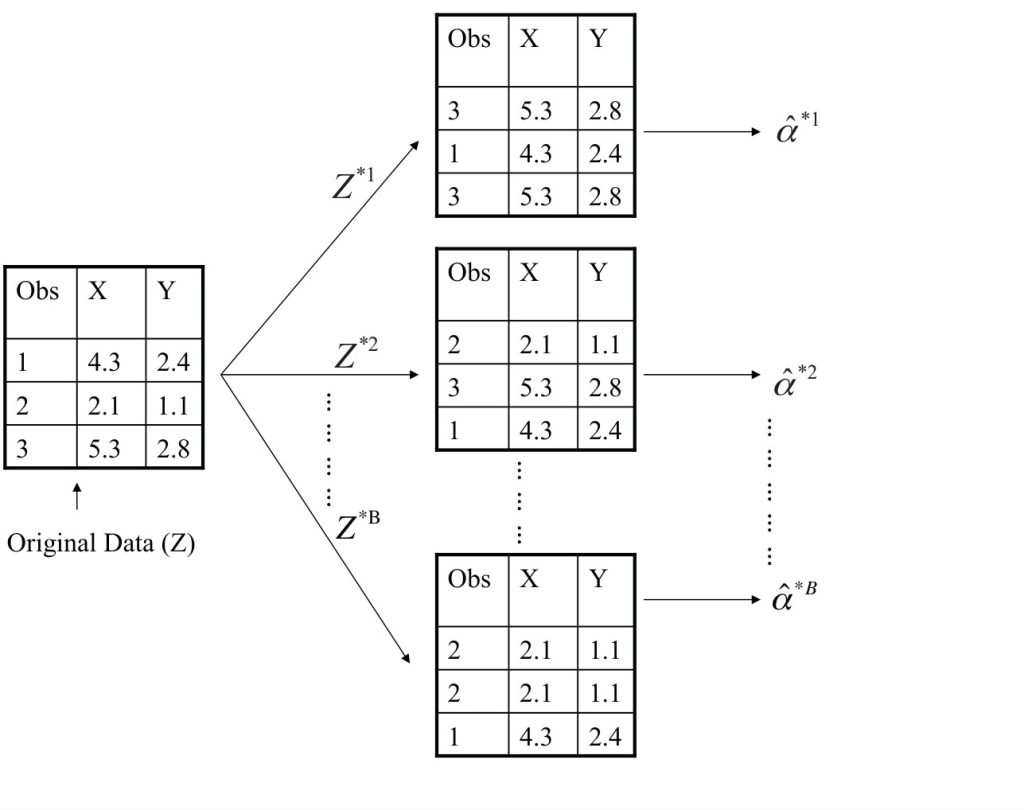
A abordagem de bootstrap*permite assim *emular* o processo de observar novas amostras, de modo a estimar a variabilidade de sem gerar amostras adicionais. Nós iremos obter distintos data sets ao repetidamente amostrar observações a partir do data set original.

Referências

James, Gareth; Witten, Daniela; Hastie, Trevor; Tibshirani, Robert. An Introduction to Statistical Learning with Applications in R. Second Edition. Springer

Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-09-04.

Quer aprender mais?

 -  Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;

 - Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;

 - Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.