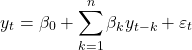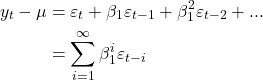O que são os modelos ARIMA e como aplicar a Metodologia Box-Jenkins? Vamos demonstrar neste post como construir um modelo linear univariado, expondo o modelo do tipo ARIMA, bem como vamos descrever a metodologia Box-Jenkins para prever séries temporais. Mostraremos os resultados de um exemplo da previsão do IPCA mensal construído no R e no Python.
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Introdução a modelos lineares univariados
Em termos simples, o objetivo da econometria de séries temporais univariada é encontrar a dependência dinâmica de uma série , isto é, a dependência de
em relação aos seus valores passados (
).
Aqui focaremos nos modelos univariados lineares, onde depende linearmente dos seus valores passados.
Como veremos, modelos univariados podem ser uma boa forma de gerar previsões simples e rápidas para séries que, a priori, nós não temos maiores informações sobre variáveis exógenas que podem influenciar o seu comportamento.
Ademais, com processos que possuem alguma memória, esse tipo de modelagem pode ser de grande ajuda nos seus exercícios econométricos.
Nesse contexto, para termos condições de modelar e gerar previsões nessa abordagem, vamos ver alguns conceitos básicos e importantes para prosseguirmos. Em seguida, aprenderemos a analisar as famosas funções de autocorrelação, reconheceremos os termos AR e MA de um processo ARMA, aprenderemos a identificar o problema da não estacionariedade e apresentaremos, por fim, a metodologia proposta por Box et al. (2016) para construir previsões a partir de modelos univariados.
ARIMA
Estaremos interessados em modelos que possam ser representados da forma
(1)
Onde é um ruído branco. Para o caso em que
, teremos modelos como
(2)
Onde quem irá dizer se o processo é ou não estacionário será o valor de
:
(i) se , o processo é estacionário;
(ii) se , o processo será não estacionário.
Processo Autoregressivo
Suponha que tenhamos um processo como
{#eq-ar1b} Onde . Como vimos, a trajetória desse processo depende de
. Se
, os choques se acumulam ao longo do tempo, formando assim um processo não estacionário.
Por enquanto, entretanto, vamos considerar o caso em que , de modo que tenhamos um processo estacionário. Assim, aplicando o operador defasagem à equação acima, temos que:
Obs. O operador defasagem é definido como .
O processo descrito pela equação @eq-ar1l é conhecido na literatura como **processo autoregressivo de primeira ordem**, bastante útil na modelagem e previsão de séries onde a primeira defasagem possui significância estatística.
Processo de Média Móvel
Assumindo estacionariedade fraca, como posto em @tsay2, nós temos que ,
e
, onde
,
são constantes e
é uma função de
, independente do tempo.
Dito isso, podemos obter a média e a variância da série como segue. Tomando o valor esperado sobre a equação @{eq-ar1b} nós obtemos
(3)
Sob as condições de estacionariedade, e, consequentemente,
(4)
Esse resultado tem duas implicações para .
Primeiro, a média de existe se
.
Segundo, a média de será zero se (e apenas se)
.
Agora, considerando o processo AR(1) pode ser reescrito como
{#eq-eq21}
Fazendo repetidas substituições, a equação anterior implica que
(5)
Ou seja, transformamos um **processo autoregressivo** em um processo de **média móvel**.
Um processo MA(1) é representado como abaixo:
(6)
onde é um ruído branco e
e
podem ser quaisquer constantes.
Processos ARMA(p, q)
Agora que temos uma noção do que são processos autoregressivos e de média móveis, podemos juntar os dois. Desta forma podemos analisar processos mistos, ou processos **ARMA**. Este processo, **ARMA(p,q)**, mais geral pode ser formulado como a seguir
(7)
ARIMA (p, d, q)
Quando temos um processo que não necessita de diferenciação a chamamos de **processo integrado de ordem 0** ou alternativamente um **processo I(0)**.
Um segundo caso vem à tona quando é preciso **diferenciar** a série em questão para torná-la estacionária. Isto é, devemos aplicar o operador diferença sobre
.
Nesse caso, se precisamos diferenciar a série uma vez para torná-la estacionária, refere-se à mesma como sendo um **processo integrado de ordem 1** ou alternativamente um **processo I(1)**.
[^3]: Em termos de operador defasagem, ou genericamente,
, onde
será o número de vezes que a série foi diferenciada.
No contexto da modelagem discutida anteriormente, significa dizer que teremos agora um processo **autorregressivo integrado de médias móveis**
, onde
refere-se à ordem de integração, isto é, ao número de vezes que a série
precisou ser diferenciada para que a mesma se tornasse estacionária.
SARIMA (p, d, q)(P, D, Q)m
Os modelos ARIMA também são capazes de modelar uma ampla gama de dados sazonais.
Um modelo ARIMA sazonal é formado pela inclusão de termos sazonais adicionais, na forma , onde o segundo componente faz referência à parte sazonal e
significa o número de períodos por estação.
Estimação e Seleção de ordem
Estimação
Uma vez que a ordem do modelo tenha sido identificada (ou seja, os valores de p, d e q), precisamos estimar os parâmetros .
O processo usual é a Estimação de Máxima Verossimilhança (MLE, na sigla em inglês).
Essa técnica encontra os valores dos parâmetros que maximizam a probabilidade de obter os dados que observamos.
Na prática, pacotes e funções (que contém o algoritmo de estimação) reportarão o valor do logaritmo da verossimilhança dos dados; ou seja, o logaritmo da probabilidade dos dados observados serem provenientes do modelo estimado.
Para valores dados de p, d e q, o algoritmo tentará maximizar o logaritmo da verossimilhança ao encontrar as estimativas dos parâmetros.
Critérios de Informação
Os Critérios de Informação são úteis para avaliar e comparar modelos da mesma classe, porém, com escolhas diferentes. São bastante utilizados em modelos ARIMA, como forma de comparar as estimavativas com base em diferentes ordens dos processos.
A ideia é que os critérios sejam os menores possíveis, e com essa possibilidade, há algoritmos que possibilitam escolher o número de ordens de uma modelo tal que minimize os critérios, como é o caso do Auto ARIMA.
Critério de Informação de Akaike (AIC)
onde é a verossimilhança dos dados,
se
e
se
.
Observe que o último termo entre parênteses é o número de parâmetros no modelo (incluindo , a variância dos resíduos).
Critério de Informação de Akaike corrigido (AICc)
Para modelos ARIMA, o AICc é descrito como:
Para valores pequenos de T, o AIC tende a selecionar um número excessivo de preditores, e, portanto, uma versão corrigida do AIC foi desenvolvida.
Critério de Informação Bayesiano de Schwarz
O Critério de Informação Bayesiano de Schwarz (geralmente abreviado como BIC, SBIC ou SC):
O BIC penaliza o número de parâmetros com mais rigor do que o AIC
Bons modelos são obtidos minimizando o AIC, AICc ou BIC. Nossa preferência é usar o AICc.
É importante observar que esses critérios de informação geralmente não são bons guias para selecionar a ordem adequada de diferenciação (d) de um modelo, mas apenas para selecionar os valores de p e q.
Isso ocorre porque a diferenciação altera os dados nos quais a verossimilhança é calculada, tornando os valores de AIC entre modelos com diferentes ordens de diferenciação não comparáveis. Portanto, precisamos usar outra abordagem para escolher d e, em seguida, podemos usar o AICc para selecionar p e q.
Metodologia Box-Jenkins
Uma vez que tenhamos chegado a modelos representados por um ARIMA ou SARIMA, podemos agora assim apresentar a metodologia proposta por Box et al. (2016) de modo a consolidar nossa análise univariada de séries temporais.
A metodologia Box-Jenkins é composta por quatro etapas principais:
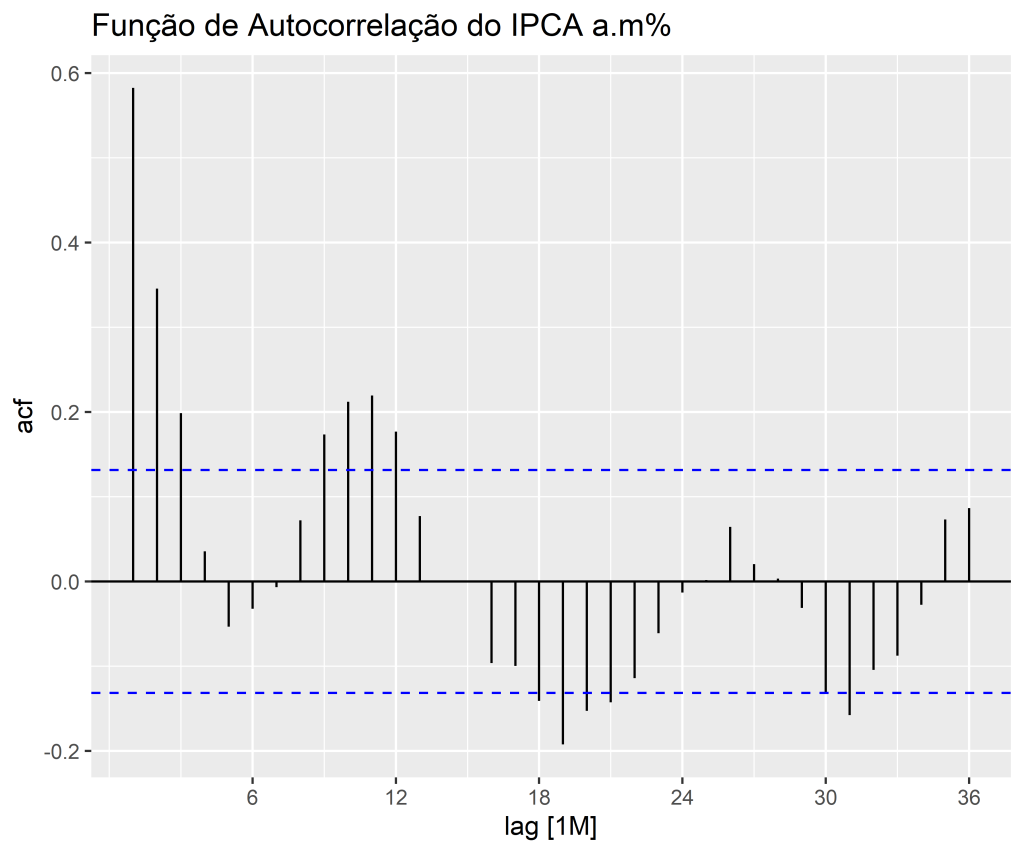
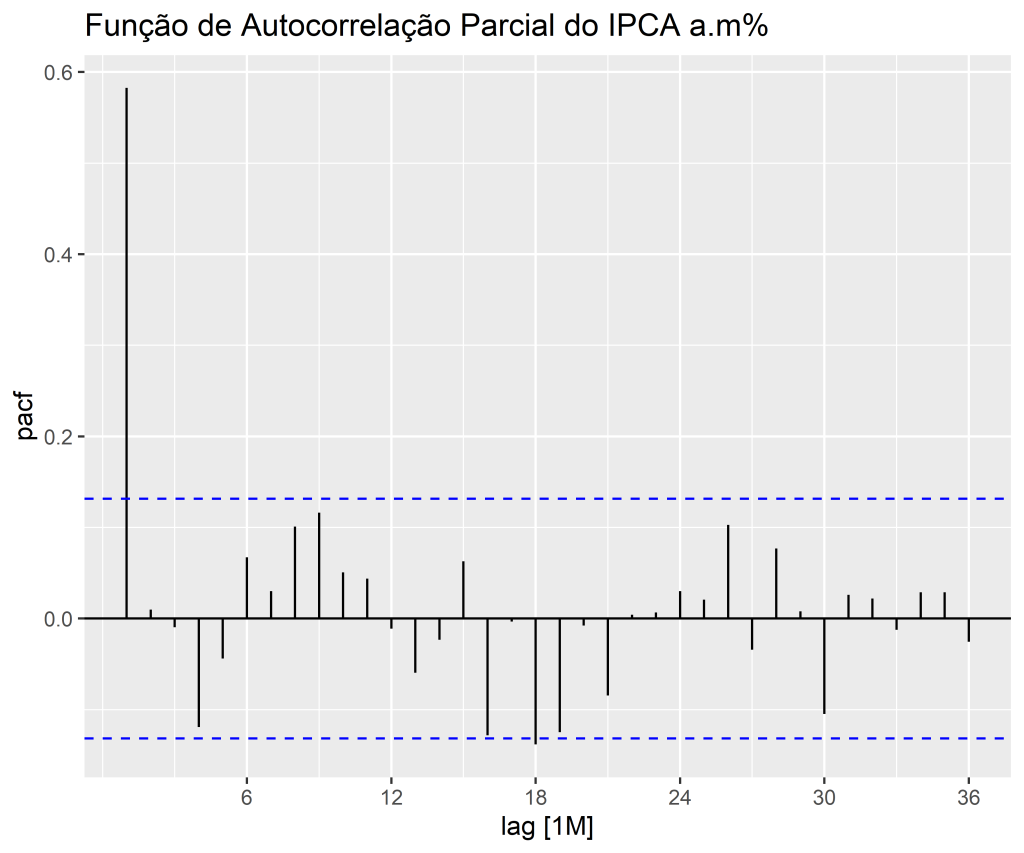
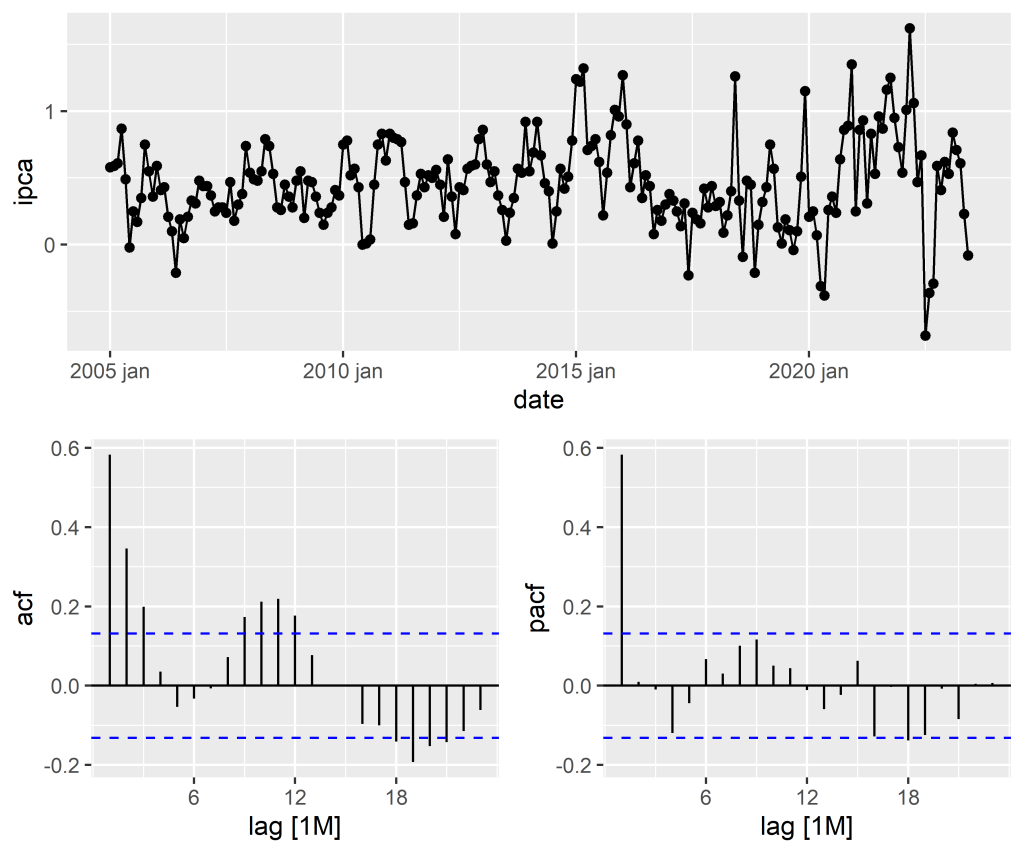
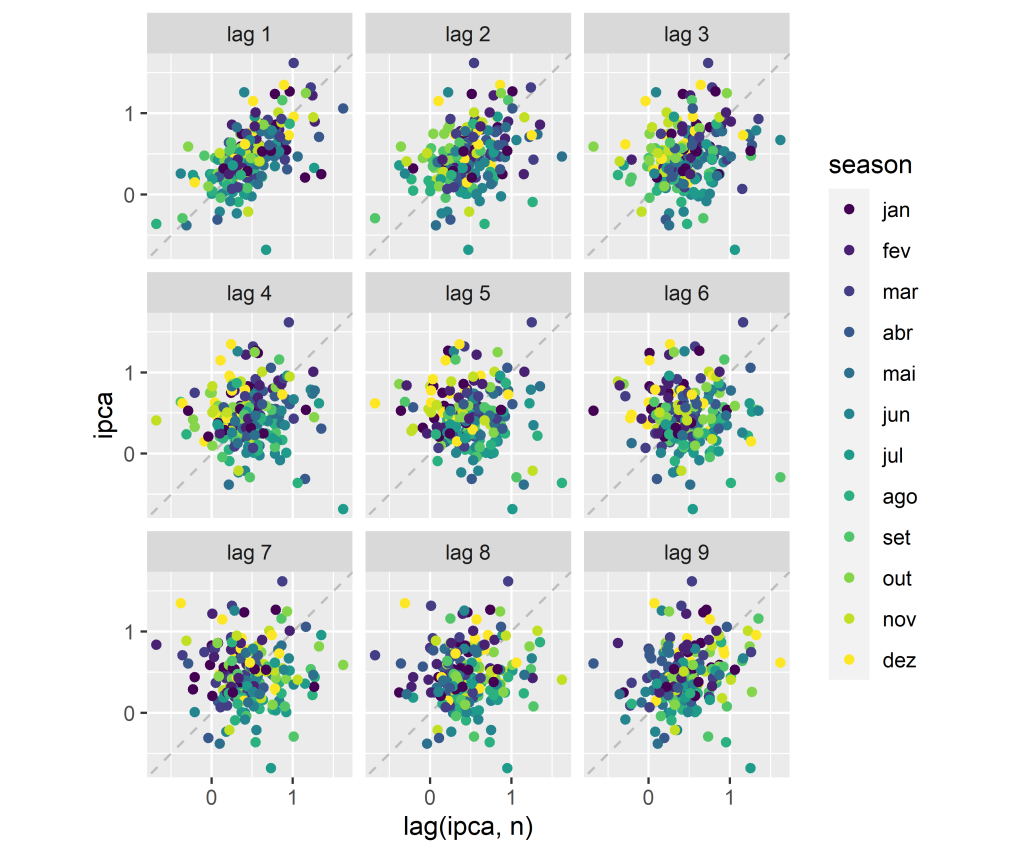
1. Identificação do Modelo: Nesta etapa, a série temporal é analisada para identificar seus padrões, como tendência, sazonalidade e componentes de erro. Os gráficos de autocorrelação e autocorrelação parcial são utilizados para identificar os termos autorregressivos (AR) e de média móvel (MA) que podem estar presentes no modelo. Além disso, o uso de diferenciação pode ser necessário para tornar a série temporal estacionária.
2. Estimação do Modelo: Após a identificação do modelo, os parâmetros são estimados usando técnicas de estimativa, como o método dos mínimos quadrados ou a máxima verossimilhança. A seleção do modelo adequado pode ser baseada em critérios de informação, como o Critério de Informação de Akaike (AIC) ou o Critério de Informação Bayesiano (BIC). Também é útil avaliar o número de coeficientes significativos.
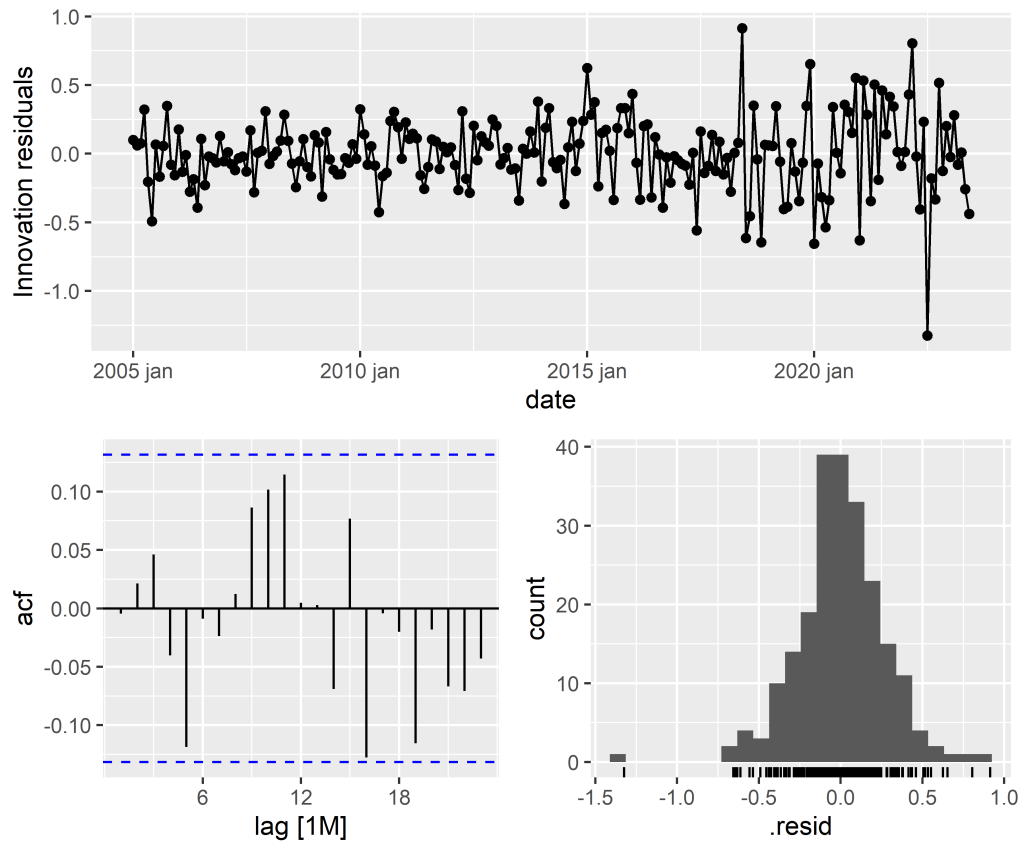
3. Diagnóstico do Modelo: Nesta etapa, o modelo estimado é avaliado por meio da análise dos resíduos. Os resíduos devem ser independentes, não apresentar autocorrelação significativa e ter distribuição normal. Os testes de diagnóstico, como o teste de Ljung-Box, podem ser usados para verificar a presença de autocorrelação nos resíduos.
4. Previsão: Uma vez escolhido o melhor modelo, passa-se à etapa de previsão.
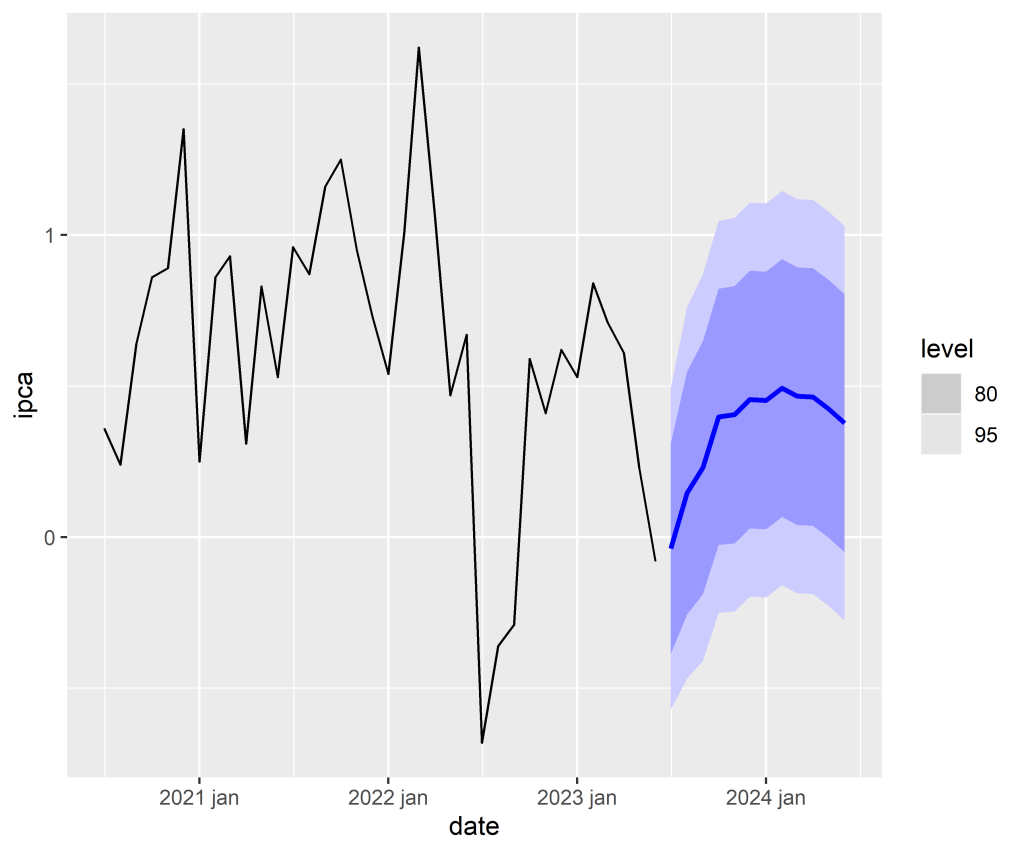
Exemplo: Modelagem e Previsão do IPCA
Abaixo, temos um processo que segue o exposto por Box-Jenkins. Iremos realizar a previsão do IPCA a.m% por meio de um modelo ARIMA.
1. Identificação do Modelo
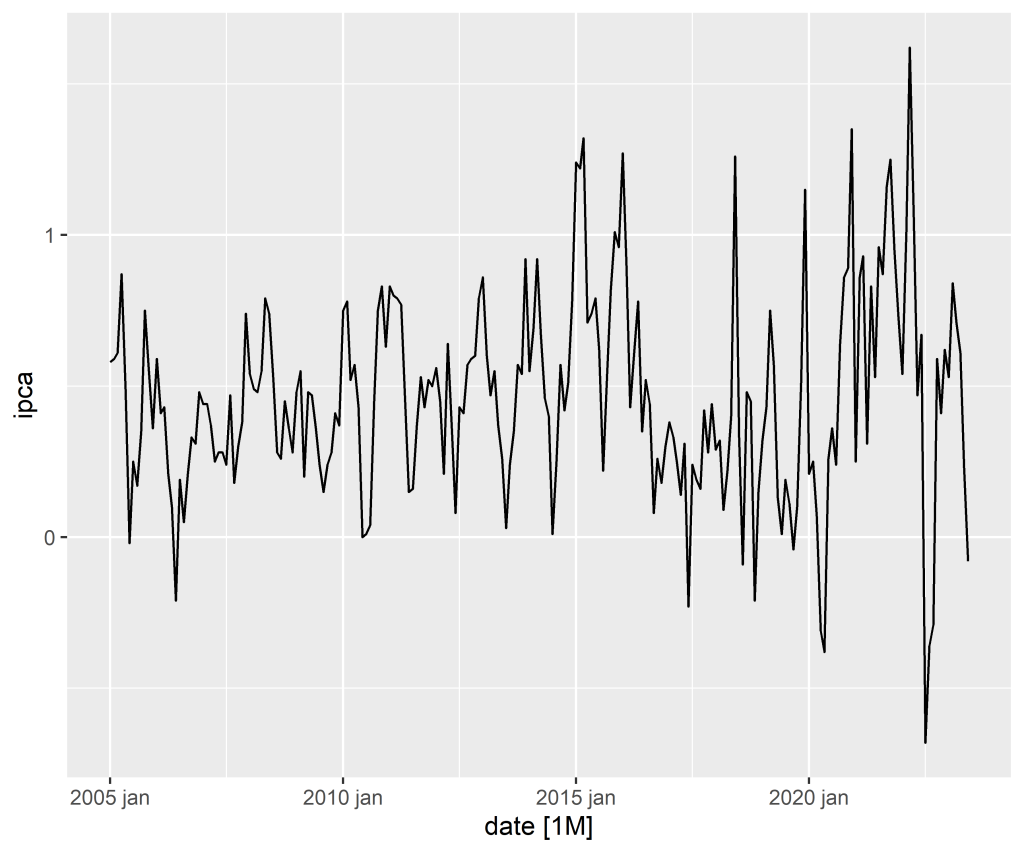
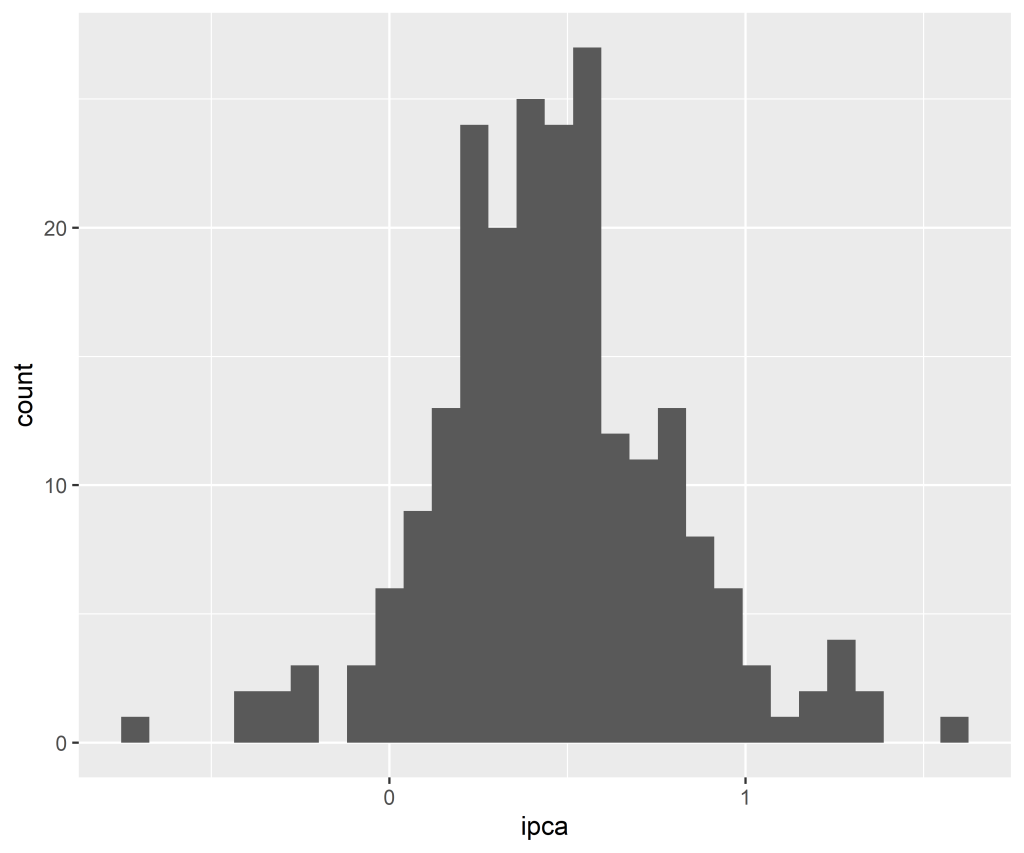
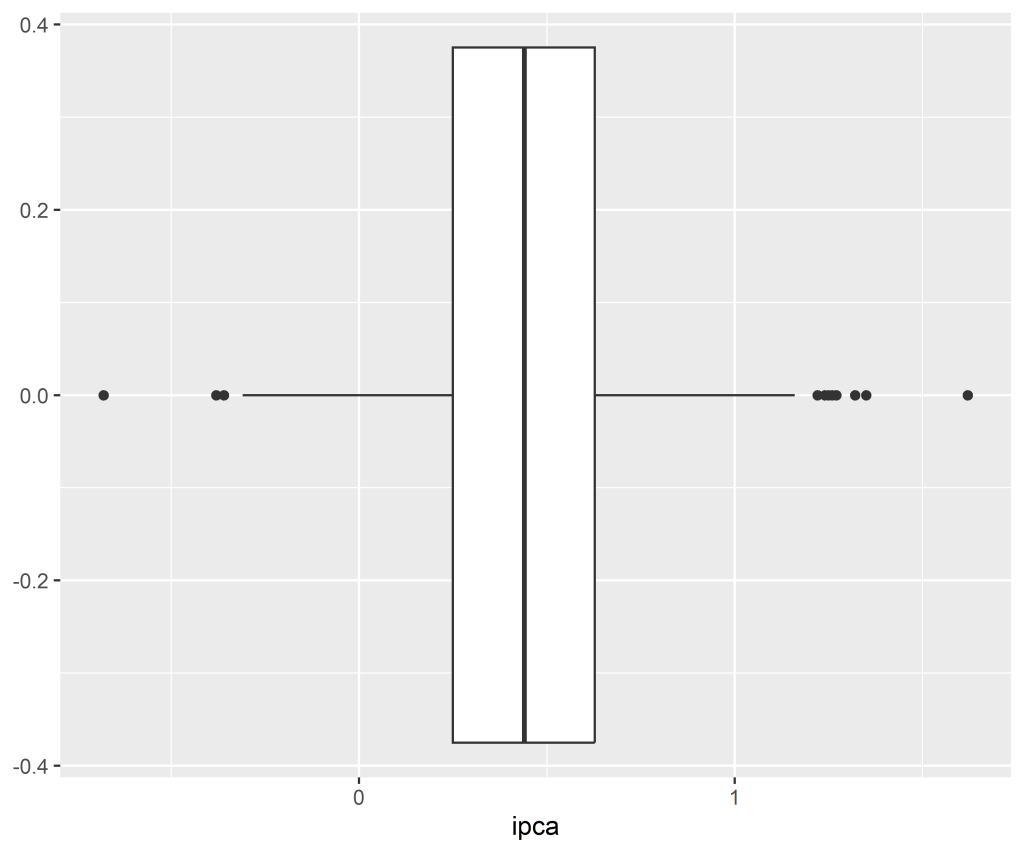
1.1 Verificando a distribuição, tendência e sazonalidade
Código
1.2 Verificando a estacionariedade
Código
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -4.18 0.01
[2,] 1 -3.48 0.01
[3,] 2 -3.06 0.01
[4,] 3 -3.07 0.01
[5,] 4 -2.71 0.01
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -7.46 0.01
[2,] 1 -6.55 0.01
[3,] 2 -6.05 0.01
[4,] 3 -6.35 0.01
[5,] 4 -6.06 0.01
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -7.47 0.01
[2,] 1 -6.57 0.01
[3,] 2 -6.07 0.01
[4,] 3 -6.41 0.01
[5,] 4 -6.11 0.01
----
Note: in fact, p.value = 0.01 means p.value <= 0.01 Código
KPSS Unit Root Test
alternative: nonstationary
Type 1: no drift no trend
lag stat p.value
3 4.45 0.01
-----
Type 2: with drift no trend
lag stat p.value
3 0.0893 0.1
-----
Type 1: with drift and trend
lag stat p.value
3 0.0638 0.1
-----------
Note: p.value = 0.01 means p.value <= 0.01
: p.value = 0.10 means p.value >= 0.10 Código
ndiffs
0 Código
nsdiffs
0 2. Estimação do Modelo
Código
Código
| .model | term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|---|
| arima_auto | ar1 | 0.5775190 | 0.0552453 | 10.4537248 | 0.0000000 |
| arima_auto | sma1 | 0.1393787 | 0.0714066 | 1.9519032 | 0.0522072 |
| arima_auto | constant | 0.1929235 | 0.0203892 | 9.4620286 | 0.0000000 |
| arima100 | ar1 | 0.5775190 | 0.0552453 | 10.4537248 | 0.0000000 |
| arima100 | sma1 | 0.1393787 | 0.0714066 | 1.9519032 | 0.0522072 |
| arima100 | constant | 0.1929235 | 0.0203892 | 9.4620286 | 0.0000000 |
| arima001 | ma1 | 0.4752090 | 0.0498495 | 9.5328778 | 0.0000000 |
| arima001 | sma1 | 0.1537124 | 0.0739462 | 2.0787061 | 0.0387934 |
| arima001 | constant | 0.4586221 | 0.0321676 | 14.2572589 | 0.0000000 |
| arima002 | ma1 | 0.5440458 | 0.0657682 | 8.2721680 | 0.0000000 |
| arima002 | ma2 | 0.2228784 | 0.0568446 | 3.9208362 | 0.0001176 |
| arima002 | sma1 | 0.1659500 | 0.0722557 | 2.2967055 | 0.0225679 |
| arima002 | constant | 0.4578569 | 0.0376409 | 12.1637992 | 0.0000000 |
| arima003 | ma1 | 0.5398217 | 0.0659356 | 8.1871065 | 0.0000000 |
| arima003 | ma2 | 0.3185256 | 0.0655897 | 4.8563345 | 0.0000023 |
| arima003 | ma3 | 0.1961174 | 0.0683263 | 2.8703082 | 0.0044971 |
| arima003 | sma1 | 0.1284788 | 0.0720572 | 1.7830102 | 0.0759510 |
| arima003 | constant | 0.4573402 | 0.0416444 | 10.9820219 | 0.0000000 |
| arima101 | ar1 | 0.5901232 | 0.0913666 | 6.4588484 | 0.0000000 |
| arima101 | ma1 | -0.0189901 | 0.1114335 | -0.1704160 | 0.8648382 |
| arima101 | sma1 | 0.1397312 | 0.0714514 | 1.9556120 | 0.0517655 |
| arima101 | constant | 0.1871272 | 0.0200028 | 9.3550492 | 0.0000000 |
| arima102 | ar1 | 0.5639163 | 0.1279138 | 4.4085642 | 0.0000162 |
| arima102 | ma1 | 0.0036002 | 0.1368155 | 0.0263145 | 0.9790301 |
| arima102 | ma2 | 0.0297141 | 0.0936972 | 0.3171287 | 0.7514440 |
| arima102 | sma1 | 0.1406951 | 0.0714781 | 1.9683650 | 0.0502706 |
| arima102 | constant | 0.1991270 | 0.0210872 | 9.4430090 | 0.0000000 |
| arima103 | ar1 | 0.3773364 | 0.2040486 | 1.8492474 | 0.0657515 |
| arima103 | ma1 | 0.1848540 | 0.2021046 | 0.9146452 | 0.3613703 |
| arima103 | ma2 | 0.1465525 | 0.1211616 | 1.2095619 | 0.2277335 |
| arima103 | ma3 | 0.1289802 | 0.0873118 | 1.4772374 | 0.1410292 |
| arima103 | sma1 | 0.1243380 | 0.0722531 | 1.7208665 | 0.0866683 |
| arima103 | constant | 0.2841689 | 0.0292971 | 9.6995434 | 0.0000000 |
Código
| .model | n_coeficientes | n_significativos | perc_significativos |
|---|---|---|---|
| arima103 | 6 | 1 | 16.66667 |
| arima102 | 5 | 2 | 40.00000 |
| arima101 | 4 | 2 | 50.00000 |
| arima100 | 3 | 2 | 66.66667 |
| arima_auto | 3 | 2 | 66.66667 |
| arima003 | 5 | 4 | 80.00000 |
| arima001 | 3 | 3 | 100.00000 |
| arima002 | 4 | 4 | 100.00000 |
Código
| .model | sigma2 | log_lik | AIC | AICc | BIC |
|---|---|---|---|---|---|
| arima_auto | 0.0738393 | -24.56393 | 57.12785 | 57.31218 | 70.73856 |
| arima100 | 0.0738393 | -24.56393 | 57.12785 | 57.31218 | 70.73856 |
| arima101 | 0.0741679 | -24.54951 | 59.09903 | 59.37681 | 76.11242 |
| arima102 | 0.0744748 | -24.49990 | 60.99980 | 61.39050 | 81.41587 |
| arima103 | 0.0742154 | -23.59176 | 61.18351 | 61.70688 | 85.00225 |
| arima003 | 0.0746812 | -24.78193 | 61.56386 | 61.95456 | 81.97992 |
| arima002 | 0.0769260 | -28.60979 | 67.21957 | 67.49735 | 84.23296 |
| arima001 | 0.0816666 | -35.69829 | 79.39659 | 79.58092 | 93.00730 |
3. Diagnóstico do Modelo
4. Previsões
4.1 Restrição da amostra (teste e treino)
4.2 Acurácia
Código
| .model | .type | ME | RMSE | MAE | MPE | MAPE | MASE | RMSSE | ACF1 |
|---|---|---|---|---|---|---|---|---|---|
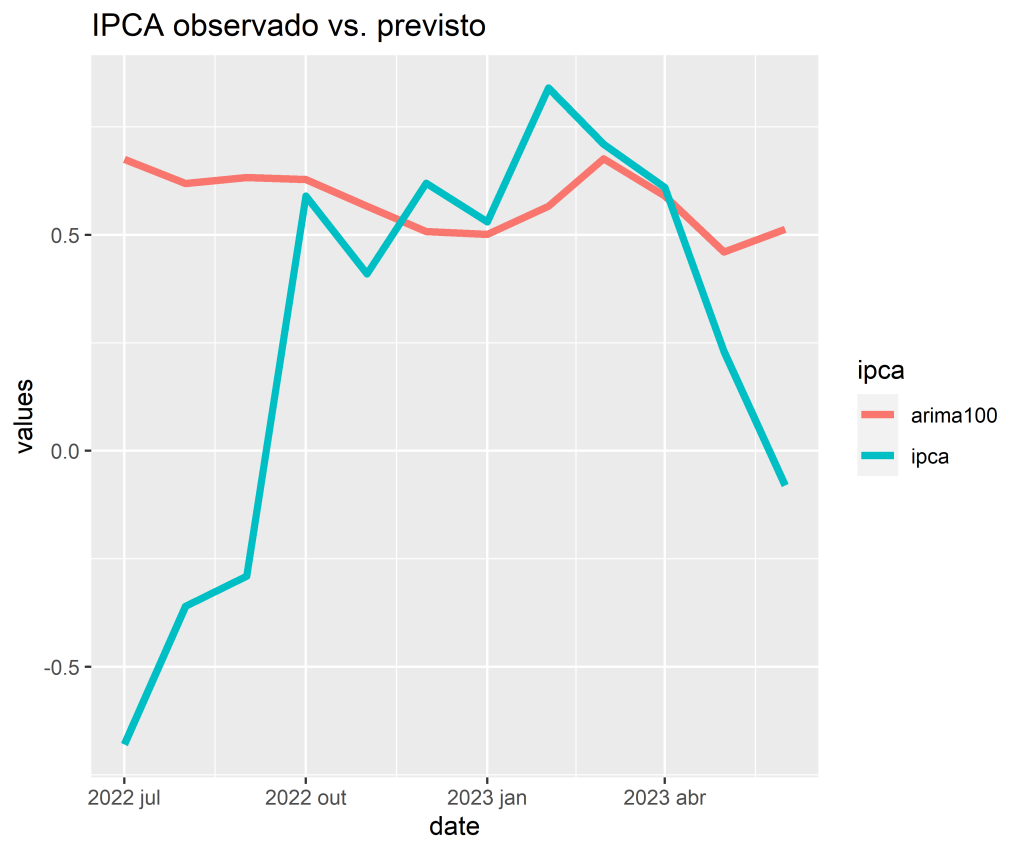
| arima100 | Test | -0.3171952 | 0.5891764 | 0.3952224 | 120.8467 | 144.9853 | NaN | NaN | 0.5801309 |
4.3 Previsão Fora da Amostra
___________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.
Referências
Hyndman, R. J., e G. Athanasopoulos. 2013. Forecasting: Principles and Practice. OTexts.