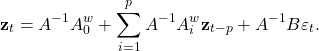No post de hoje, vamos abordar os modelos lineares multivariados, apresentando conceitos importantes por meio de simulações e gráficos criados por meio das linguagens R e Python. Nosso objetivo é proporcionar uma compreensão clara e acessível desses modelos, de modo que seja fácil de entender e acompanhar. Nesta parte, apresentamos o modelo VAR e SVAR.
Na seção anterior, consideramos a análise univariada de séries temporais, em que nosso objetivo era, basicamente, entender a dependência dinâmica de uma série , isto é, a dependência de
com os seus valores passados
.
Pode ser interessante, entretanto, considerar simultaneamente duas ou mais séries. Por exemplo, o nível de ociosidade da economia certamente tem influência sobre a taxa de crescimento dos preços, assim como um aumento da taxa de juros tem relação com a taxa de desemprego. Ademais, pode ser necessário em algumas ocasiões avaliar o quanto um choque em afeta
.
Essas questões, bastante pertinentes no dia a dia, são tratadas dentro do que chamamos de análise multivariada de séries temporais.
São objetivos básicos da análise multivariada de séries temporais:
- Estudar as relações dinâmicas entre séries diversas;
- Melhorar as previsões sobre uma variável específica.
Seja um vetor de dimensão
que contém séries temporais observadas em um período de tempo comum. Por exemplo,
é o PIB trimestral brasileiro e
é a taxa de desemprego também trimestral.
Para obter todo o código do processo de criação dos gráficos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Acaso, estudemos e
conjuntamente poderemos verificar a dependência contemporânea e passada que existe entre essas duas variáveis. Poderemos verificar o quanto um choque no PIB afeta a taxa de desemprego e quanto tempo isso tende a durar. Analogamente, podemos estar interessados na relação entre a taxa de desemprego e a inflação.
Código
| desemprego | inflacao | |
|---|---|---|
| desemprego | 1.00000 | -0.29277 |
| inflacao | -0.29277 | 1.00000 |
A correlação entre as variáveis é elevada, mas isso, claro, não é o bastante para identificarmos a natureza da relação entre elas.
Algumas questões devem ser levadas em consideração. Em primeiro lugar, para uma análise econométrica, precisamos definir se as séries são estacionárias. Essa primeira (grande) questão definirá o tipo de análise que faremos entre elas. Vamos supor que elas sejam estacionárias.
Podemos, nesse caso, estimar um Vetor Autoregressivo de primeira ordem, de modo que:
(1)
O VAR(1) vai descrever a evolução dinâmica da interação entre a inflação e desemprego. Uma vez estimado esse modelo, poderemos nos perguntar se existe causalidade nessa relação, isto é, se inflação de fato ajuda a prever o desemprego, se o contrário ocorre ou se há uma simultaneidade. Nesse último caso, dizemos que existe uma causalidade bidirecional.
Ademais, esse tipo de análise também irá nos permitir estimar funções de impulso-resposta, onde analisamos a resposta a impulsos em uma das variáveis. Por exemplo, um choque no desemprego tem qual efeito sobre a inflação? E o caso contrário? Uma análise como essa pode ser muito interessante para avaliar a relação que existe entre duas ou mais variáveis, não é mesmo?
Um dos pressupostos, entretanto, do modelo acima é que as variáveis sejam estacionárias, no sentido que discutimos anteriormente.
Isso significa que se essa hipótese for violada, teremos que partir para outro tipo de análise. Discutiremos a existência de cointegração entre duas ou mais variáveis, isto é, para o caso em que lidamos com séries não estacionárias, pode ser o caso de nos perguntarmos se existe uma relação entre de longo-prazo entre elas.
Para o exemplo acima, se as séries não forem estacionárias, como de fato aparentam não ser, as mesmas podem estar relacionadas ao longo do tempo. Se for esse o caso, dizemos que as séries possuem uma tendência comum, o que nos permite avaliar a relação entre elas ao longo do tempo.
Veremos portanto os modelos multivariados estacionários, com ênfase na construção de vetores autorregressivos. Na sequência, tratamos de modelos multivariados não estacionários, com ênfase no conceito de cointegração e na estimação de um vetor de correção de erros.
Modelos multivariados estacionários
Processos autorregressivos de média móvel (ARMA) podem ser facilmente estendidos para o caso multivariado, onde o processo estocástico que gera um vetor de séries temporais é modelado.
O mais comum dentre eles é o vetor autorregressivo (VAR), isto porque pode ser facilmente estimado via mínimos quadrados ordinários ou método bayesiano, as suas propriedades têm sido extensivamente estudadas na literatura e também porque são bastante similares às regressões lineares múltiplas.^[Ver @tsay.]
Um VAR irá descrever a evolução dinâmica de um determinado número de variáveis de acordo com a história comum entre elas. Para ilustrar, considere um vetor autorregressivo de ordem 1, como
(2)
onde e
são ruídos brancos independentes das estórias de
e
, mas que podem estar correlacionados.
Se, por exemplo, , significa dizer que a estória de
ajuda a explicar
. O sistema acima, a propósito, pode ser representando da seguinte forma, como faz @tsay:
(3)
Ou, ainda, como
Esse sistema de ordem 1, a propósito, pode ser generalizado para qualquer ordem como
onde para
é uma vetor
contendo observações de
séries temporais,
é um vetor
de interceptos,
é uma matriz
de coeficientes e
é um vetor
de erros, independentes e identicamente distribuídos, com média zero e covariância igual a
.
É conveniente representar o VAR com a utilização do operador defasagem como
(4)
Estabilidade do VAR
Assim como vimos para os modelos univariados, é preciso considerar uma condição de estacionariedade ou, de forma análoga, estabilidade para o vetor autorregressivo.
Podemos verificar isso ao considerar o polinômio característico reverso
(5)
Nesse caso, se a solução para a equação acima tem uma raiz para , uma ou todas as variáveis do
são processos integrados de ordem 1. Nesse caso, o sistema não será estável.
Na prática, podemos ver a estabilidade do VAR calculando os autovalores da matriz de coeficientes. Se o módulo dos autovalores da matriz forem menores do que a unidade, o processo é dito estável.
Estimação
Para ilustrar, vamos considerar um exemplo envolvendo algumas variáveis bastante conhecidas:
(i) inflação mensal medida pelo IPCA;
(ii) expectativas em para
para a taxa de inflação mensal;
(iii) número índice da produção industrial;
(iv) taxa de câmbio R$/US$;
(v) taxa Selic anualizada;
(vi) taxa de desemprego medida pela PNAD Contínua ajustada para todo o período.
Código
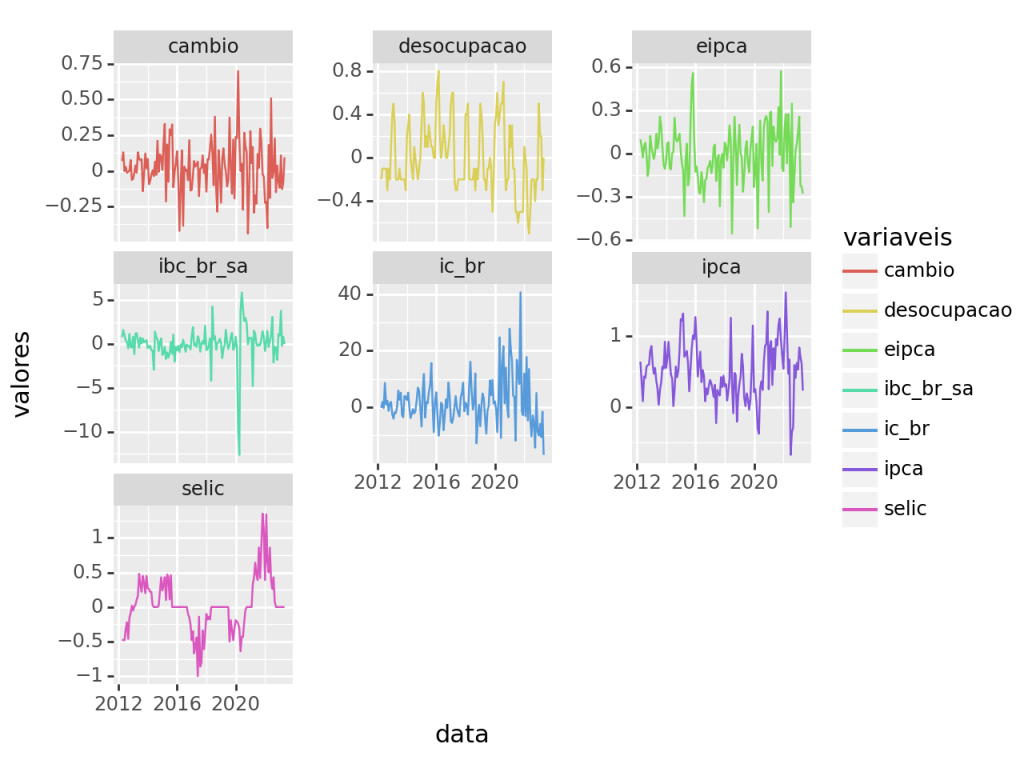
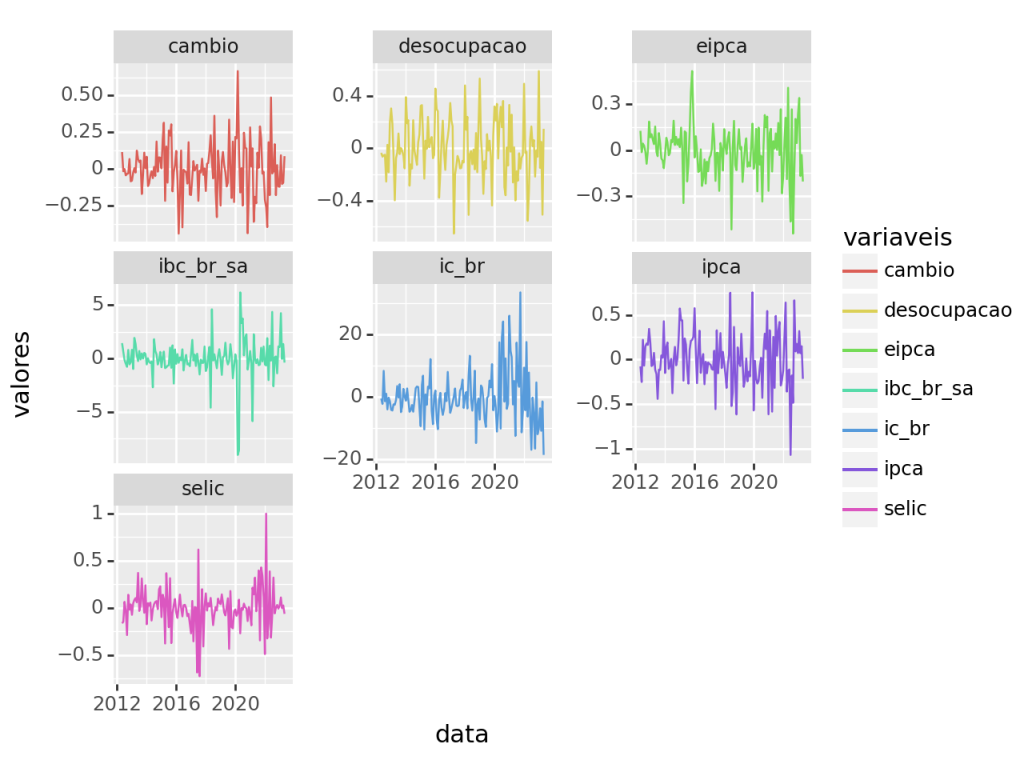
Um ponto importante que devemos nos atentar, para garantir a estabilidade do modelo, é a estacionariedade das séries. O gráfico abaixo deixa isso mais claro.
Acaso o leitor aplique o Teste ADF visto na seção anterior, verá que algumas de nossas séries não são estacionárias. Isso, como vimos, pode ser um problema para a estabilidade do nosso VAR.
Teste de Dickey-Fuller Aumentado em "ipca"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -5.9919
Número de Lags Escolhidos = 0
Valor Crítico 1% = -3.48
Valor Crítico 5% = -2.883
Valor Crítico 10% = -2.578
=> Valor-P = 0.0. Rejeitando a Hipótese Nula.
=> A série é Estacionária.
Teste de Dickey-Fuller Aumentado em "desocupacao"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -1.827
Número de Lags Escolhidos = 13
Valor Crítico 1% = -3.486
Valor Crítico 5% = -2.886
Valor Crítico 10% = -2.58
=> Valor-P = 0.3672. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
Teste de Dickey-Fuller Aumentado em "eipca"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -1.706
Número de Lags Escolhidos = 11
Valor Crítico 1% = -3.485
Valor Crítico 5% = -2.885
Valor Crítico 10% = -2.579
=> Valor-P = 0.428. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
Teste de Dickey-Fuller Aumentado em "cambio"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -1.2041
Número de Lags Escolhidos = 0
Valor Crítico 1% = -3.48
Valor Crítico 5% = -2.883
Valor Crítico 10% = -2.578
=> Valor-P = 0.6718. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
Teste de Dickey-Fuller Aumentado em "selic"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -1.5635
Número de Lags Escolhidos = 9
Valor Crítico 1% = -3.484
Valor Crítico 5% = -2.885
Valor Crítico 10% = -2.579
=> Valor-P = 0.5019. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
Teste de Dickey-Fuller Aumentado em "ic_br"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -2.0476
Número de Lags Escolhidos = 8
Valor Crítico 1% = -3.483
Valor Crítico 5% = -2.885
Valor Crítico 10% = -2.579
=> Valor-P = 0.2661. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
Teste de Dickey-Fuller Aumentado em "ibc_br_sa"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -2.1514
Número de Lags Escolhidos = 2
Valor Crítico 1% = -3.481
Valor Crítico 5% = -2.884
Valor Crítico 10% = -2.579
=> Valor-P = 0.2243. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
Assim, de modo a contornar o problema, vamos simplesmente diferenciar as séries que consideramos não estacionárias. Isso é feito abaixo.
Vejamos agora o resultado visual das séries diferenciadas.
Agora nossos dados estão prontos para o uso.
Estimando o modelo VAR
Para estimar o VAR, podemos utilizar os módulos e funções presentes na biblioteca `statsmodels`, especificamente `statsmodels.tsa.api`.
Determinação da ordem de defasagem
Uma vez de posse dos nossos dados, já devidamente tratados, um problema imediato é determinar a ordem de defasagem do nosso modelo.
Isso é feito empiricamente pela análise de critérios de informação. Os mais conhecidos são os critérios de Akaike, Hannan-Quinn e Schwarz.
(6)
onde
(7)
No Python esses critérios estão implementados na função VAR de forma automática, isto é, a função estimará o modelo com a defasagem escolhida de acordo com o critério selecionado no parâmetro ic do método fit do VAR (padrão é aic).
Alternativamente, é possível escolher o número máximo de defasagens no método fit pelo parâmetro maxlags.
De modo a escolher um modelo mais parcimonioso, vamos optar aqui por maxlags=1 (que seria a ordem escolhida pelo critério aic).
Isso porque, digamos que estamos interessados em analisar a trajetória da inflação mensal. Como a mesma apresenta sazonalidade, é importante ressaltar isso em nosso modelo.
Abaixo, podemos ver o modelo estimado
Código
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Mon, 26, Jun, 2023
Time: 16:53:32
--------------------------------------------------------------------
No. of Equations: 7.00000 BIC: -8.65340
Nobs: 133.000 HQIC: -9.37585
Log likelihood: -608.651 FPE: 5.17355e-05
AIC: -9.87038 Det(Omega_mle): 3.43729e-05
--------------------------------------------------------------------
Results for equation ipca
=================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------
const 0.268374 0.047179 5.688 0.000
L1.ipca 0.416870 0.080542 5.176 0.000
L1.desocupacao 0.122390 0.088427 1.384 0.166
L1.eipca 0.227317 0.149375 1.522 0.128
L1.cambio -0.295995 0.161840 -1.829 0.067
L1.selic 0.164515 0.080436 2.045 0.041
L1.ic_br 0.010510 0.003375 3.114 0.002
L1.ibc_br_sa 0.008750 0.014007 0.625 0.532
=================================================================================
Results for equation desocupacao
=================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------
const -0.039518 0.036109 -1.094 0.274
L1.ipca 0.102862 0.061644 1.669 0.095
L1.desocupacao 0.640409 0.067678 9.463 0.000
L1.eipca -0.068007 0.114325 -0.595 0.552
L1.cambio -0.061473 0.123865 -0.496 0.620
L1.selic -0.107960 0.061562 -1.754 0.079
L1.ic_br -0.002144 0.002583 -0.830 0.407
L1.ibc_br_sa -0.003090 0.010720 -0.288 0.773
=================================================================================
Results for equation eipca
=================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------
const 0.068732 0.026526 2.591 0.010
L1.ipca -0.183772 0.045285 -4.058 0.000
L1.desocupacao -0.028808 0.049718 -0.579 0.562
L1.eipca 0.193463 0.083986 2.304 0.021
L1.cambio -0.095268 0.090994 -1.047 0.295
L1.selic 0.112698 0.045225 2.492 0.013
L1.ic_br 0.009081 0.001898 4.785 0.000
L1.ibc_br_sa 0.013343 0.007875 1.694 0.090
=================================================================================
Results for equation cambio
=================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------
const 0.037214 0.027996 1.329 0.184
L1.ipca -0.026286 0.047794 -0.550 0.582
L1.desocupacao 0.010774 0.052472 0.205 0.837
L1.eipca 0.009699 0.088639 0.109 0.913
L1.cambio -0.029061 0.096035 -0.303 0.762
L1.selic -0.013238 0.047730 -0.277 0.782
L1.ic_br 0.000828 0.002003 0.413 0.679
L1.ibc_br_sa -0.009274 0.008312 -1.116 0.264
=================================================================================
Results for equation selic
=================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------
const -0.062831 0.034780 -1.807 0.071
L1.ipca 0.124161 0.059376 2.091 0.037
L1.desocupacao -0.073999 0.065188 -1.135 0.256
L1.eipca -0.152312 0.110119 -1.383 0.167
L1.cambio 0.074054 0.119307 0.621 0.535
L1.selic 0.731255 0.059297 12.332 0.000
L1.ic_br 0.005417 0.002488 2.177 0.029
L1.ibc_br_sa 0.010913 0.010326 1.057 0.291
=================================================================================
Results for equation ic_br
=================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------
const 0.168084 1.291083 0.130 0.896
L1.ipca 2.441565 2.204088 1.108 0.268
L1.desocupacao -2.326376 2.419852 -0.961 0.336
L1.eipca -1.733609 4.087731 -0.424 0.671
L1.cambio 8.848053 4.428826 1.998 0.046
L1.selic 0.079725 2.201180 0.036 0.971
L1.ic_br 0.096531 0.092365 1.045 0.296
L1.ibc_br_sa -0.414301 0.383303 -1.081 0.280
=================================================================================
Results for equation ibc_br_sa
=================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------
const 0.161448 0.290642 0.555 0.579
L1.ipca -0.324865 0.496173 -0.655 0.513
L1.desocupacao -0.469947 0.544745 -0.863 0.388
L1.eipca -0.163773 0.920209 -0.178 0.859
L1.cambio -2.368373 0.996995 -2.376 0.018
L1.selic -0.421427 0.495519 -0.850 0.395
L1.ic_br 0.061381 0.020793 2.952 0.003
L1.ibc_br_sa 0.187524 0.086287 2.173 0.030
=================================================================================
Correlation matrix of residuals
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
ipca 1.000000 -0.058133 0.463691 -0.094922 0.186900 0.174462 0.001540
desocupacao -0.058133 1.000000 -0.018965 0.020336 -0.075157 -0.038715 -0.047390
eipca 0.463691 -0.018965 1.000000 -0.109849 0.223021 0.125920 -0.030177
cambio -0.094922 0.020336 -0.109849 1.000000 -0.082877 0.240455 -0.250596
selic 0.186900 -0.075157 0.223021 -0.082877 1.000000 0.034758 -0.021288
ic_br 0.174462 -0.038715 0.125920 0.240455 0.034758 1.000000 0.078735
ibc_br_sa 0.001540 -0.047390 -0.030177 -0.250596 -0.021288 0.078735 1.000000Diagnóstico
Uma vez estimado o nosso modelo VAR, a próxima etapa é verificar sua estabilidade. Para começar, verificamos se os módulos dos autovalores são menores do que a unidade. Isso é feito com o código abaixo.
Código
array([-6.69544449-0.j , 1.63723328+2.90944722j,
1.63723328-2.90944722j, 2.95552111+0.95598543j,
2.95552111-0.95598543j, 1.49103399-0.j ,
1.23568305-0.j ])Garantida essa condição, podemos proceder testes clássicos sobre os resíduos do modelo, como o teste de autocorrelação, normalidade e o de heterocedasticidade. O código abaixo ilustra essa análise.
Código
<statsmodels.tsa.vector_ar.hypothesis_test_results.NormalityTestResults at 0x19429483710>Observe que temos problema com os resultados dos testes de autocorrelação e normalidade. Isto é, estamos rejeitando a hipótese nula de ausência de autocorrelação e distribuição normal.
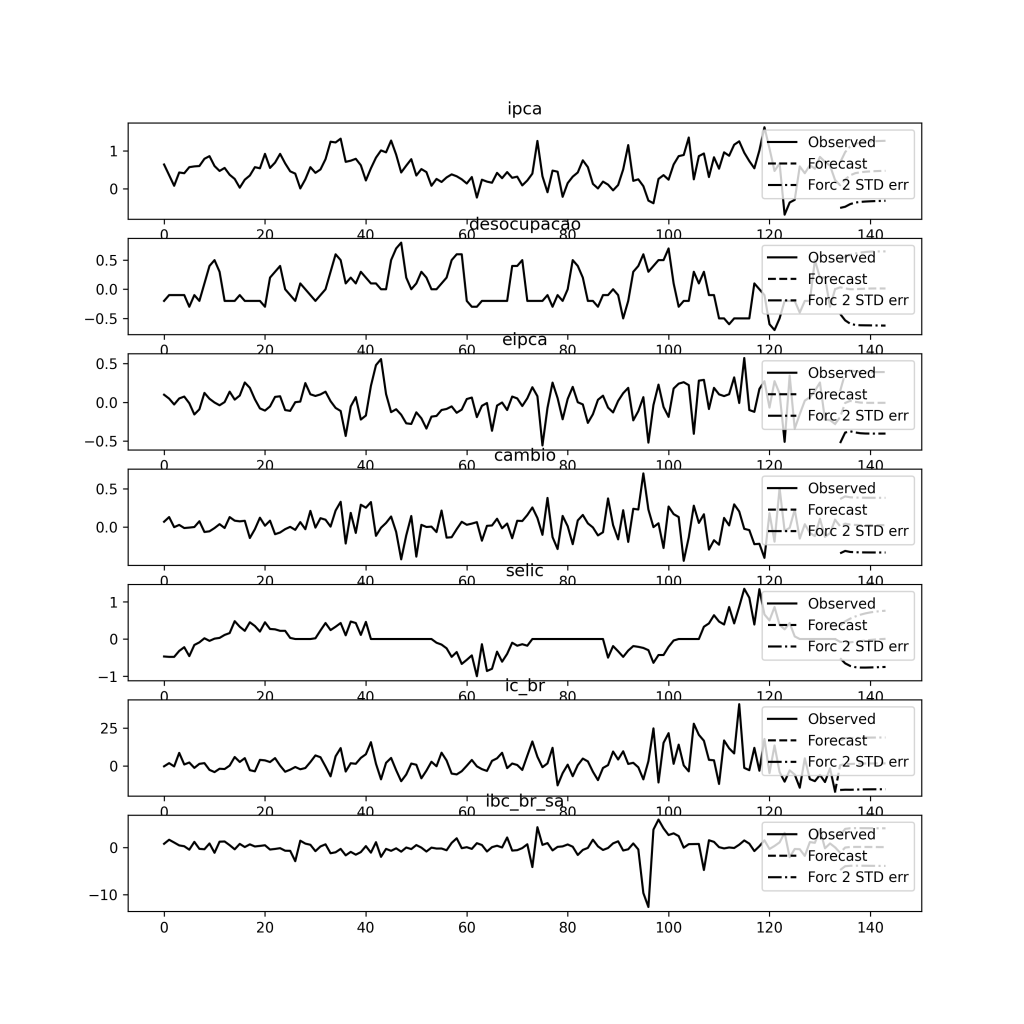
A seguir, podemos ver os gráficos dos resíduos de cada uma das equações estimadas através do comando abaixo.
Por fim, também é importante verificar a estabilidade estrutural do modelo, através da análise do processo de flutuação empírica (EPS, no inglês).
Esse tipo de diagnóstico permite a identificação de mudanças estruturais nas relações analisadas dentro do modelo.
Código
True
Código
array([[ 8.19105949e+00, 2.10667078e+00, 6.90455056e+00,
-1.24789698e+00, 1.24351119e+01, -9.51684249e+00,
2.64841821e+01],
[ 8.05720564e+00, 3.55388563e-01, 1.62578262e+00,
-4.70288779e-01, 8.98494351e+00, -1.86447802e+01,
-2.52310387e+00],
[ 5.43957988e+00, 1.29473028e-02, -2.53261808e-01,
-2.52294227e-01, 7.07055926e+00, 1.19957333e+01,
-7.17959289e+00],
[ 3.78112952e+00, -2.05834988e-01, -1.46263609e-01,
-1.17841160e-01, 5.78848963e+00, 1.63219716e+01,
-4.56252147e+00],
[ 2.90496753e+00, -4.11025534e-01, 1.02427683e-01,
-8.31914901e-02, 4.70690026e+00, 1.30170326e+01,
-2.96027950e+00]])Função Impulso-Resposta
Como vimos no início, a modelagem VAR procura identificar a relação dinâmica existente em um conjunto previamente definido de variáveis. Dentro desse tipo de abordagem, pode ser interessante para o pesquisador verificar o impacto de um choque ou impulso em uma variável sobre as outras.
Esse tipo de exercício é conhecido na literatura como análise de impulso-resposta. A ideia é verificar a resposta esperada na variável da mudança em uma unidade na variável
. Em outras palavras, dá-se um choque em
na variável
e observa-se o efeito desse choque sobre a variável
ao longo de
. Esses efeitos, ademais, podem ser acumulados.
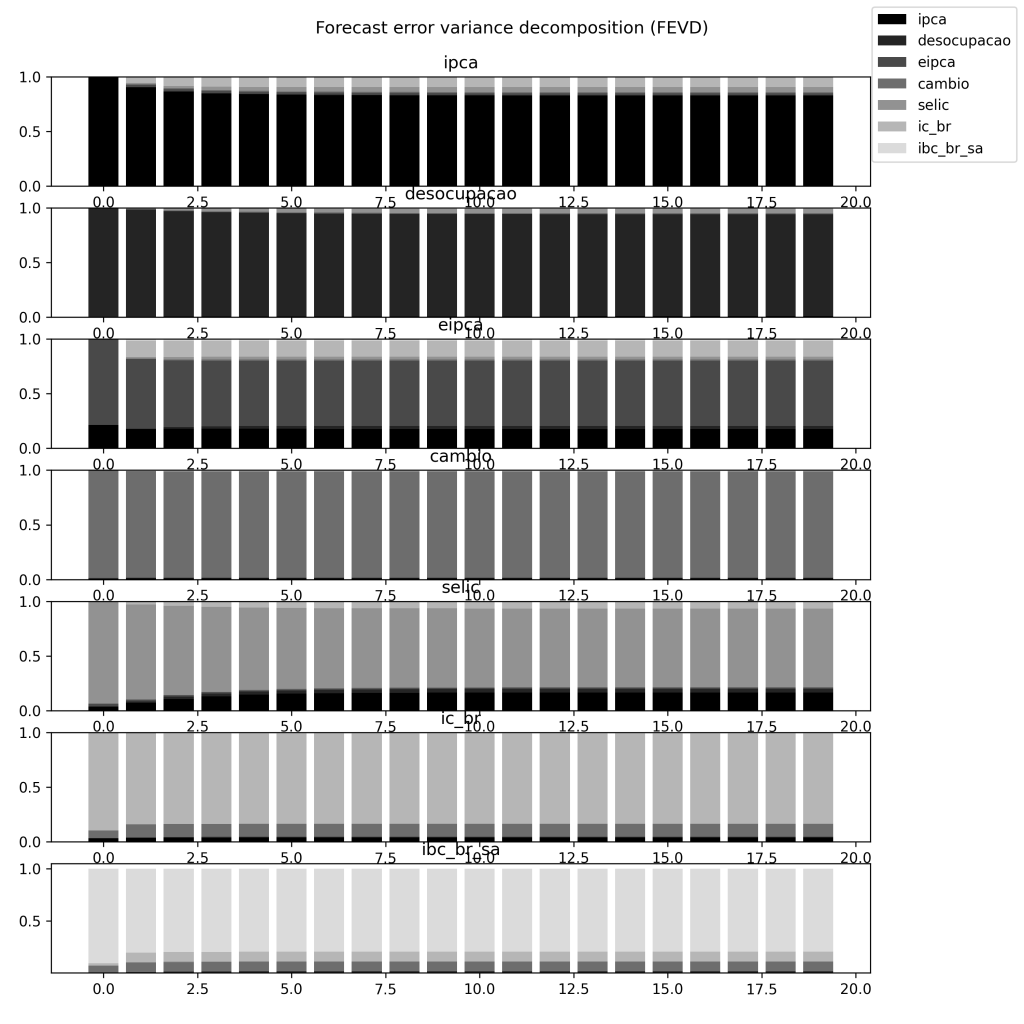
Decomposição de Variância
Outro tópico interessante para ver a relação entre duas ou mais variáveis é a decomposição de variância, isto é, o quanto da variância de uma variável do nosso conjunto é explicado pelas demais variáveis.
No Python, ela é implementada com o método fevd.
Código
FEVD for ipca
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
0 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
1 0.903966 0.003700 0.017149 0.009707 0.009465 0.054199 0.001813
2 0.863333 0.004399 0.019086 0.008744 0.021346 0.080053 0.003039
3 0.847148 0.004317 0.018911 0.008760 0.030242 0.087464 0.003158
4 0.839631 0.004243 0.018700 0.008824 0.036110 0.089343 0.003149
FEVD for desocupacao
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
0 0.003379 0.996621 0.000000 0.000000 0.000000 0.000000 0.000000
1 0.003782 0.980230 0.002477 0.002142 0.006942 0.004040 0.000388
2 0.006759 0.963558 0.002574 0.004687 0.015625 0.006279 0.000517
3 0.008130 0.953245 0.002422 0.006390 0.022645 0.006656 0.000513
4 0.008306 0.947144 0.002340 0.007166 0.027806 0.006735 0.000504
FEVD for eipca
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
0 0.215009 0.000064 0.784926 0.000000 0.000000 0.000000 0.000000
1 0.176290 0.003621 0.639874 0.000623 0.015225 0.149476 0.014892
2 0.179985 0.014351 0.609674 0.010931 0.020832 0.149754 0.014473
3 0.179252 0.021408 0.601714 0.012614 0.022742 0.147801 0.014469
4 0.178433 0.024747 0.598711 0.012726 0.023782 0.147173 0.014428
FEVD for cambio
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
0 0.009010 0.000220 0.005542 0.985228 0.000000 0.000000 0.000000
1 0.010102 0.000540 0.005651 0.974787 0.000152 0.000449 0.008319
2 0.010753 0.000674 0.005695 0.972016 0.000274 0.001880 0.008708
3 0.010934 0.000789 0.005693 0.971320 0.000387 0.002138 0.008739
4 0.011011 0.000856 0.005693 0.971021 0.000476 0.002205 0.008737
FEVD for selic
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
0 0.034932 0.004147 0.023867 0.002817 0.934237 0.000000 0.000000
1 0.070556 0.013394 0.014578 0.003231 0.868299 0.025365 0.004576
2 0.106640 0.020666 0.011519 0.003967 0.814335 0.038036 0.004837
3 0.131409 0.025174 0.010271 0.004288 0.778130 0.045950 0.004778
4 0.145813 0.028051 0.009742 0.004485 0.755580 0.051573 0.004756
FEVD for ic_br
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
0 0.030437 0.000819 0.002609 0.069271 0.000044 0.896820 0.000000
1 0.033382 0.004182 0.003702 0.117010 0.000072 0.834360 0.007292
2 0.035668 0.004922 0.003748 0.117523 0.000326 0.828988 0.008825
3 0.036285 0.005135 0.003848 0.117380 0.000788 0.827728 0.008836
4 0.036462 0.005256 0.003867 0.117282 0.001190 0.827112 0.008831
FEVD for ibc_br_sa
ipca desocupacao eipca cambio selic ic_br ibc_br_sa
0 0.000002 0.002245 0.001186 0.064615 0.001151 0.023767 0.907033
1 0.000015 0.006799 0.001030 0.089859 0.003434 0.091344 0.807519
2 0.000223 0.010766 0.001406 0.090004 0.005020 0.092061 0.800521
3 0.000460 0.012283 0.001407 0.089831 0.005720 0.091826 0.798472
4 0.000778 0.012831 0.001406 0.089733 0.005980 0.091762 0.797510
Observe que a maior parte da variância da inflação é explicada pela própria variável, seguida pelas expectativas. As demais variáveis do nosso modelo têm pouca ou nenhuma influência na variância da inflação.
SVAR
Para terminar, é preciso considerar um último ponto.
O modelo no VAR é o que a literatura chama de forma reduzida. Isto é, não estamos impondo nenhuma restrição ao mesmo, bem como estamos ignorando os efeitos contemporâneos que possam existir entre as variáveis.
Uma consequência natural dessa abordagem é que os parâmetros estimados devem ser vistos com bastante cuidado. Para contornar esse tipo de dificuldade, adota-se o conceito de VAR Estrutural (SVAR, no inglês), onde restrições obtidas da teoria podem ser incorporadas à modelagem, dando assim sentido aos parâmetros estimados.
De modo a ilustrar, considere que o modelo bivariado representado como
(8)
Reorganizando as variáveis em temos que
(9)
Onde
É assumido que os erros estruturais, representados por , são um ruído branco e que a matriz de coeficientes
corresponde a coeficientes estruturais, que irão diferir da forma reduzida representada pelo VAR se
, onde
é a matriz-identidade.
Nesses termos, temos um VAR estrutural ou SVAR, no inglês.^[Observe que é correlacionado com
, assim como
é correlacionado com
, o que inviabiliza na prática uma interpretação mais teórica dos parâmetros estimados na forma reduzida.]
Observe que se , voltamos para o mundo ilustrado pelo modelo bivariado. Isto é, estamos excluindo os efeitos contemporâneos entre as variáveis.
Se essa hipótese valer, a matriz de covariância será dada por . Isto é, os termos de erro não serão correlacionados contemporaneamente.
Naturalmente, não podemos observar a matriz de covariância, apenas estimá-la. Se, desse modo, os valores estimados fora da diagonal da matriz de covariância forem estatisticamente iguais a zero, teremos evidências de que a restrição será válida.
De forma a avançar, contudo, podemos generalizar o SVAR de modo a termos
Multiplicando @svargeral pela inversa de teremos
(10)
Não poderemos estimar esse modelo de forma direta, já que os resíduos serão estimativas de
, não sendo possível, de forma geral, obter estimativas únicas.
Esse é justamente o problema de identificação dos parâmetros. Um modelo SVAR, nesse contexto, pode ser utilizado para identificar choques e rastrear os mesmos empregando uma análise de impulso-resposta ou a decomposição de variância, vistas anteriormente. Para isso, precisaremos impor alguma restrição às matrizes A e/ou B. Dependendo da restrição imposta, poderemos ter três tipos de modelo SVAR, a saber:
1. A-model: é setado como
, onde o valor mínimo de restrições para identificação será
;
2. B-model: é setado como
, onde o valor mínimo de restrições para identificação também será
;
3. AB-model: as restrições podem ser colocadas em ambas as matrizes, onde o valor mínimo de restrições para identificação será .
Dependendo do tipo do SVAR, a estimação será similar à estimação de modelos de equações simultâneas com restrições sobre a matriz de variância-covarância dos termos de erro.
Para ilustrar, considere novamente o sistema
(11)
Como vimos acima, não poderemos estimar esse modelo de forma direta devido a problemas de identificação. Isso porque, a variável sofre um impacto de
de magnitude
ao mesmo tempo que dado este impacto,
sofrerá uma mudança de
devido a
. Isto impossibilitará a estimação de coeficientes não viesados e/ou consistentes.
Devemos, nesse contexto, ter alguma identificação entre e
, de modo a estimar esse sistema. Se, por exemplo, considerarmos por algum motivo que
, o problema colocado acima desaparece, permitindo que o sistema seja então estimado via mínimos quadrados ordinários.
Observe que ao fazer , na verdade, estamos dizendo que
não tem influência contemporânea sobre
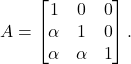
, implicando em uma matriz A do tipo triangular
(12)
Esse método é conhecido como decomposição de Cholesky, sendo um dos mais utilizados para gerar identificação entre variáveis.
Para ilustrar a operacionalização de um SVAR na prática, vamos considerar as variáveis desemprego diferenciado, selic diferenciado e ipca. O código abaixo seleciona as variáveis e estima um VAR(1).
Para ilustrar a operacionalização de um SVAR na prática, vamos considerar as variáveis desemprego diferenciado, selic diferenciado e ipca. O código abaixo seleciona as variáveis e estima um VAR(1).
Código
Podemos ver a matriz de covariância desse modelo na tabela abaixo.
Código
| ipca | desocupacao | selic | |
|---|---|---|---|
| ipca | 0.151468 | -0.005107 | 0.064903 |
| desocupacao | -0.005107 | 0.099911 | -0.030318 |
| selic | 0.064903 | -0.030318 | 0.145280 |
A matriz de covariância mostra que os valores fora da diagonal são diferentes de zero, implicando que . Dessa forma, a especificação reduzida pode não ser a mais correta.
Assim, de modo a incluir efeitos contemporâneos, devemos impor uma diferente estrutura para a matriz . Para isso, vamos supor que o desemprego não é afetado por nenhuma das outras variáveis contemporâneamente, porém, que a inflação é afetada pelo desemprego contemporâneamente.
Finalmente, assumimos que a taxa de juros é determinada somente por defasagens das outras variáveis. Esta última hipótese também pode ser interpretada como o Banco Central não sendo capaz de observar o nível de desemprego e preços no mesmo instante que irá determinar a taxa de juros.
Assim, nossa matriz deveria ser algo como
(13)
Abaixo estimamos o modelo estrutural e obtemos os IRFs impondo a restrição acima.
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas

![Rendered by QuickLaTeX.com \[z_{t} = \phi_{0} + \sum_{i=1}^{p} \phi_{i} z_{t-i} + \alpha_{t}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-d8bf85a158f05646ab8f74d6036a13b5_l3.png)
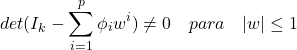

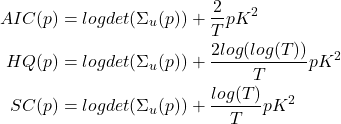
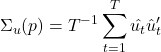

![Rendered by QuickLaTeX.com \[A\mathbf{z}_t = A^{w}_0 + \sum_{i=1}^p A^{w}_i \mathbf{z}_{t-p} + B\varepsilon_t\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-6889dd4f8ab42719a6b1d73700f1efd6_l3.png)