Pré-processamento de dados: lidando com valores extremos e valores ausentes

Vazamento de dados (data leakage)

Vazamento de dados, do inglês data leakage, é um termo utilizado em ciência de dados para se referir a quando acontece, em um processo de validação de um modelo (simulação), a exposição de informações que não estariam disponíveis para o modelo em ambiente de produção (fora da simulação). Em outras palavras, o modelo é estimado/treinado com informações que ele não teria acesso na prática, ou seja, com dados não vistos/futuros. O termo pode ser confuso (em geral, as pessoas pensam em vazamento de emails, dados financeiros, etc.), então um exemplo talvez clarifique a ideia.

Por exemplo: você quer prever as vendas mensais usando a tendência e outras métricas como variáveis explicativas. Você calcula a tendência temporal das vendas usando o conjunto de dados completo, então separa-o em amostras de treino e teste e usa a amostra de treino para estimar/treinar um modelo. Percebeu o problema? A variável tendência, na amostra de treino, possui informações sobre o futuro (da amostra de teste) que na prática não estarão disponíveis no momento de previsão “fora da amostra”.

Quando acontece vazamento de dados, as estimativas do modelo não são confiáveis e é provável que as previsões não sejam acuradas. Dessa forma, é extremamente importante tomar todas as precauções necessárias para evitar, durante o treinamento de um modelo, que aconteça vazamento de dados. Essa é uma tarefa difícil e complexa e que até mesmo as principais referências na área de ciência de dados acabam cometendo “deslizes” vez ou outra (veja o caso “famoso” de Andrew Ng em Rajpurkar et al. (2017)).

Tudo isso para dizer que a etapa de pré-processamento de dados é bastante suscetível a vazamento de dados. A seguir, vamos abordar alguns casos de pré-processamento de dados e maneiras de evitar o vazamento de dados.

Valores extremos (outliers)

Modelos estatísticos, econométricos e de aprendizado de máquina são, em geral, sensíveis à distribuição e intervalo dos dados. Eventos raros, valores extremos, outliers, etc., podem gerar estimativas e previsões viesadas por influência desses valores, além de dificultar ou impossibilitar a convergência de algoritmos.

Por exemplo: imagine que você tenha um modelo que prevê a média de uma variável alvo qualquer. Em um determinado dia acontece um evento raro (i.e., pandemia) e sua variável alvo é afetada com o registro de um valor extremo. Dessa forma, as próximas previsões do seu modelo serão deslocadas para uma faixa de valores na direção do valor extremo, pois a média é uma estatística sensível a esses grandes números, mesmo que o evento raro tenha acontecido somente uma vez e tudo tenha voltado ao “normal” após o evento.

Existem pelo menos três abordagens para lidar com valores extremos em modelos preditivos:

• Remoção: é o processo de identificar, baseado em alguma regra, os valores extremos na distribuição de dados e remover, seja a variável ou apenas a observação.
• Substituição: é o processo de identificar, baseado em alguma regra, os valores extremos na distribuição de dados e substituir a observação por outro valor usando alguma estatística dos dados, ou método de proximidade, ou valor discricionário, ou outros.
• Dummy: é o processo de identificar, baseado em alguma regra, os valores extremos na distribuição de dados e adicionar, no modelo preditivo, uma dummy que assume valor 1 para a observação extrema e 0 caso contrário.

Não existe abordagem geral para todos os cenários e casos de uso. A recomendação é analisar o valor extremo, investigar a fonte do mesmo e, então, decidir o que fazer (se algo deve ser feito) com o mesmo em um modelo preditivo.

Como evitar vazamento de dados: sempre separe as amostras de treino e teste primeiro e, somente após isso, aplique os pré-processamentos que julgar necessários individualmente nas amostras.

Valores ausentes (missing data)

Valores ausentes são dados que não estão preenchidos em uma dada observação de uma variável, geralmente codificados como NA, NaN ou outras codificações. É um “buraco” muito comum em conjuntos de dados reais que pode ser oriundo de diversas causas (i.e., feriado, não obrigatoriedade de preenchimento, problemas de infraestrutura técnica, etc.). Para grande parte dos modelos preditivos, os valores ausentes são um problema que o cientista/analista precisa lidar, pois os estimadores supõem que todos os valores de um vetor sejam numéricos.

Existem pelo menos duas abordagens para lidar com valores ausentes em modelos preditivos:

• Exclusão: é o processo de identificar, baseado em alguma codificação, os valores ausentes na distribuição de dados, avaliar a proporção de valores ausentes em relação ao total de linhas e decidir entre a exclusão da variável (coluna) ou da observação (linha).
• Imputação: é o processo de identificar, baseado em alguma codificação, os valores ausentes na distribuição de dados e substituir por alguma estatística, valor discricionário, valor próximo, método de proximidade ou outros.

Não existe abordagem geral para todos os cenários e casos de uso. A recomendação é analisar os valores ausentes, sua proporção, investigar a fonte do mesmo e, então, decidir o que fazer (se algo deve ser feito) com o mesmo em um modelo preditivo.

Como evitar vazamento de dados: sempre separe as amostras de treino e teste primeiro e, somente após isso, aplique os pré-processamentos que julgar necessários individualmente nas amostras.

Exemplo prático com dados econômicos

Agora vamos demonstrar como aplicar alguns pré-processamentos em um conjunto de dados econômicos. Uma tabela interessante de se trabalhar é a Pesquisa Nacional por Amostra de Domicílios Contínua (PNAD-C) do IBGE, que disponibiliza os microdados da pesquisa trazendo informações sobre renda, educação e outros. Por ser uma pesquisa, com pessoas/domicílios, a PNAD-C costuma ter diversos valores ausentes e extremos, o que é excelente para praticar as abordagens.

Abaixo apresentamos as primeiras linhas da tabela da PNAD-C (ano 2022, trimestre 4):

# A tibble: 6 × 421
    Ano Trimestre    UF Capital RM_RIDE      UPA Estrato V1008 V1014 V1016 V1022
  <dbl>     <dbl> <dbl>   <dbl>   <dbl>    <dbl>   <dbl> <chr> <chr> <dbl> <dbl>
1  2022         4    11      11      NA   1.10e8 1110011 01    10        1     1
2  2022         4    11      11      NA   1.10e8 1110011 01    10        1     1
3  2022         4    11      11      NA   1.10e8 1110011 02    10        1     1
4  2022         4    11      11      NA   1.10e8 1110011 03    10        1     1
5  2022         4    11      11      NA   1.10e8 1110011 03    10        1     1
6  2022         4    11      11      NA   1.10e8 1110011 04    10        1     1
# ℹ 410 more variables: V1023 <dbl>, V1027 <dbl>, V1028 <dbl>, V1029 <dbl>,
#   V1033 <dbl>, posest <dbl>, posest_sxi <dbl>, V2001 <dbl>, V2003 <chr>,
#   V2005 <chr>, V2007 <dbl>, V2008 <chr>, V20081 <chr>, V20082 <dbl>,
#   V2009 <dbl>, V2010 <dbl>, V3001 <dbl>, V3002 <dbl>, V3002A <dbl>,
#   V3003 <lgl>, V3003A <chr>, V3004 <lgl>, V3005 <lgl>, V3005A <dbl>,
#   V3006 <chr>, V3006A <lgl>, V3007 <dbl>, V3008 <dbl>, V3009 <lgl>,
#   V3009A <chr>, V3010 <dbl>, V3011 <lgl>, V3011A <dbl>, V3012 <dbl>, …

    Ano  Trimestre  UF  ...    V1028199  V1028200   ID_DOMICILIO
0  2022          4  11  ...  298.760783       0.0  1100000160110
1  2022          4  11  ...  298.760783       0.0  1100000160110
2  2022          4  11  ...  158.839984       0.0  1100000160210
3  2022          4  11  ...  281.073395       0.0  1100000160310
4  2022          4  11  ...  281.073395       0.0  1100000160310

[5 rows x 421 columns]

Agora vamos separar os dados dessa tabela, um corte transversal, em amostras de treino e teste por amostragem aleatória simples, visando evitar o vazamento de dados durante (não demonstraremos os procedimentos de modelagem preditiva aqui, mas seria isso que deveria ser feito para não contaminar a amostra de treinamento). Abaixo apresentamos as linhas finais da amostra de treino e as linhas iniciais da amostra de teste:

# A tibble: 6 × 421
    Ano Trimestre    UF Capital RM_RIDE      UPA Estrato V1008 V1014 V1016 V1022
  <dbl>     <dbl> <dbl>   <dbl>   <dbl>    <dbl>   <dbl> <chr> <chr> <dbl> <dbl>
1  2022         4    53      53      NA   5.30e8 5310111 09    10        4     1
2  2022         4    53      53      NA   5.30e8 5310111 10    10        4     1
3  2022         4    53      53      NA   5.30e8 5310111 11    10        4     1
4  2022         4    53      53      NA   5.30e8 5310111 11    10        4     1
5  2022         4    53      53      NA   5.30e8 5310111 13    10        4     1
6  2022         4    53      53      NA   5.30e8 5310111 14    10        4     1
# ℹ 410 more variables: V1023 <dbl>, V1027 <dbl>, V1028 <dbl>, V1029 <dbl>,
#   V1033 <dbl>, posest <dbl>, posest_sxi <dbl>, V2001 <dbl>, V2003 <chr>,
#   V2005 <chr>, V2007 <dbl>, V2008 <chr>, V20081 <chr>, V20082 <dbl>,
#   V2009 <dbl>, V2010 <dbl>, V3001 <dbl>, V3002 <dbl>, V3002A <dbl>,
#   V3003 <lgl>, V3003A <chr>, V3004 <lgl>, V3005 <lgl>, V3005A <dbl>,
#   V3006 <chr>, V3006A <lgl>, V3007 <dbl>, V3008 <dbl>, V3009 <lgl>,
#   V3009A <chr>, V3010 <dbl>, V3011 <lgl>, V3011A <dbl>, V3012 <dbl>, …

# A tibble: 6 × 421
    Ano Trimestre    UF Capital RM_RIDE      UPA Estrato V1008 V1014 V1016 V1022
  <dbl>     <dbl> <dbl>   <dbl>   <dbl>    <dbl>   <dbl> <chr> <chr> <dbl> <dbl>
1  2022         4    11      11      NA   1.10e8 1110011 02    10        1     1
2  2022         4    11      11      NA   1.10e8 1110011 03    10        1     1
3  2022         4    11      11      NA   1.10e8 1110011 04    10        1     1
4  2022         4    11      11      NA   1.10e8 1110011 05    10        1     1
5  2022         4    11      11      NA   1.10e8 1110011 10    10        1     1
6  2022         4    11      11      NA   1.10e8 1110011 02    10        4     1
# ℹ 410 more variables: V1023 <dbl>, V1027 <dbl>, V1028 <dbl>, V1029 <dbl>,
#   V1033 <dbl>, posest <dbl>, posest_sxi <dbl>, V2001 <dbl>, V2003 <chr>,
#   V2005 <chr>, V2007 <dbl>, V2008 <chr>, V20081 <chr>, V20082 <dbl>,
#   V2009 <dbl>, V2010 <dbl>, V3001 <dbl>, V3002 <dbl>, V3002A <dbl>,
#   V3003 <lgl>, V3003A <chr>, V3004 <lgl>, V3005 <lgl>, V3005A <dbl>,
#   V3006 <chr>, V3006A <lgl>, V3007 <dbl>, V3008 <dbl>, V3009 <lgl>,
#   V3009A <chr>, V3010 <dbl>, V3011 <lgl>, V3011A <dbl>, V3012 <dbl>, …

         Ano  Trimestre  UF  ...    V1028199    V1028200   ID_DOMICILIO
75545   2022          4  21  ...    0.000000  223.698358  2100318690710
132851  2022          4  23  ...    0.000000  152.367255  2302107720910
169727  2022          4  26  ...  270.943490    0.000000  2601321061010
292463  2022          4  33  ...  245.477555    0.000000  3301556250710
381148  2022          4  42  ...  467.428530    0.000000  4200233090210

[5 rows x 421 columns]

         Ano  Trimestre  UF  ...     V1028199     V1028200   ID_DOMICILIO
234236  2022          4  31  ...     0.000000   106.282648  3100936730310
22234   2022          4  13  ...  1492.279455     0.000000  1300294160510
100414  2022          4  22  ...   214.927316     0.000000  2200072031010
417074  2022          4  43  ...   701.293670  1053.547610  4301070841010
13711   2022          4  12  ...    94.998281    96.767922  1200079700510

[5 rows x 421 columns]

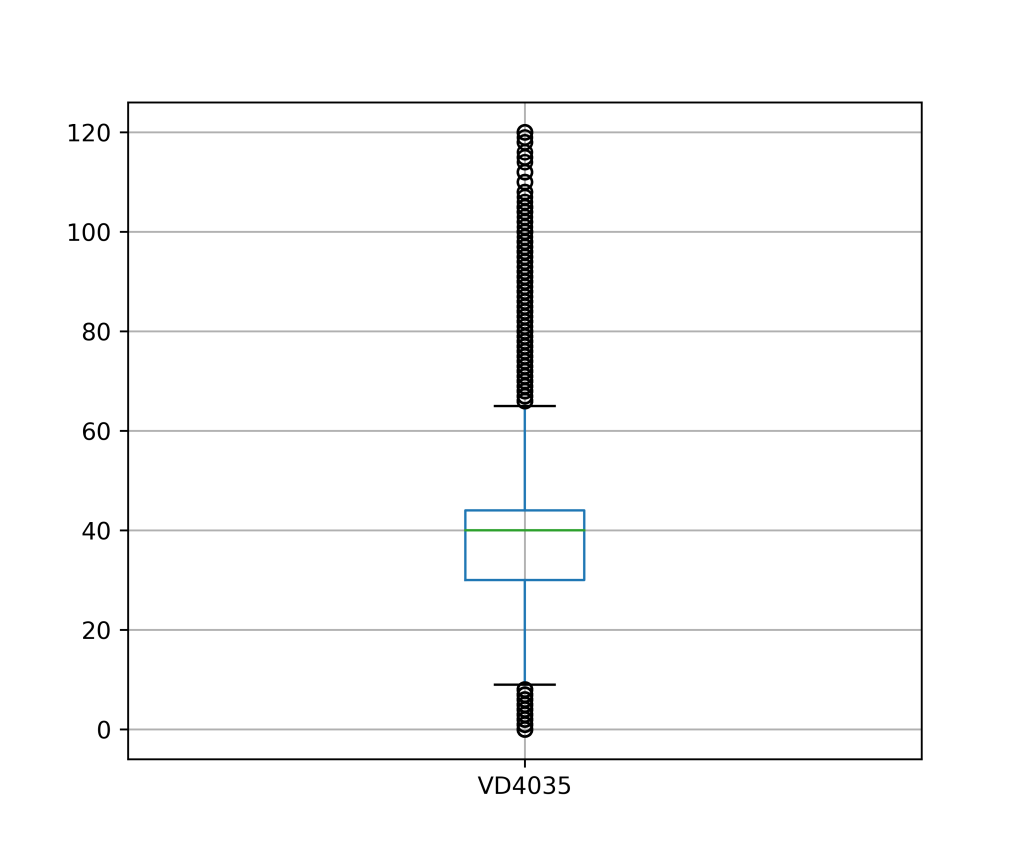
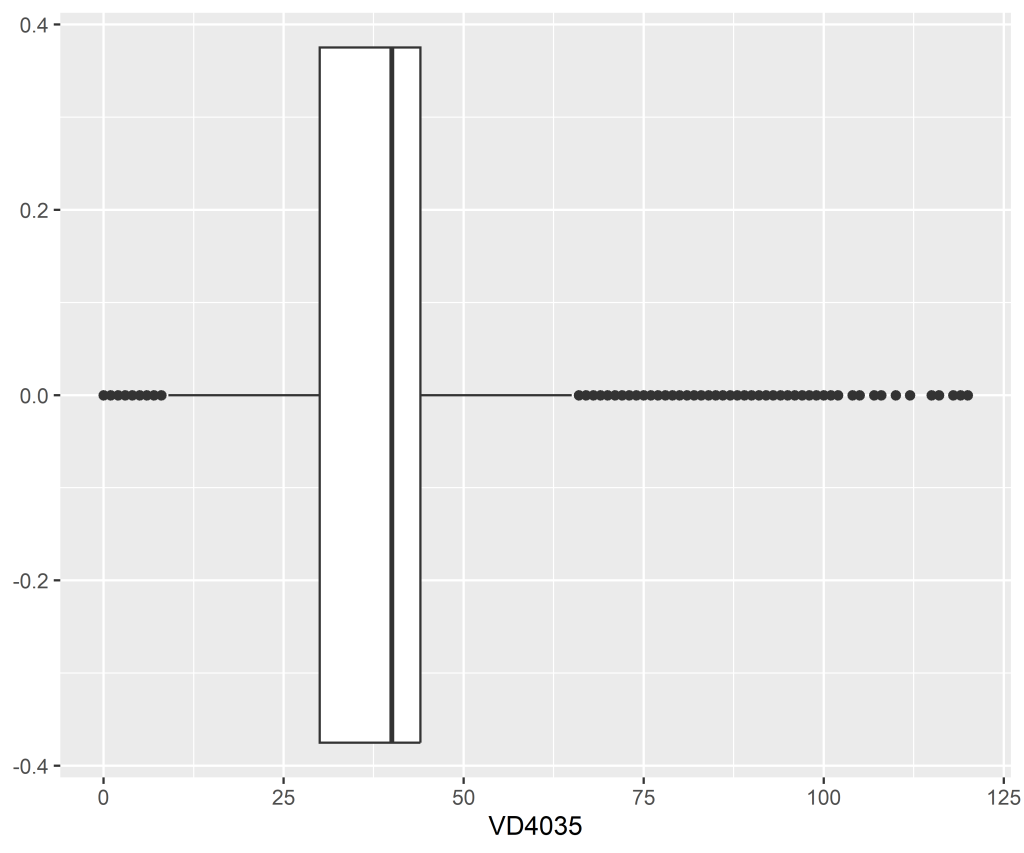
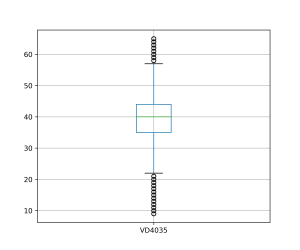
Com os dados preparados, vamos verificar se a amostra de treino possui valores extremos, tomando como exemplo a variável quantitativa “Horas efetivamente trabalhadas na semana de referência em todos os trabalhos para pessoas de 14 anos ou mais de idade” (VD4035). Isso pode ser feito de diversas formas: uma das maneiras mais simples é através de ferramentas de visualização de dados, como um boxplot.

Como pode ser visto, essa variável é cheia de valores extremos (desigualdade social?). Uma vez que esses valores tenham sido identificados, você pode querer aplicar um pré-processamento. Vamos supor que para o objetivo do estudo faça sentido remover essas observações (linhas). Abaixo plotamos o boxplot novamente após este pré-processamento na tabela de treino (utilizando a regra do IQR, conforme Hyndman e Athanasopoulos (2021)), sendo que o mesmo deve ser feito na tabela de teste:

Nota-se uma grande redução do intervalo da distribuição da variável, mas com uma “nova” distribuição podem haver novos valores extremos para essa distribuição, mesmo que ela seja mais “comportada” em relação a distribuição anterior.

# A tibble: 1 × 1
  prop_na
    <dbl>
1   0.569

0.5682223610019632

     VD4035      
 Min.   :  0.00  
 1st Qu.: 30.00  
 Median : 40.00  
 Mean   : 37.82  
 3rd Qu.: 44.00  
 Max.   :120.00  
 NA's   :190488  

     VD4035      
 Min.   :  0.00  
 1st Qu.: 37.82  
 Median : 37.82  
 Mean   : 37.82  
 3rd Qu.: 40.00  
 Max.   :120.00  

count    144500.000000
mean         37.855751
std          13.917319
min           0.000000
25%          30.000000
50%          40.000000
75%          44.000000
max         120.000000
Name: VD4035, dtype: float64

count    334663.000000
mean         37.855751
std           9.145023
min           0.000000
25%          37.855751
50%          37.855751
75%          40.000000
max         120.000000
Name: VD4035, dtype: float64