Quanto vale seu carro? Uma aplicação de Árvores de Decisão

Neste artigo, vamos descrever métodos baseados em árvores, que servem tanto para resolver problemas de regressão quanto de classificação. Eles envolvem estratificar e segmentar o espaço de previsão em um número de regiões simples. Assim, de modo a fazer a previsão de uma observação qualquer, nós usamos a média ou a moda do conjunto de treino da região a que ela pertence.¹

O nome desse tipo de método vem justamente da ideia de que as regras de decisão utilizadas para segmentar o espaço de previsão podem ser sumarizadas em uma árvore.

Métodos baseados em árvores são simples e úteis para interpretação.

Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.

Árvores de Regressão

Vamos motivar o uso de árvores de regressão com um exemplo simples. Suponha que estamos interessados em prever o salário de jogadores de baseball a partir do número de anos que ele joga nas ligas principais e no número de acertos do ano anterior. Considere o dataset Hitters do pacote ISLP:

	Hits	Salary
count	322.000000	263.000000
mean	101.024845	535.925882
std	46.454741	451.118681
min	1.000000	67.500000
25%	64.000000	190.000000
50%	96.000000	425.000000
75%	137.000000	750.000000
max	238.000000	2460.000000

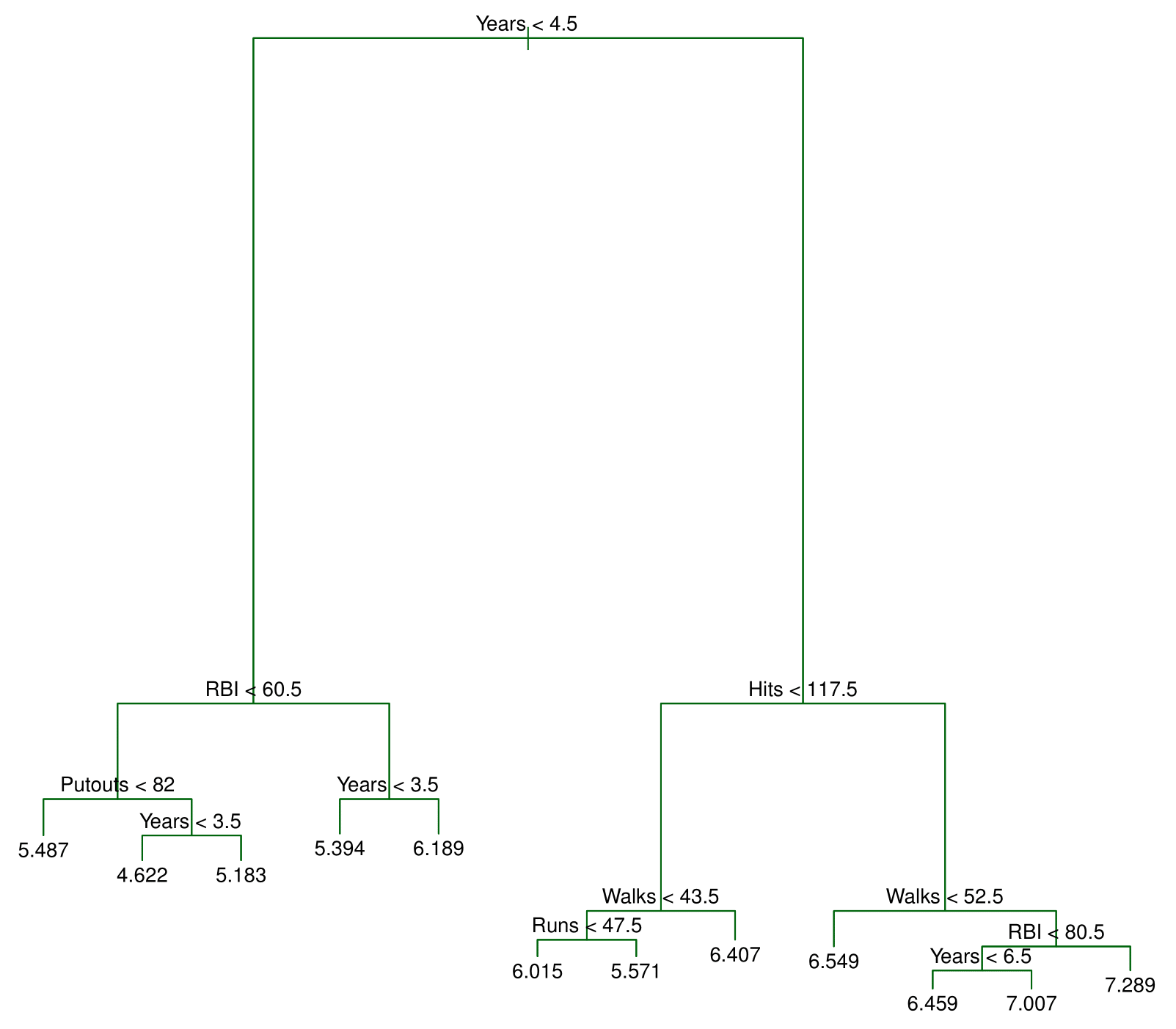
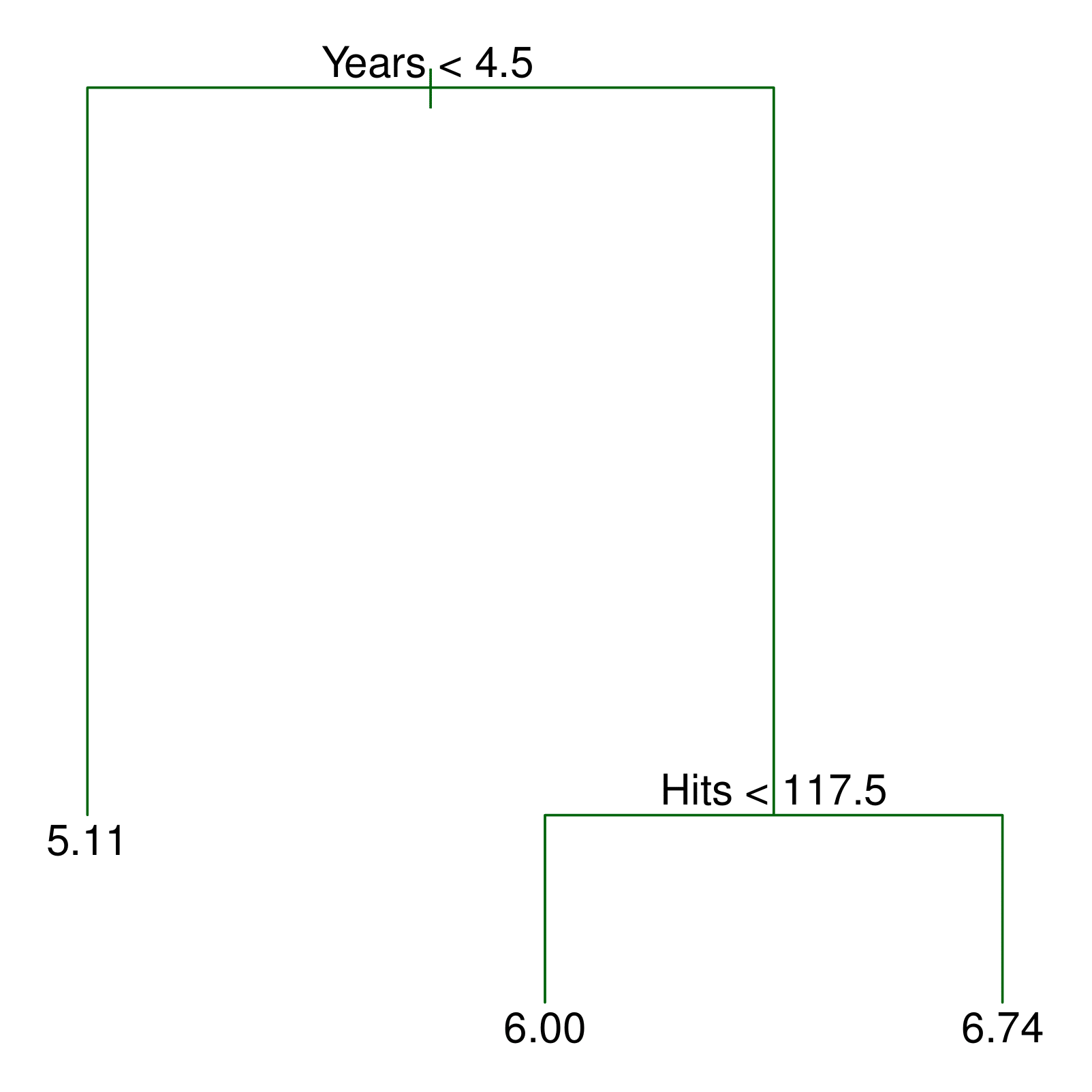
A figura 1 ilustra uma árvore de decisão para prever o log do salário de um jogador de baseball, baseado no número de anos que ele joga nas ligas principais e no número de acertos que ele fez no ano anterior. Em um determinado nó interno, o rótulo para o lado esquerdo (na forma $X_j < t_k$ ) indica quanto o é o salário em log esperado para menos de 4,5 anos. Para o lado direito, na forma $X_j \geq t_k$ , quanto é o salário para 4,5 ou mais anos.

O salário previsto para esses jogadores será dado pelo valor médio para os jogadores contidos no dataset, considerando o número de anos menor do que 4,5. Para esses jogadores, o salário médio em log será de 5.107, isto é, $e^{5.107}$ que fica em US$ 165.174.

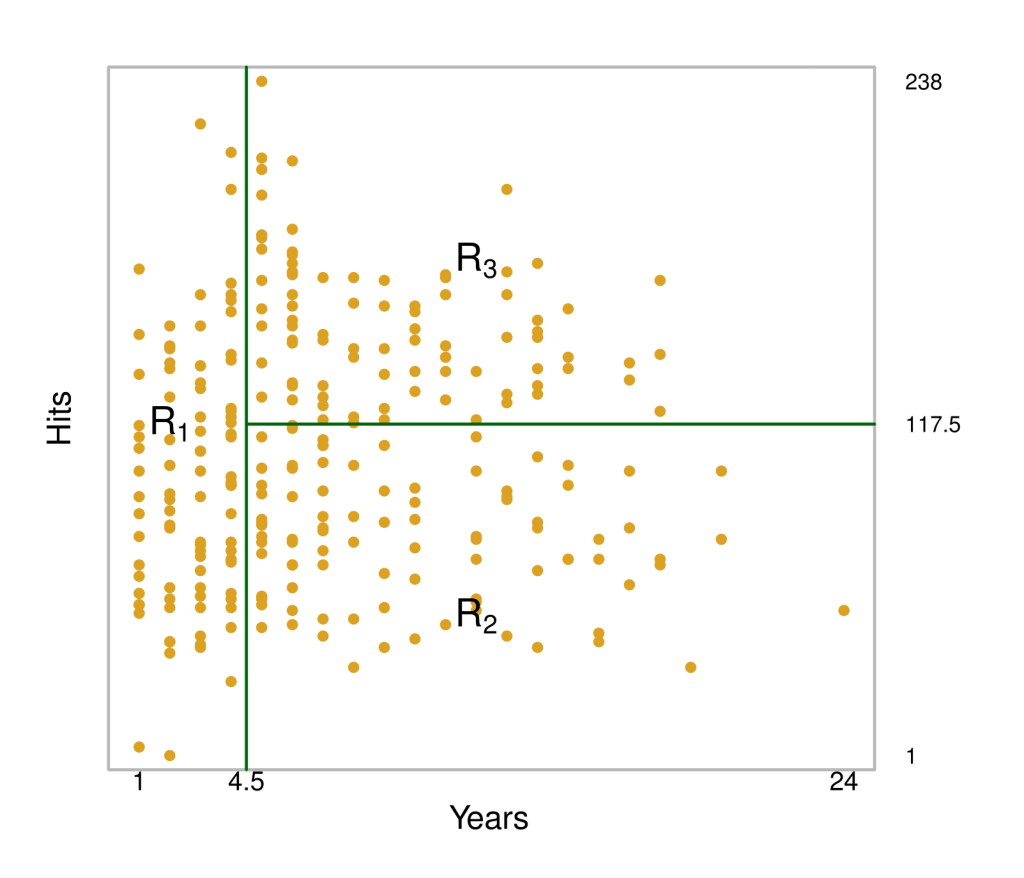
Já jogadores com mais de 4,5 anos estão organizados do lado direito e divididos pelo número de acertos. Assim, nossa árvore está segmentando os jogadores em três regiões: (1) os que jogaram menos de 4,5 anos; (2) aqueles que jogaram mais (ou igual a) do que 4,5 anos e que acertaram menos do que 117,5 no ano passado; (3) jogadores que jogaram mais do que 4,5 anos e que acertaram mais do que 117,5.

Essas regiões podem ser escritas como

$R_1 &= {X | Years < 4.5} \nonumber \\$

$R_2 &= {X | Years \geq 4.5, Hits < 117.5} \nonumber \\$

$R_3 &= {X | Years \geq 4.5, Hits \geq 117.5} \nonumber$

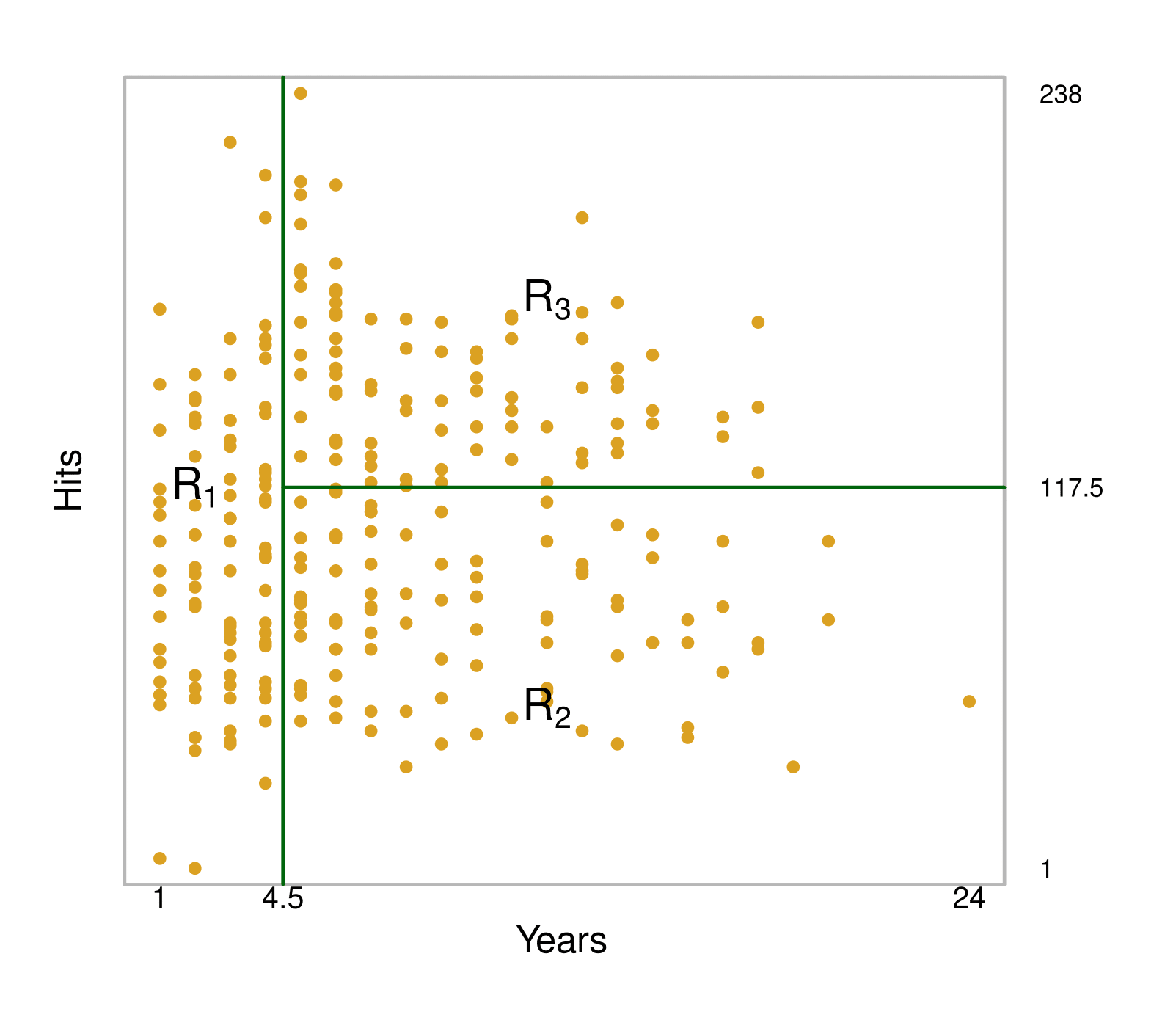
Os pontos ao longo da árvore onde os espaços de previsão são divididos são chamados de nós internos.

Assim, nós podemos interpretar a árvore de regressão da figura 1 da seguinte forma: a variável Years é o fator mais importante para determinar o salário dos jogadores, de modo que jogadores com menos experiência ganham salários menores do que jogadores com mais experiência. Dado um jogador com menos experiência, o número de acertos possui menos importância para determinar o seu salário. Já jogadores com mais experiência têm seus salários afetados pelo número de acertos feitos no ano anterior.

Vamos discutir agora o processo de construção de uma árvore de regressão. Há dois passos:

1. Nós dividimos o espaço de previsão, isto é, o conjunto de possíveis valores para $X_1, X_2,..., X_p$ em $J$ regiões distintas e não sobrepostas, $R_1, R_2,...,R_j$ .

2. Para cada observação que fica dentro da região $R_j$ , nós fazemos a mesma previsão, que é simplesmente a média dos valores de resposta para as observações de treinamento em $R_j$ .

Supondo duas regiões, $R_1$ e $R_2$ , e que a resposta média das observações de treino na primeira região seja 10 enquanto a resposta média das observações de treino na segunda região seja 20. Então, para uma dada observação $X = x$ , se $X \in R_1$ , nós prevemos um valor de 10, se $x \in R_2$ , nós prevemos um valor de 20.

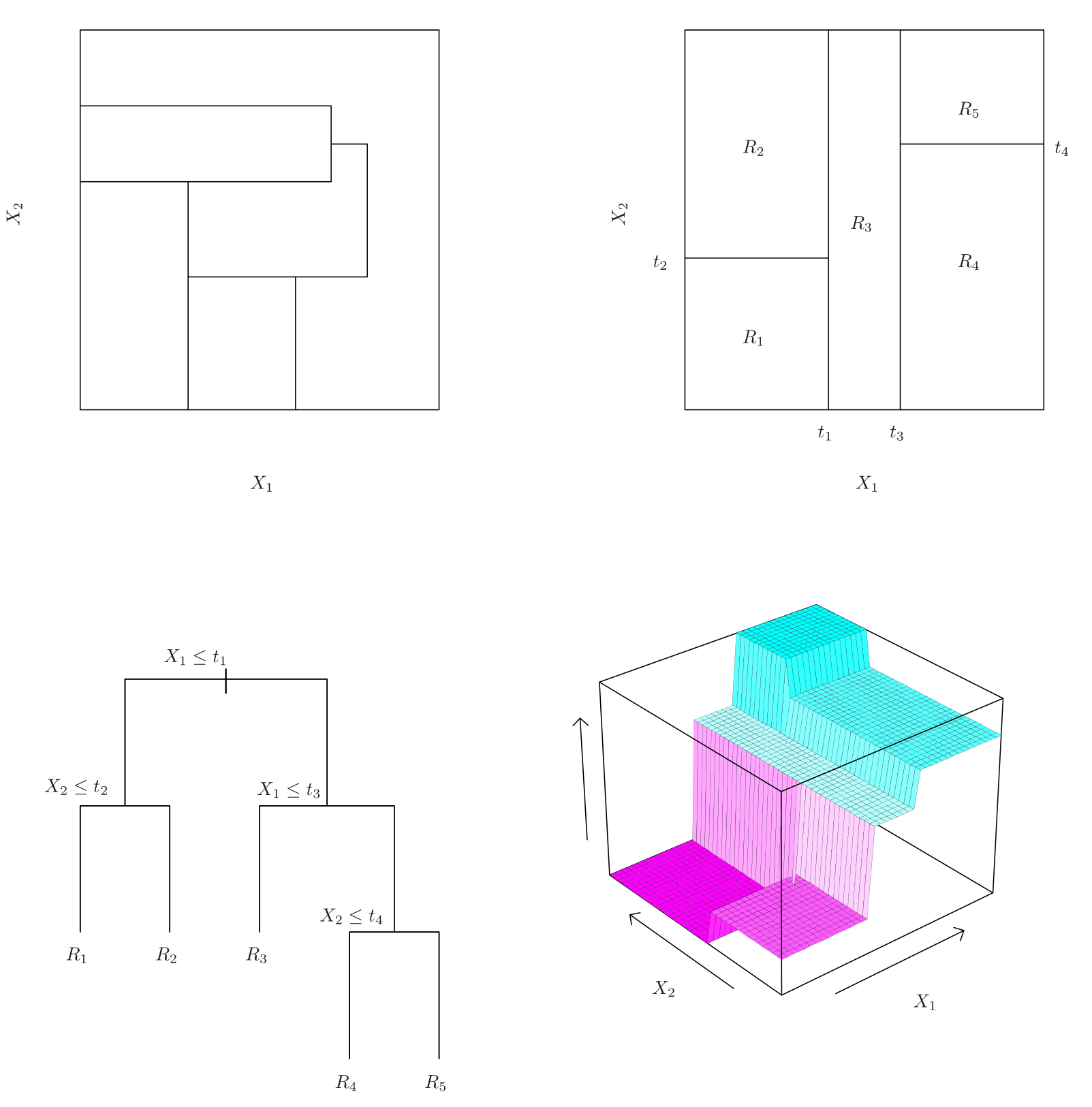
Como nós construímos as regiões $R_1,...,R_j$ ? Na teoria, as regiões podem ter qualquer formato. Entretanto, nós escolhemos dividir o espaço de preditores em retângulos de alta dimensão, ou simplesmente boxes, de modo a simplificar e facilitar a interpretação dos resultados do modelo preditivo. O objetivo é encontrar boxes $R_1,...,R_j$ que minimize

$\sum_{j=1}^{J} \sum_{i \in R_j}^{} (y_i - \hat{y}_{R_j})^2 \label{rss},$

onde $\hat{y}_{R_j}$ é a resposta média para as observações de treino contidas no box $j$ .

Infelizmente, é computacionalmente inviável considerar toda possível partição do espaço em $J$ boxes. Por essa razão, nós tomamos um top-down, uma abordagem ambiciosa chamada de divisão binária recursiva.

A abordagem é chamada de top-down, porque ela se inicia no topo da árvore e vai dividindo o espaço preditor. Cada divisão é indicada via dois novos ramos até o final da árvore. É ambiciosa porque a cada passo do processo de construção da árvore, a melhor divisão é feita em um passo particular, ao invés de olhar à frente e escolher a divisão que irá levar a uma melhor árvore em um passo futuro.

De modo a performar a divisão binária recursiva, nós primeiro selecionamos o preditor $X_j$ e o ponto de corte $s$ de modo a dividir o espaço preditor em regiões { $X|X_j < s$ } e { $X|X_j \geq s$ } que irão minimizar Equação 1.

Isto é, para cada $j$ e $s$ , nós definimos o par

$R_1(j,s) = {X|X_j < s} \text{e} R_2(j,s) = {X|X_j \geq s},$

e escolhemos o par que minimiza a equação

$\sum_{i:x_i \in R_1(j,s)}^{} (y_i - \hat{y}_{R_1})^2 + \sum_{i:x_i \in R_2(j,s)}^{} (y_i - \hat{y}_{R_2})^2,$

onde $\hat{y}_{R_1}$ é a resposta média para as observações de treino contidas em $R_1(y,s)$ .

O processo continua até que chega-se a um critério de parada. Nós devemos continuar até que não tenhamos região com mais de cinco observações.

Uma vez que as regiões $R_1,...,R_j$ são criadas, nós prevemos a resposta para um dado conjunto de observações de teste utilizando a média das observações de treino na região ao qual a observação de teste pertence.

O processo descrito acima pode produzir boas previsões sobre o conjunto de treino, mas é provável que gere um overfit (sobreajuste) sobre os dados, levando a uma performance fraca no conjunto de teste. Isso ocorre porque a árvore resultante pode ser muito complexa.

Uma árvore menor com poucas divisões pode levar a menor variância e melhor interpretação ao custo de um pequeno viés. Uma alternativa ao processo descrito acima é o de construir a árvore apenas até o ponto em que a equação Equação 1 cai devido a cada divisão exceder algum limite. Essa estratégia irá resultar em árvores menores.

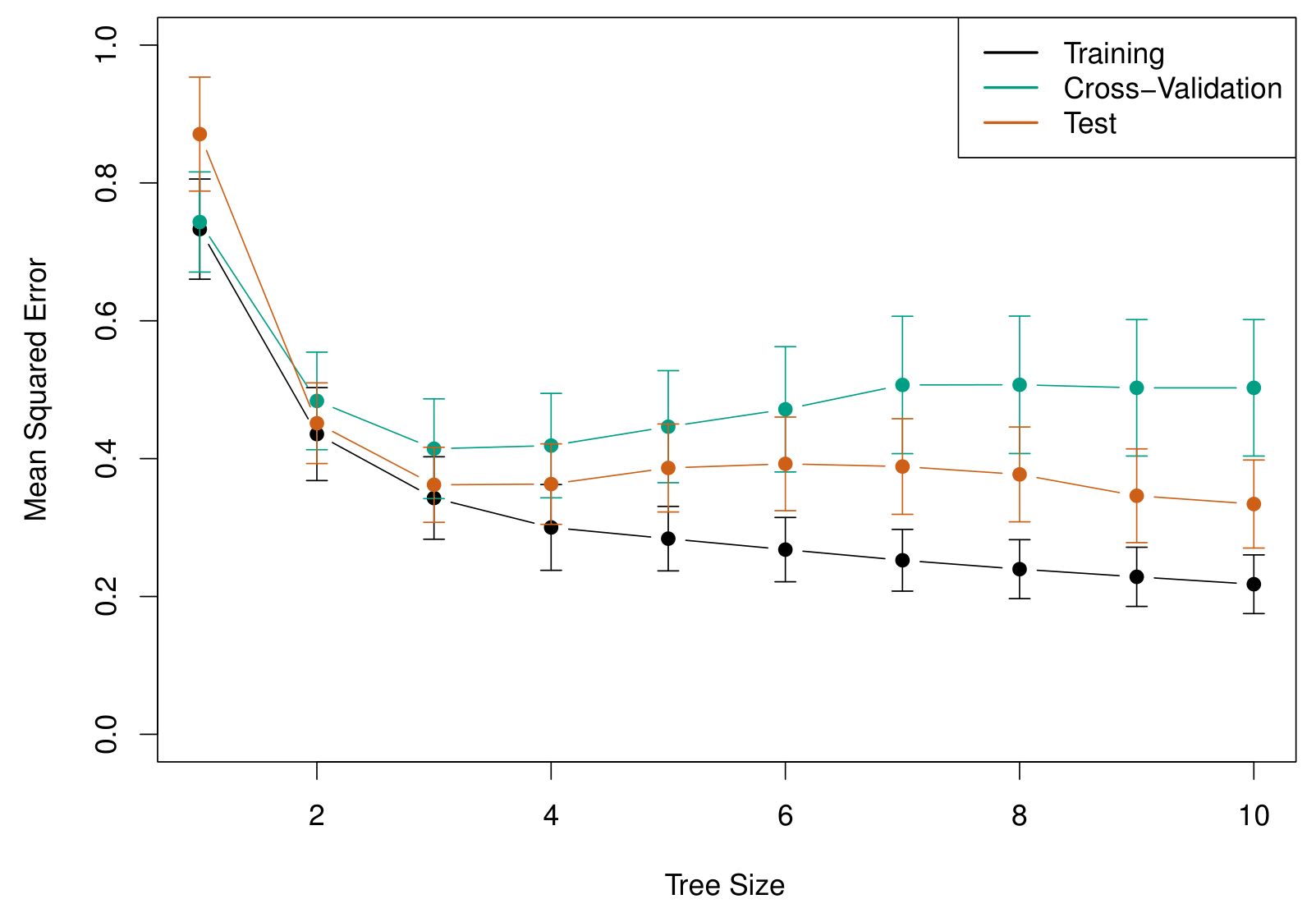
Assim, uma estratégia melhor é construir uma árvore grande $T_0$ e então ir podando a mesma, de modo a obter uma sub-árvore. Intuitivamente, nosso objetivo é selecionar uma sub-árvore que leva a uma menor taxa de erro no conjunto de testes. Nós precisaremos então de um meio para selecionar um pequeno conjunto de sub-árvores para avaliação.

Cost complexity pruning (poda por custo-complexidade) nos dá um meio de fazer isso. Ao invés de considerar cada possível sub-árvore, nós consideramos uma sequência de árvores indexadas por um parâmetro $\alpha$ .

Cada valor de $\alpha$ corresponde a uma sub-árvore $T \subset T_0$ de modo que

$\sum_{m=1}^{|T|} \sum_{x_i \in R_m} (y_i - \hat{y}_{R_m})^ + \alpha T \label{rss2}$

será o menor possível. Aqui, $|T|$ indica o número de nós terminais da árvore $T$ , $R_m$ é o número de subconjuntos do espaço preditor e $\hat{y}_{R_m}$ será a resposta predita associada a $R_m$ . O parâmetro $\alpha$ irá controlar o trade-off entre a complexidade das sub-árvores e o seu ajuste ao conjunto de treino.² À medida que $\alpha$ aumenta, haverá um preço a se pagar para ter uma árvore com muitos nós terminais, de modo que a soma dada por Equação 2 tenderá a ser minimizada para um número menor de sub-árvores. Isto é, à medida que $\alpha$ aumenta, os ramos (nós internos) da árvore serão podados.

Árvores de Classificação

Uma árvore de classificação é similar a uma árvore de regressão, com a diferença que a utilizamos para prever uma resposta qualitativa ao invés de uma resposta quantitativa.

Como vimos, na árvore de regressão, a resposta prevista para uma observação é dada pela resposta média das observações de treino que pertencem ao mesmo nó terminal.

Já na árvore de classificação, nós prevemos que cada observação pertence à classe mais comum das observações de treino da região a que elas pertencem.

Na interpretação dos resultados de uma árvore de classificação, geralmente estamos interessados não apenas na previsão da classe correspondente a uma região de nó terminal específica, mas também nas proporções de classe entre as observações de treinamento que se enquadram nesta região.

O processo de construção de uma árvore de classificação é bastante similar ao de uma árvore de regressão. Assim como lá, também usamos a divisão binária recursiva para construir uma árvore de classificação. Entretanto, aqui não podemos usar como critério a minimização da equação Equação 1.

Uma alternativa é a taxa de erro de classificação. Dado que nosso objetivo é atribuir uma observação em uma dada região à classe mais comum das observações de treino daquela região, a taxa de erro de classificação será a fração das observações de treino naquela região que não pertencem à classe mais comum:

$E = 1 - \max_{k} (\hat{p}_{mk}).$

Onde $\hat{p}_{mk}$ representa a proporção de observações de treino na região $m$ que é da classe $k$ .

A taxa de erro de classificação, contudo, não é suficientemente sensível para o crescimento da árvore. Outras medidas são então preferidas. O Índice de Gini, por exemplo, é dado por

$G = \sum_{k=1}^{K} (\hat{p}_{mk}) (1 - (\hat{p}_{mk})),$

sendo uma medida de variância total ao longo das classes $K$ . Um valor baixo indica que um nó contém observações predominantes de uma única classe.

Uma alternativa ao índice de Gini é a entropia:

$D = - \sum_{k=1}^{L} (\hat{p}_{mk}) log (\hat{p}_{mk}),$

Qualquer uma das duas pode ser utilizada para avaliar a qualidade de uma divisão particular, dado que as mesmas são mais sensíveis à pureza do nó do que a taxa de erro de classificação.

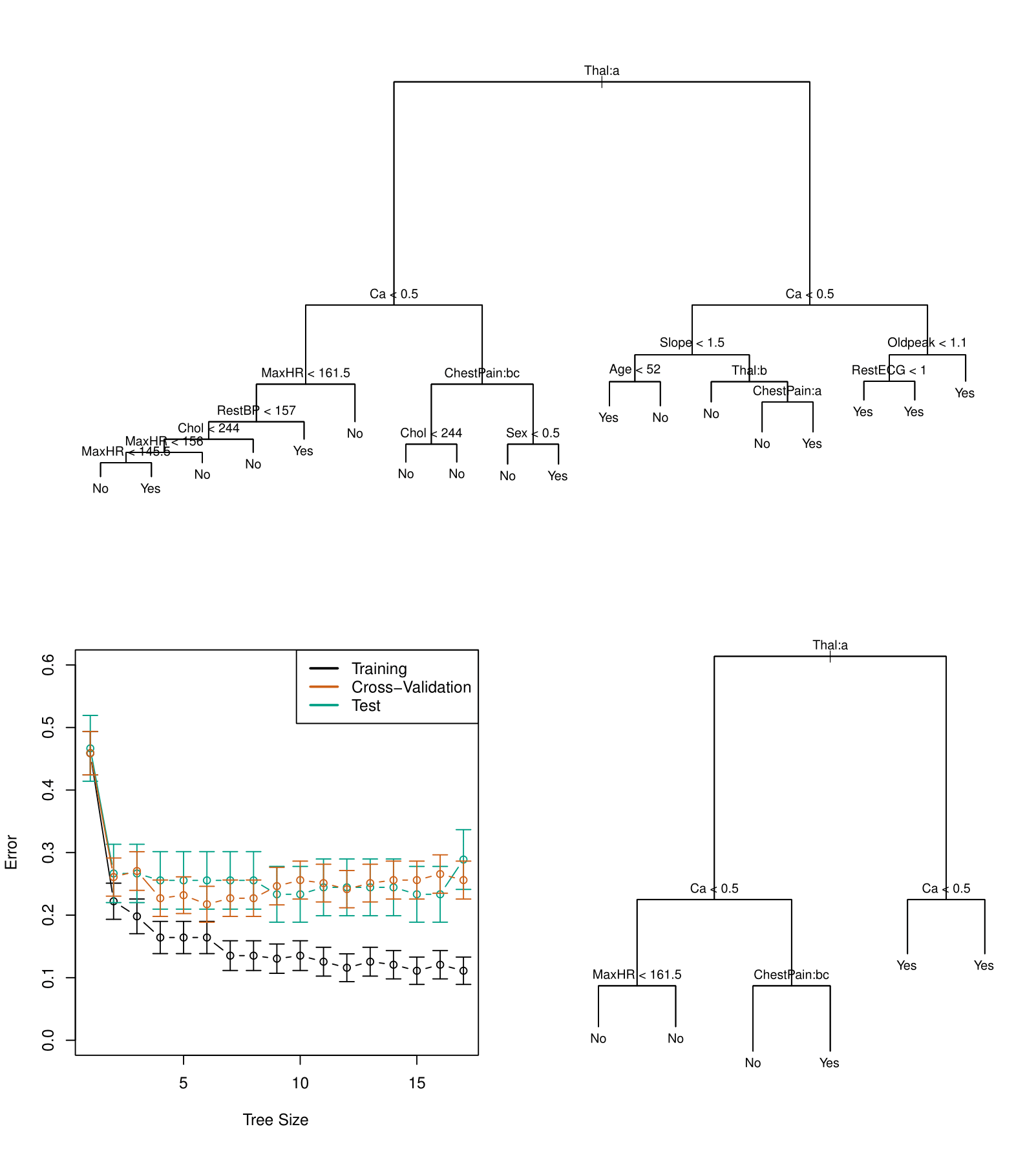
Considere abaixo o dataset Heart. Ele contêm um resultado binário AHD para 303 pacientes que apresentaram dor no peito.

array(['No', 'Yes'], dtype=object)

O valor Yes indica a presença de doença cardíaca no teste de angiográfico, enquanto No indica sem doença. A figura a seguir ilustra um exemplo de árvore sobre esse dataset.

Exemplo de Árvores de Regressão: previsão de preço de carros usados

Nesta seção apresentamos um exemplo do algoritmo Árvores de Regressão.

O problema que utilizaremos para exemplificar é o seguinte:

Deseja-se definir o preço de venda de carros usados.

Os dados utilizados para abordar esse problema são os seguintes:

Conjunto de dados Kelly Blue Book disponibilizado neste link, contendo uma amostra de dados de 804 carros da fabricante GM do ano de 2005.

Não houve nenhum pré-processamento nos dados.

Uma pequena análise exploratória é exibida abaixo:

╭──────────────────────────────────────────────── skimpy summary ─────────────────────────────────────────────────╮
│          Data Summary                Data Types                                                                 │
│ ┏━━━━━━━━━━━━━━━━━━━┳━━━━━━━━┓ ┏━━━━━━━━━━━━━┳━━━━━━━┓                                                          │
│ ┃ dataframe         ┃ Values ┃ ┃ Column Type ┃ Count ┃                                                          │
│ ┡━━━━━━━━━━━━━━━━━━━╇━━━━━━━━┩ ┡━━━━━━━━━━━━━╇━━━━━━━┩                                                          │
│ │ Number of rows    │ 804    │ │ int32       │ 17    │                                                          │
│ │ Number of columns │ 18     │ │ float64     │ 1     │                                                          │
│ └───────────────────┴────────┘ └─────────────┴───────┘                                                          │
│                                                     number                                                      │
│ ┏━━━━━━━━━━━━━━━━━┳━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┓  │
│ ┃ column_name     ┃ NA  ┃ NA %   ┃ mean    ┃ sd     ┃ p0     ┃ p25     ┃ p50     ┃ p75    ┃ p100   ┃ hist    ┃  │
│ ┡━━━━━━━━━━━━━━━━━╇━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━━┩  │
│ │ Price           │   0 │      0 │   21000 │   9900 │   8600 │   14000 │   18000 │  27000 │  71000 │  ▇▃▂▁   │  │
│ │ Mileage         │   0 │      0 │   20000 │   8200 │    270 │   15000 │   21000 │  25000 │  50000 │  ▂▃▇▃▁  │  │
│ │ Cylinder        │   0 │      0 │     5.3 │    1.4 │      4 │       4 │       6 │      6 │      8 │ ▇  ▆ ▂  │  │
│ │ Doors           │   0 │      0 │     3.5 │   0.85 │      2 │       4 │       4 │      4 │      4 │ ▂    ▇  │  │
│ │ Cruise          │   0 │      0 │    0.75 │   0.43 │      0 │       1 │       1 │      1 │      1 │ ▃    ▇  │  │
│ │ Sound           │   0 │      0 │    0.68 │   0.47 │      0 │       0 │       1 │      1 │      1 │ ▃    ▇  │  │
│ │ Leather         │   0 │      0 │    0.72 │   0.45 │      0 │       0 │       1 │      1 │      1 │ ▃    ▇  │  │
│ │ Buick           │   0 │      0 │     0.1 │    0.3 │      0 │       0 │       0 │      0 │      1 │ ▇    ▁  │  │
│ │ Cadillac        │   0 │      0 │     0.1 │    0.3 │      0 │       0 │       0 │      0 │      1 │ ▇    ▁  │  │
│ │ Chevy           │   0 │      0 │     0.4 │   0.49 │      0 │       0 │       0 │      1 │      1 │ ▇    ▅  │  │
│ │ Pontiac         │   0 │      0 │    0.19 │   0.39 │      0 │       0 │       0 │      0 │      1 │ ▇    ▂  │  │
│ │ Saab            │   0 │      0 │    0.14 │   0.35 │      0 │       0 │       0 │      0 │      1 │ ▇    ▁  │  │
│ │ Saturn          │   0 │      0 │   0.075 │   0.26 │      0 │       0 │       0 │      0 │      1 │ ▇    ▁  │  │
│ │ convertible     │   0 │      0 │   0.062 │   0.24 │      0 │       0 │       0 │      0 │      1 │ ▇    ▁  │  │
│ │ coupe           │   0 │      0 │    0.17 │   0.38 │      0 │       0 │       0 │      0 │      1 │ ▇    ▂  │  │
│ │ hatchback       │   0 │      0 │   0.075 │   0.26 │      0 │       0 │       0 │      0 │      1 │ ▇    ▁  │  │
│ │ sedan           │   0 │      0 │    0.61 │   0.49 │      0 │       0 │       1 │      1 │      1 │ ▅    ▇  │  │
│ │ wagon           │   0 │      0 │    0.08 │   0.27 │      0 │       0 │       0 │      0 │      1 │ ▇    ▁  │  │
│ └─────────────────┴─────┴────────┴─────────┴────────┴────────┴─────────┴─────────┴────────┴────────┴─────────┘  │
╰────────────────────────────────────────────────────── End ──────────────────────────────────────────────────────╯

As previsões produzidas pelo algoritmo são exibidas abaixo:

array([12649.11, 11115.01, 20538.09, 22100.39, 19471.97])

Por fim reportamos algumas medidas de acurácia:

158.9182223406238
10643.560047723071

Conclusão

Neste artigo mostramos como precificar carros usados usando Árvores de Decisão. Apresentamos como funciona o método, exploramos as fórmulas, as visualizações gráficas e demonstramos as aplicações em R e Python.

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Referências

G. James, D. Witten, T. Hastie, and R. Tibshirani. An Introduction to Statistical Learning with applications in R. Springer, 2017.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise de impacto fiscal sobre o dolár com Python

Resultado IBC-br - Outubro/2024

Resultado PMC - Outubro/2024

Como usar Inteligência Artificial para Ler as Atas do COPOM?

Resultado PMS - Outubro/2024

Resultado IPCA - Novembro/2024

Outros artigos relacionados

Análise de impacto fiscal sobre o dolár com Python

Usamos uma cesta de 12 moedas para construir um cenário contrafactual da taxa de câmbio após o último anúncio de pacote fiscal, com base em modelagem Bayesiana. No período, o dolár depreciou quase 5% e passou os R$ 6,15, enquanto que na ausência da intervenção a moeda deveria estar cotada em R$ 5,78.

Resultado IBC-br - Outubro/2024

A Análise Macro apresenta os resultados da IBC-br de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Resultado PMC - Outubro/2024

A Análise Macro apresenta os resultados da PMC de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!