Encontrar um modelo com performance adequada para o problema a ser resolvido é um dos grandes desafios de trabalhar com modelos preditivos. Felizmente, existem diversas técnicas e métodos que servem para testar a acurácia dos modelos. A implementação é geralmente simples e pode auxiliar na descoberta do modelo mais adequado. Entretanto, o entendimento do contexto, dos dados, do problema e de outros fatores não é nada simples, mas é fundamental para o uso correto dessas técnicas e métodos. Infelizmente, não existe uma regra geral para seguir cegamente.
Nesse artigo abordamos técnicas de reamostragem de dados, conhecidas como separação treino/validação/teste, úteis para avaliar a acurácia de modelos preditivos. Mostramos exemplos e aplicações das técnicas, destacando o contexto e os desafios que podem emergir, usando problemas de regressão e de classificação com dados temporais e de corte transversal. Códigos dos exemplos são expostos nas linguagens de programação R e Python.
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
Por que separar os dados em amostras?
A ideia geral de separar uma tabela de dados em duas amostras (vamos entender adiante sobre a terceira amostra) é simular como um modelo preditivo estimado/treinado se comporta para dados ainda não conhecidos. O modelo produz previsões acuradas? É preciso testar!
Se o objetivo é previsão, essa separação faz total sentido. Queremos encontrar um modelo que produza previsões para dados futuros/desconhecidos com erro relativo mínimo. Dessa forma, “alimentamos” o modelo com uma parte dos dados, a chamada amostra de treino. A tarefa do modelo é encontrar padrões e relações que melhor se aproximem ou descrevem a variável alvo com base nesses dados. Isso é tudo que o modelo sabe fazer. Ao perguntar para o modelo sobre os dados de treino ele responderá com bastante precisão sobre o valor esperado da variável alvo.
No entanto, queremos saber sobre o futuro. Nesse caso, como avaliar o modelo? Para isso podemos utilizar o modelo para produzir previsões para o restante dos dados, a chamada amostra de teste. Com previsões geradas para períodos ou dados desconhecidos pelo modelo, abre-se a possibilidade de calcular o erro do modelo entre os valores observados e os valores previstos. Ao comparar o erro de previsão de vários modelos, podemos escolher um para trabalhar de fato (em um cenário não simulado).
Portanto, ao separar os dados em amostras de treino e teste, estamos coletando amostras dos dados completos. Reamostragem é um outro nome comum para este procedimento e existem algumas técnicas disponíveis. Vamos tratar delas a seguir.
Técnicas de reamostragem
As técnicas de reamostragem servem para separar um conjunto de dados em amostras, com objetivo final de avaliar a acurácia de modelos preditivos. As técnicas são relativamente parecidas em desenho (separação treino/validação/teste), mas podem diferir na forma, ou seja, quais dados serão alocados em qual amostra. Vamos entender o desenho primeiro.
Suponha que você foi contratado pela maior rede de pet shop do país para criar um sistema de recomendação de produtos para os clientes que são tutores de cachorros e gatos. A empresa forneceu um conjunto de dados com algumas informações (peso, cor, sexo, idade, porte, se usa caixa de areia, data e dados da última compra, etc.) sobre os animais dos seus clientes, conforme o cadastro que os mesmos fazem no app/site.

O problema a ser resolvido, inicialmente, é determinar com base no conjunto de dados se um determinado animal é cachorro ou gato. Com base nessa classificação a empresa poderá desenvolver um sistema de recomendação de produtos para os clientes, visando aumentar a conversão de vendas, receita e outras métricas de interesse.
Esse é um problema de classificação em ciência de dados e podemos utilizar as técnicas de reamostragem, separando os dados em amostras, para encontrar um modelo que melhor classifica os animais.
Separação treino e teste
Você começou o trabalho separando o conjunto de dados em dois: uma parte considerável e suficiente para estimar/treinar um modelo de classificação (i.e., regressão logística), e a outra parte para testar as previsões geradas pelo modelo. Ao final obtém-se uma avaliação de acurácia do modelo, com métricas de erro.

Separação treino-validação-teste
Separar os dados em amostras de treino e teste para avaliar um modelo não é, em geral, suficiente. Relembre-se que queremos encontrar o melhor modelo, em termos de acurácia, portanto é recomendável comparar o desempenho individual de vários modelos — tal como em uma competição esportiva.
De forma análoga, podemos comparar a acurácia de vários modelos dividindo os dados em amostras. Usamos, necessariamente, uma amostra de treino para estimar/treinar os modelos; e usamos uma outra amostra para verificar a acurácia de cada modelo, permitindo a comparação e seleção do melhor. Essa amostra é comumente chamada de amostra de validação, pois é com ela que diferentes (hiper)parâmetros de diferentes modelos podem ser testados, até que se encontre os parâmetros que melhor generalizam para dados não vistos (da amostra de validação).
Por fim, após selecionar o melhor modelo usando a amostra de validação, podemos fazer uma espécie de dupla checagem das previsões desse modelo com dados não vistos, a chamada amostra de teste. Nessa amostra não constam os dados de treino ou de validação, e ela serve para mensurar a acurácia final do modelo escolhido para previsão. Se o modelo escolhido não generalizou bem na amostra de teste, significa que pode ter acontecido uma falha no processo (i.e., vazamento de dados).

Como decidir quais dados vão para quais amostras?
Entendido o desenho, agora vamos falar sobre a forma. As imagens acima ilustram didaticamente o conjunto de dados do exemplo de problema de classificação, ou pelo menos dão uma ideia da distribuição dos dados que podemos encontrar na vida real.
Ter um entendimento sobre a distribuição dos dados é fundamental no momento de separar as amostras e uma análise exploratória pode ajudar nessa etapa. A razão é que separar as amostras não é tão simples quanto apenas aplicar uma regra, por exemplo, 60/20/20 ou 80/10/10 ou qualquer outra regra facilmente encontrada por aí. Em verdade, o tamanho de cada amostra é discutível e menos importante que o conteúdo. Vamos entender isso de acordo com algumas situações que podem acontecer no mundo real.
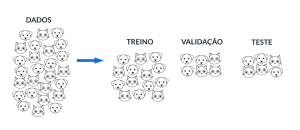
Situação 1: muitos cães e gatos aleatórios
Se existirem dados em grande volume e para problemas em que a ordenação não é relevante, é seguro separar os dados aleatoriamente em amostras de treino-validação-teste. Por definição de probabilidade, cada amostra terá proporções equivalentes de dados para cada categoria (cachorro, gato, etc.), evitando que, por exemplo, uma amostra em específico seja povoada com os dados de apenas uma categoria. Isso seria um problema, pois, em princípio, queremos testar as previsões do modelo para todas as categorias.
Nessa situação, de grande volume de dados, a separação de amostras deve ser por amostragem aleatória simples. Isso não significa colocar as primeiras X linhas na amostra de treino, as próximas Y linhas na amostra de validação e as restantes Z linhas na amostra de teste. Se os dados estiverem ordenados, a chance de uma determinada amostra ser povoada com dados de uma única categoria pode ser alta.
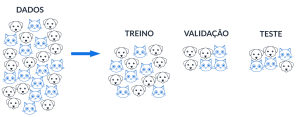
Situação 2: poucos cães e gatos aleatórios
Se a disponibilidade de dados não for grande, é necessário tomar precauções para separar as amostras de treino-validação-teste aleatoriamente. Se, por exemplo, o conjunto de dados é dominado por uma determinada categoria (i.e., gato), então é provável que uma das amostras não seja povoada por todas as categorias.
Nessa situação, de pouco volume de dados, a separação de amostra pode ser categoria-por-categoria. Isso significa separar aleatoriamente da categoria predominante, (i.e., gato), X linhas para amostra de treino, Y linhas para amostra de validação e Z linhas para amostra de teste. E fazer o mesmo procedimento para as demais categorias. Isso se chama amostragem aleatória estratificada.
Situação 3: mesmos dados, objetivo diferente
Agora vamos supor que o conjunto de dados é o mesmo, mas o dono da rede de pet shops está interessado em saber quantas gramas de ração devem ser recomendadas para o cliente adquirir no futuro. O problema passa a ser, além de classificar o animal, prever quantitativamente o consumo de ração ao longo do tempo.
Nessa situação, o ordenamento dos dados importa, caracterizando uma estrutura de dados de série temporal. Se separarmos os dados em amostras aleatórias de treino-validação-teste, perderemos completamente a indexação temporal. Isso é um problema pois queremos uma previsão para o futuro, mas se as amostras estiverem povoadas com períodos aleatórios, o modelo pode não entender padrões e características possivelmente importantes para a solução do problema (i.e., sazonalidade, autocorrelação, etc.).
Nesse caso, devemos fazer a separação de amostras por períodos no tempo. Por exemplo, se houverem 12 meses de dados históricos de compras, podemos colocar os 8 primeiros meses na amostra de treino, os 2 meses seguintes na amostra de validação e os 2 últimos meses na amostra de teste.

Exemplos práticos com dados econômicos
Agora vamos demonstrar essas técnicas de reamostragem com dados reais, no contexto econômico. Utilizaremos os dados da Pesquisa Nacional por Amostra de Domicílios Contínua (PNAD-C) do IBGE, que disponibiliza os microdados da pesquisa. Abaixo apresentamos a estrutura da tabela:
R
(omitido)
Python
Código
Ano Trimestre UF ... V1028199 V1028200 ID_DOMICILIO
0 2022 4 11 ... 298.760783 0.0 1100000160110
1 2022 4 11 ... 298.760783 0.0 1100000160110
2 2022 4 11 ... 158.839984 0.0 1100000160210
3 2022 4 11 ... 281.073395 0.0 1100000160310
4 2022 4 11 ... 281.073395 0.0 1100000160310
[5 rows x 421 columns]Os dados da PNAD-C são amostrais, sendo necessário considerar o plano amostral para obter estimativas estatísticas. Nesse artigo ignoramos isso e focamos apenas em demonstrar as técnicas de separação de amostras.
Pode-se dizer que a tabela é de dados de corte transversal e vamos supor que a variável alvo de previsão seja a V2007 (sexo, conforme o dicionário da pesquisa, 1 = homem e 2 = mulher).
Como o volume de dados é considerável, podemos utilizar a técnica de separação de amostras de treino-validação-teste para um modelo preditivo usando amostragem aleatória simples, conforme abaixo:
R
Código
Total: 478091 (Completa)
V2007 Freq proporcao
1 1 232029 0.4853239
2 2 246062 0.5146761
Total: 286854 (Treino)
V2007 Freq proporcao
1 1 139000 0.4845671
2 2 147854 0.5154329
Total: 95618 (Validação)
V2007 Freq proporcao
1 1 46518 0.4864984
2 2 49100 0.5135016
Total: 95619 (Teste)
V2007 Freq proporcao
1 1 46511 0.4864201
2 2 49108 0.5135799Python
Código
Total: 478091 (Completa)
V2007 proporcao1
V2007
2 246062 0.514676
1 232029 0.485324
Total: 286853 (Treino)
V2007 proporcao1
V2007
2 147731 0.515006
1 139122 0.484994
Total: 95619 (Validação)
V2007 proporcao1
V2007
2 49346 0.516069
1 46273 0.483931
Total: 95619 (Teste)
V2007 proporcao1
V2007
2 48985 0.512294
1 46634 0.487706O procedimento é simples, gera as três amostras com os tamanhos de escolha (impressos acima) e há possibilidade de utilizar semente de reprodução. Observe que a proporção das categorias é preservada, por construção probabilística.
Agora vamos supor que fosse necessário fazer a amostragem aleatória estratificada e que o estrato seja a variável indicativa se o indivíduo sabe ler/escrever (variável V3001 do dicionário). Abaixo fazemos o mesmo procedimento, porém definindo a coluna de estrato como base para separar as amostras:
R
Código
Total: 478091 (Completa)
V2007 V3001 Freq proporcao
1 1 1 193099 0.40389591
2 2 1 210540 0.44037641
3 1 2 24796 0.05186460
4 2 2 22051 0.04612302
Total: 286854 (Treino)
V2007 V3001 Freq proporcao
1 1 1 115953 0.40422305
2 2 1 126231 0.44005313
3 1 2 14981 0.05222517
4 2 2 13126 0.04575847
Total: 95618 (Validação)
V2007 V3001 Freq proporcao
1 1 1 38674 0.40446359
2 2 1 42053 0.43980213
3 1 2 4895 0.05119329
4 2 2 4475 0.04680081
Total: 95619 (Teste)
V2007 V3001 Freq proporcao
1 1 1 38472 0.40234681
2 2 1 42256 0.44192054
3 1 2 4920 0.05145421
4 2 2 4450 0.04653887Python
Código
Total: 450486 (Completa)
V2007 V3001 proporcao1 proporcao2
1.0 217895 403639 0.483689 0.896008
2.0 232591 46847 0.516311 0.103992
Total: 270290 (Treino)
V2007 V3001 proporcao1 proporcao2
1.0 130713 242339 0.483603 0.896589
2.0 139577 27951 0.516397 0.103411
Total: 90098 (Validação)
V2007 V3001 proporcao1 proporcao2
1.0 43536 80571 0.483207 0.89426
2.0 46562 9527 0.516793 0.10574
Total: 90098 (Teste)
V2007 V3001 proporcao1 proporcao2
1.0 43646 80729 0.484428 0.896013
2.0 46452 9369 0.515572 0.103987Conforme pode ser visto, as proporções de cada categoria são mantidas para as diferentes amostras, o que pode ser fundamental para testar as previsões de um modelo.
Por fim, vamos exemplificar como separar amostras por tempo. Os dados de exemplo são do Índice Nacional de Preços ao Consumidor Amplo (IPCA), em frequência mensal, de janeiro de 2000 a dezembro de 2022, a unidade de medida é variação % e a fonte é o IBGE. Abaixo apresentamos a estrutura da tabela:
R
Código
# A tibble: 6 × 2
date ipca
<date> <dbl>
1 2000-01-01 0.62
2 2000-02-01 0.13
3 2000-03-01 0.22
4 2000-04-01 0.42
5 2000-05-01 0.01
6 2000-06-01 0.23Python
Código
ipca
Date
2000-01-01 0.62
2000-02-01 0.13
2000-03-01 0.22
2000-04-01 0.42
2000-05-01 0.01Para séries temporais é mais comum a separação treino-teste somente, mesmo que também seja possível acrescentar a etapa de validação. Abaixo fazemos a separação treino-teste usando, como exemplo, o valor inteiro da frequência da série como tamanho amostral da amostra de teste:
R
Código
| date | ipca |
|---|---|
| 2021-07-01 | 0.96 |
| 2021-08-01 | 0.87 |
| 2021-09-01 | 1.16 |
| 2021-10-01 | 1.25 |
| 2021-11-01 | 0.95 |
| 2021-12-01 | 0.73 |
Código
| date | ipca |
|---|---|
| 2022-01-01 | 0.54 |
| 2022-02-01 | 1.01 |
| 2022-03-01 | 1.62 |
| 2022-04-01 | 1.06 |
| 2022-05-01 | 0.47 |
| 2022-06-01 | 0.67 |
Python
Código
ipca
Date
2021-08-01 0.87
2021-09-01 1.16
2021-10-01 1.25
2021-11-01 0.95
2021-12-01 0.73Código
ipca
Date
2022-01-01 0.54
2022-02-01 1.01
2022-03-01 1.62
2022-04-01 1.06
2022-05-01 0.47Note que a ordenação temporal deve ser preservada.
Conclusão
Nesse artigo abordamos técnicas de reamostragem de dados, conhecidas como separação treino/validação/teste, úteis para avaliar a acurácia de modelos preditivos. Mostramos exemplos e aplicações das técnicas, destacando o contexto e os desafios que podem emergir, usando problemas de regressão e de classificação com dados temporais e de corte transversal. Códigos dos exemplos são expostos nas linguagens de programação R e Python.
Saiba mais
Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:
E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.
Referências
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2021). An introduction to statistical learning. New York: Springer.
Patryk Miziuła. (2021). How You Should Validate Machine Learning Models. https://towardsdatascience.com/how-you-should-validate-machine-learning-models-f16e9f8a8f7a


