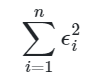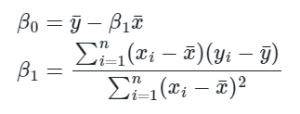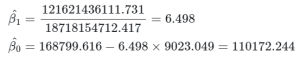Neste texto aprenderemos sobre regressões lineares, o que são, como funcionam e como podem ser usadas. Abordaremos de forma introdutória e objetiva o assunto e assumimos que o leitor possua algum conhecimento prévio sobre álgebra linear, cálculo diferencial e estatística.
Tomaremos como base o livro de Hyndman e Athanasopoulos (2021), que aborda o assunto de maneira prática e introdutória, focando em previsão. Se você precisar ou quiser se aprofundar, veja também Wooldridge (2020) para uma exposição mais detalhada. Este último costuma ser livro-texto de cursos de graduação, especialmente em disciplinas de econometria.
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
O modelo linear
Vamos começar entendendo o que é o modelo de regressão linear, suas aplicações e esclarecer algumas nomenclaturas utilizadas.
O que é?
Uma regressão linear é uma forma de modelar a relação entre variáveis utilizando uma função linear (combinação linear) relativamente simples e interpretável, expressa por meio de uma equação. A ideia básica da regressão linear é que tentamos explicar uma variável y assumindo uma relação linear com outra variável x.
Por exemplo, podemos tentar explicar as vendas mensais, y, de produtos/serviços de uma empresa com base no gasto mensal, x, em publicidade/propaganda.
Aplicações
Alguns exemplos de uso de regressões lineares são:
- Previsão
- Análise de relação entre variáveis
- Análise de tendência
- Análise de elasticidade
Nomenclaturas
A variável do lado esquerdo da equação costuma ser referida como y e pode ter vários nomes a depender do interlocutor: variável dependente, explicada, resposta, endógena.
As variáveis do lado direito da equação costumam ser referidas como x e também podem ter vários nomes: variável independente, explicativa, preditora, regressora, exógena, covariável.
Nesse texto usaremos a nomenclatura variável dependente e independente.
Regressão simples
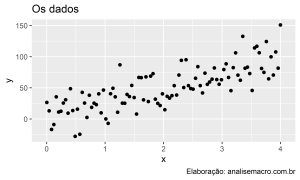
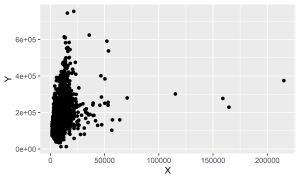
No caso mais simples, a regressão linear relaciona uma variável dependente y e uma única variável independente x. Plotando estas variáveis em um gráfico de dispersão, imagine que o resultado seja esse:
Vamos tomar como exemplo que o y é o preço de imóveis e que o x é a área em metros quadrados. Dessa forma, queremos prever o preço de imóveis com base na área dos mesmos. Em outras palavras, queremos relacionar estas variáveis usando regressão linear, o que significa que queremos encontrar uma linha (reta) que, quando desenhada no gráfico, melhor relacione as variáveis.
Existem muitas possibilidades de linhas para representar a relação entre as variáveis. Das opções abaixo, qual seria a que melhor cumpre esse objetivo?
Seria a linha azul, verde, azul, nenhuma? Uma linha horizontal? Vertical?
É razoável dizer que a linha verde parece ser a reta que melhor relaciona os dados, pois ela é a reta que está menos distante da maioria das observações. E é exatamente isso, ilustrado didaticamente no gráfico acima, que o modelo de regressão linear tenta fazer ao relacionar as variáveis y e x: encontrar uma reta que minimize a distância da mesma com os pontos de dados.
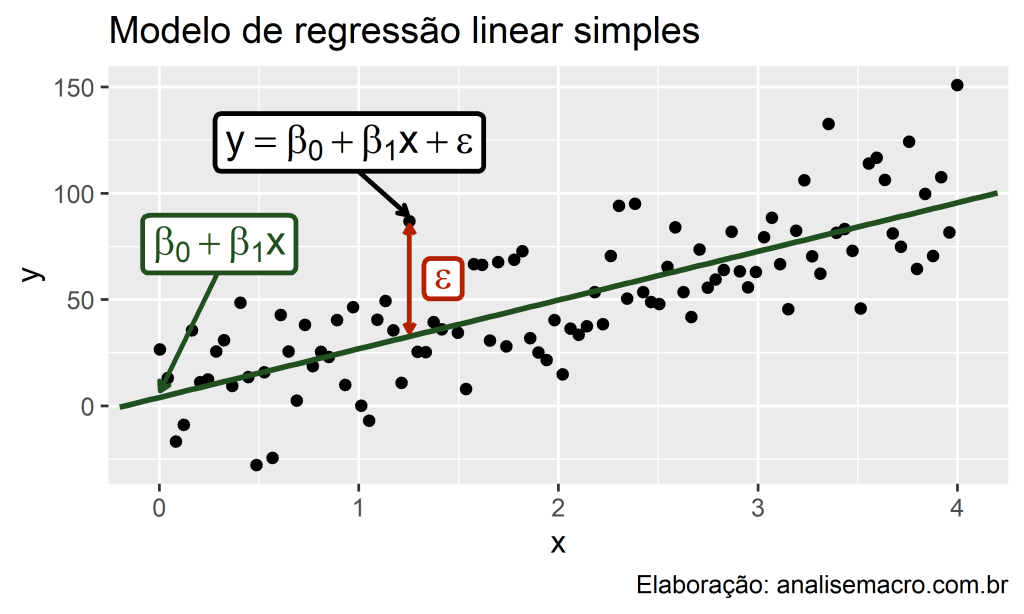
A equação do modelos de regressão linear simples pode ser representada conforme abaixo:
Os coeficientes Beta_0 e Beta_1 são o intercepto e a inclinação da reta, respectivamente, e podem ser entendidos como:
- Beta_0 representa o valor esperado de y quando x=0;
- Beta_1 representa a mudança média esperada em y resultante de um aumento de uma unidade em x.
O termo e é o erro do modelo, ou seja, a distância entre os valores observados e os valores estimados (e=y−(Beta_0+Beta_1x)), pode ser entendido como aquilo que o modelo não consegue explicar (existem muitos detalhes técnicos sobre esse termo que iremos omitir aqui).
Visualmente, estes termos correspondem aos elementos destacados neste gráfico:
Regressão múltipla
A regressão linear múltipla é uma extensão natural do caso simples para quando há mais de uma variável independente no modelo. A representação geral desse modelo é:
Onde y é a variável a ser explicada pelas variáveis independentes x_1, x_2, ⋯, x_k. Vale dizer que o termo de erro e não significa um “equívoco”, mas apenas o desvio da “reta” de ajuste do modelo (nesse caso a representação gráfica teria múltiplas dimensões). Ele captura tudo que pode afetar y mas não está presente em x_k.
Na regressão múltipla, cada coeficiente Beta_1, Beta_2, ⋯, Beta_k do modelo mede o efeito de cada variável independente após levar em conta o efeito de todas as demais variáveis do modelo. Sendo assim, dizemos que cada coeficiente mede o efeito marginal das variáveis independentes. Ao analisá-los individualmente costumam-se utilizar a expressão ceteris paribus, que significa “tudo o mais constante”.
Premissas
Quando usamos o modelo de regressão linear, implicitamente assumimos algumas premissas sobre a equação anterior. Aqui vamos destacar algumas delas:
Primeiro, assumimos que o modelo é uma aproximação razoável da realidade, ou seja, a relação entre a variável dependente e as variáveis independentes satisfazem essa equação linear.
Segundo, assumimos as seguintes premissas sobre o termo de erro e da regressão:
- Erros têm média zero, caso contrário, os valores previstos de y serão sistematicamente tendenciosos;
- Erros não são autocorrelacionados, caso contrário, as previsões serão ineficientes, pois haveria mais informações nos dados que poderiam ser exploradas;
- Erros não têm relação com as variáveis independentes, caso contrário, haveria mais informações que deveriam ser incluídas na parte sistemática do modelo.
Também é útil ter os erros distribuídos normalmente com uma variância constante para produzir intervalos de previsão. Vale pontuar que as premissas podem variar conforme o método de estimação dos coeficientes.
O estimador de mínimos quadrados
Para estimar um modelo de regressão linear, geralmente só temos em mãos os dados observados, mas os coeficientes são desconhecidos. Precisamos estimá-los!
Uma maneira (provavelmente a mais utilizada) de estimar os coeficientes do modelo é minimizando o termo de erro. Usando a equação da regressão linear simples, o termo de erro pode ser representado como:
Ou seja, o termo de erro é a diferença entre os valores observados de y e a estimativa (“reta”) do modelo. Sendo assim, a técnica de mínimos quadrados ordinários possibilita encontrar valores para os coeficientes por uma forma eficaz, minimizando a soma dos quadrado dos resíduos (erros), ou seja, minimizando:
Isso é chamado de estimação de mínimos quadrados pois computa o menor valor da soma do quadrado dos resíduos, procedimento que pode ser feito por derivada. Costuma-se utilizar várias abreviações para esse método, como MQO, MMQ ou OLS.
Ao derivar esse problema de minimização em relação a Beta_0 e Beta_1, obtemos que:
Onde ybarra e xbarra é a média amostral de y e x, respectivamente. Veja que não é um bicho de sete cabeças, certo? Vamos fazer um exemplo numérico para facilitar o entendimento.
Exemplo prático: regressão para previsão de preço de imóveis
Agora que você entendeu o básico sobre o assunto, vamos fazer um exercício aplicado de regressão linear.
Conjunto de dados
Usaremos um conjunto de dados sobre imóveis, o conhecido Ames Housing Data, que possui 82 variáveis sobre 2930 imóveis na cidade de Ames, em Iowa (EUA). Entre as variáveis, existe o Preço de Venda (y) e o Tamanho do Lote em m² (x), sendo assim, nosso objetivo será prever y com base em x. Para mais informações sobre os dados veja De Cock (2011).
O modelo a ser estimado é este:
Separação de amostras
Agora vamos separar o conjunto de dados em duas amostras, de treino e de teste, usando amostragem aleatória simples com proporções 70%/30%, respectivamente. Abaixo reportamos a quantidade de linhas em cada caso:
Código
[1] "Treino: 2051 linhas"Código
[1] "Teste: 879 linhas"Pré-processamento de dados
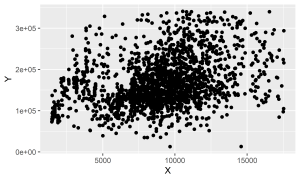
Conforme pode ser observado no gráfico de dispersão acima, existem valores extremos nos dados. Vamos optar por aplicar a regra de corte do IQR, conforme Hyndman e Athanasopoulos (2021), para remover estes valores dos conjuntos de dados. Abaixo plotamos um gráfico de dispersão usando a amostra de treino após esse pré-processamento:
Código
Código
[1] "Treino: 1887 linhas"Código
[1] "Teste: 792 linhas"
Estimação MQO “na mão”
Vamos focar em aprender primeiro a mecânica do método de mínimos quadrados ordinários, fazendo os cálculos “na mão”, com a ajuda de uma planilha eletrônica. Após aprender o fundamento do método, iremos expor os códigos, usando linguagem de programação, que fazem tudo automaticamente!
O procedimento abaixo é para finalidade didática, para entender o que o código faz. Se você já conhece o método é seguro pular essa etapa.
- Baixe os dados da amostra de treino em formato CSV por esse link.
- Faça o login na sua conta do Google, navegue até o Google Drive e faça o upload do arquivo CSV.
- Abra o arquivo de dados CSV no Google Planilhas (Sheets).
- Adicione, conforme a imagem, os nomes para novas colunas e, no final da tabela, linhas para Soma, Média e Beta 1 e Beta 0 para finalidade de calcular os termos das fórmulas acima (ocultamos várias linhas para caber na imagem).
- Comece calculando a média das colunas Y e X e armazene o resultado no final da tabela, conforme a imagem.
- Prossiga calculando cada valor de Y e X menos a média correspondente (o valor da média deve ser fixado na fórmula) e armazene o resultado nas colunas D (X - Xméd) e E (Y - Yméd), conforme a imagem.
- Na coluna da direita, F, multiplique os valores de D (X - Xméd) pelos valores de E (Y - Yméd), conforme a imagem.
- Na última coluna, G, calcule o quadrado da coluna D (X - Xméd), conforme a imagem.
- Prossiga calculando a soma das duas últimas colunas, F e G, e armazene o resultado no final da tabela, conforme a imagem.
- Por fim, podemos calcular os coeficientes começando pelo Beta 1, basta aplicar a fórmula acima, conforme a imagem.
- Finalize calculando o coeficiente Beta 0 aplicando a fórmula da imagem.
Viu só? Nem doeu e agora você sabe fazer uma regressão linear “no braço” (nem todo mundo sabe)!
Se deu tudo certo você chegou a estes valores:
O chapéu significa que é o coeficiente estimado, pois o coeficiente “verdadeiro” é desconhecido. Dessa forma, este é o simples modelo estimado para o preço dos imóveis em Ames, Iowa:
Se você resolver essa equação substituindo Tamanho do Lote em m2 pelos dados da planilha, é possível obter a reta de ajuste do modelo, conforme o gráfico:
Estimação MQO no R
Agora vamos exemplificar no R a estimação de uma regressão linear simples usando o exemplo acima. Tudo que você precisa fazer é:
- Abrir seu ambiente de programação (RStudio);
- Carregar pacotes e os dados;
- Estimar o modelo com a função
lm()do pacote{stats}.
A função lm() é muito útil pois permite expressarmos o modelo como uma fórmula, ou seja, passamos para o seu primeiro argumento, chamado formula, a expressão tal como o modelo proposto acima, ou seja: y ~ x.
No lado direito da fórmula é o nome da variável dependente e no lado esquerdo, separado pelo til ~, é o nome da variável independente. Além disso, devemos dizer onde os dados estão (em qual objeto) no argumento data. Aqui está o código:
Código
A função lm() estima o modelo da fórmula computando o Beta_0 e o Beta_1, sendo que o Beta_0 é automaticamente adicionado, mesmo que não esteja explicitamente declarado na fórmula. Para detalhes e outras informações verifique a documentação (execute ?lm no Console).
Código
Call:
lm(formula = Y ~ X, data = treino)
Residuals:
Min 1Q Median 3Q Max
-191832 -38373 -11002 35593 185467
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 110172.2442 3965.4968 27.78 <0.0000000000000002 ***
X 6.4975 0.4149 15.66 <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 56770 on 1885 degrees of freedom
Multiple R-squared: 0.1151, Adjusted R-squared: 0.1146
F-statistic: 245.2 on 1 and 1885 DF, p-value: < 0.00000000000000022E são os mesmos valores que calculamos de forma manual anteriormente!
Para finalizar, abaixo utilizamos este modelo estimado para produzir previsões para a amostra de teste e calculamos a métrica de acurácia RMSE para ambas as amostras:
Código
[1] "RMSE de treino: 56738.8266780813"Código
[1] "RMSE de teste: 49921.7191925989"Esse modelo está “bom”? Para fins de previsão, errar a precificação de um imóvel em ~50 mil dólares pode ser muito custoso. Há bastante margem para melhorar o modelo, como adicionando mais variáveis independentes, por exemplo, mas vamos encerrar por aqui por brevidade.
Conclusão
Como estimar uma regressão linear sem linguagem de programação? Nesse texto introduzimos esse modelo fundamental de ciência de dados, abrindo as fórmulas e ajustando uma regressão “na mão”, para que o código pronto não seja uma caixa preta. Usamos como exemplo o problema da precificação de imóveis, com aplicações em R e Python.
Referências
De Cock, D. (2011). Ames, Iowa: Alternative to the Boston housing data as an end of semester regression project. Journal of Statistics Education, 19(3).
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2022-04-01.
Wooldridge, J. M. (2020). Introductory Econometrics: A Modern Approach. Cengage learning.