Há uma euforia no mercado financeiro brasileiro com os juros básicos na mínima histórica. O investidor mediano que mantinha seu portfólio aplicado basicamente em renda fixa viu seu rendimento cair substancialmente nos últimos anos. Com efeito, muitos desses migraram para o mercado de capitais, impulsionando a criação de novas gestoras e assets país à fora. A maior consequência dessa euforia talvez seja o avanço do índice Bovespa, mesmo com o crescimento econômico ainda bastante aquém do esperado.
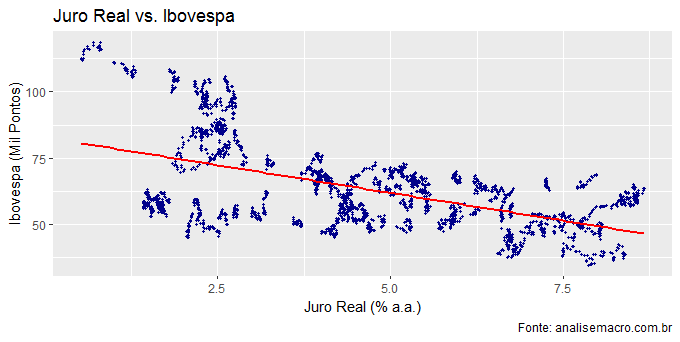
Sabemos da evidência empírica que existe uma correlação negativa entre o índice Bovespa e o juro real. Isto é, menos juro reais estão associados a maiores níveis do índice Bovespa. Isso pode ser facilmente ilustrado com um código de R simples. Abaixo, faço um exemplo.
## Pacotes utilizados nesse comentário library(tidyverse) library(sidrar) library(scales) library(png) library(grid) library(zoo) library(rbcb) library(ggrepel) library(gridExtra) library(readxl) library(xts) library(grDevices) library(ggalt) library(quantmod) library(Quandl)
O script desse comentário começa, como de hábito, com os pacotes que utilizaremos. A seguir, importo o ibovespa, o juro nominal (Selic) e a expectativa de inflação.
## Ibovespa
env <- new.env()
getSymbols("^BVSP",src="yahoo",
env=env,
from=as.Date('2008-12-01'))
ibovespa = env$BVSP[,4]
ibovespa = ibovespa[complete.cases(ibovespa)]
## Juro Real
selic = Quandl('BCB/1178', order='asc', start_date='2008-12-01')
expinf = get_twelve_months_inflation_expectations('IPCA',
start_date = '2008-12-01')
Com as variáveis importadas, é preciso criar o juro real. Isso é feito na sequência.
selic = xts(selic$Value, order.by = selic$Date) expinf12 = xts(expinf$mean[expinf$smoothed=='S'], order.by = expinf$date[expinf$smoothed=='S']) dataex = cbind(selic, expinf12) dataex = dataex[complete.cases(dataex),] juro_ex = (((1+(dataex[,1]/100))/(1+(dataex[,2]/100)))-1)*100
Por fim, eu posso colocá-las em um tibble para gerar um gráfico de correlação como no código abaixo.
## Juntar dados df01 = cbind(ibovespa, juro_ex) df01 = df01[complete.cases(df01),] df01 = tibble(ibovespa=df01[,1], juroreal=df01[,2])
E o gráfico de correlação é posto abaixo.
ggplot(df01, aes(x=juroreal, y=ibovespa/1000))+ geom_point(size=.8, colour='darkblue')+ geom_smooth(method='lm', se=FALSE, colour='red')+ labs(x='Juro Real (% a.a.)', y='Ibovespa (Mil Pontos)', title='Juro Real vs. Ibovespa', caption='Fonte: analisemacro.com.br')
Como dito, há uma correlação negativa entre o índice Bovespa e o juro real. Aí está, basicamente, a raiz da euforia que temos visto no mercado financeiro brasileiro, a despeito do crescimento econômico ainda bastante aquém do desejado. O ponto principal, por suposto, é saber até quando vai essa euforia. E isso passa por saber se o atual nível de juro real será mantido no futuro próximo.
Ao longo dos últimos anos, vimos a aprovação de um conjunto importante de reformas estruturais. Em particular, como visto na edição 71 do Clube do Código, a aprovação do teto de gastos teve como efeito reduzir o juro neutro da economia brasileira - o nível de juro real compatível com hiato do produto nulo em uma Curva IS estacionária.
Um ponto importante, entretanto, é saber o quanto essas reformas irão afetar a capacidade de poupança da economia brasileira. Isto porque, sabemos da teoria e da evidência que a taxa de poupança é um dos fatores mais importantes para determinar o nível de juro do país - ver, por exemplo, The Puzzle of Brazil's High Interest Rates. Infelizmente, como se sabe, a taxa de poupança brasileira é não só baixa como cadente nos últimos anos.
Para ilustrar esse ponto, podemos pegar os dados das Contas Nacionais Trimestrais através do pacote sidrar. O código abaixo implementa.
tab1 = get_sidra(api='/t/2072/n1/all/v/933,940/p/all') pib = tab1$Valor[tab1$`Variável (Código)`==933] poupanca = tab1$Valor[tab1$`Variável (Código)`==940] fbcf = get_sidra(api='/t/1846/n1/all/v/all/p/all/c11255/93406/d/v585%200')$Valor
Com o código acima, pegamos os dados do PIB, da Poupança Bruta e da Formação Bruta de Capital Fixo. A seguir, nós tratamos os dados, de modo a colocar em um tibble as taxas de poupança e de investimento acumuladas em quatro trimestres.
dates_1 = seq(as.Date('1996-01-01'), as.Date('2019-09-01'),
by='3 month')
dates_2 = seq(as.Date('2000-01-01'), as.Date('2019-09-01'),
by='3 month')
df1 = tibble(dates=dates_1, fbcf=fbcf)
df2 = tibble(dates=dates_2, pib=pib, poupanca=poupanca)
data = inner_join(df1, df2, by='dates') %>%
mutate(tx_poupanca = (poupanca+lag(poupanca,1)+lag(poupanca,2)+
lag(poupanca,3))/(pib+lag(pib,1)+lag(pib,2)+lag(pib,3))*100) %>%
mutate(tx_investimento = (fbcf+lag(fbcf,1)+lag(fbcf,2)+
lag(fbcf,3))/(pib+lag(pib,1)+lag(pib,2)+lag(pib,3))*100) %>%
transform(dates = as.yearqtr(dates))
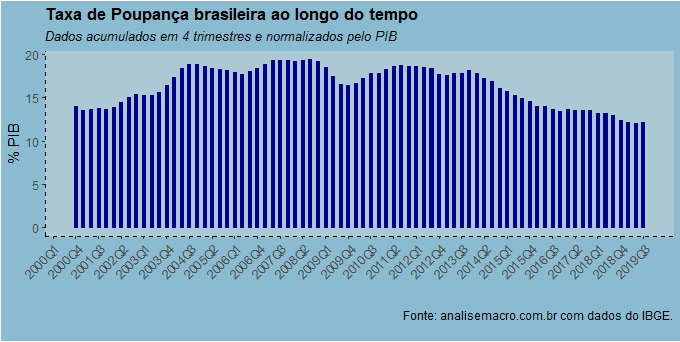
Com os dados prontos, podemos construir o gráfico a seguir.
Como se vê, temos um nível de poupança bastante baixo, mesmo se comparado a outros países de mesmo nível de renda per capita. Há muitas explicações para isso, como a existência de uma ampla rede de proteção social no país, incluindo aí a previdência pública, que desincentivaria a necessidade de poupança para a velhice ou a existência de universidades estatais subsidiadas para a classe média, dentre outras.
A dúvida, portanto, é se as reformas aprovadas ao longo dos últimos anos, bem como as que estão ainda em andamento no Congresso serão suficientes para mudar essa questão institucional estrutural, incentivando as famílias e o governo a aumentarem a poupança no médio e longo prazo. Esse ponto é crucial para saber se o juro que estamos experimentando no momento é de fato permanente ou há risco de voltarmos a flertar com juros nominais de um dígito quando a economia conseguir reduzir a ociosidade.
Não é uma questão simples de responder posto que envolve uma economia política bastante complexa. Em particular, passa pela continuação dos avanços reformistas que vivemos nos últimos anos. E isso não é nada trivial.
A conferir...
__________________________
(*) O código completo desse comentário estará logo mais no Clube do Código.
(**) Aprenda a fazer análises como essa com nossos Cursos Aplicados de R.