O Banco Central voltou a subir juros em meio a choques sobre a inflação. O aumento de juros tem como objetivo, a princípio, afetar o hiato do produto (via Curva IS), tomando a sua diferença em relação ao juro de equilíbrio. A maior ociosidade afeta os preços via Curva de Phillips, o que conclui o objetivo inicial da política monetária.
A despeito do processo acima parecer simples, ele não é, posto que está sujeito à incerteza e, ainda, à defasagens. Tanto não é imediato o efeito do juro sobre o hiato quanto não é do hiato sobre a inflação. Há muita estória por detrás das cortinas que não é o foco desse Comentário de Conjuntura.
Nosso foco aqui é uma espécie de corolário do processo de aumento de juros.
Isto porque, quando o Banco Central começa a subir juros, isso vai ter impacto na diferença entre o juro doméstico e o internacional, geralmente representado pelo juro norte-americano. Em tese, quanto maior essa diferença, maior será a apreciação cambial. Mais apreciação cambial implica em menos pressão para a inflação. Ao menos, para os bens tradeables.
O diferencial de juros aprecia a moeda doméstica porque atrai grana de estrangeiros dispostos a correr o risco de vir a esse país desorganizado chamado Brasil.
A estória que contei acima é muito boa e até que faz sentido. Mas você acreditaria nela?
Bom, eu não sou economista, apesar do bacharelado/mestrado, mas se fosse, digo, se fosse, eu não acreditaria.
Narrativas podem ser desmentidas ao sabor do vento, posto que prefiro meus modelinhos.
Então, antes de contar essa estória aí em cima, eu rodei alguns modelinhos e também li alguma teoria.
A teoria por trás dos modelinhos, certo?
Blz. A ideia aqui é basicamente endogenizar a taxa de câmbio e construir um modelinho que consiga explicar sua trajetória ao longo do tempo. A equação vem de um box do Relatório Trimestral de Inflação do Banco Central e pode ser descrita como segue:
(1)
onde:
é a taxa de câmbio;
é a taxa básica de juros do Br;
é a taxa básica de juros do US;
é uma medida de risco;
é a inflação do Br;
é a inflação do US.
Sobre a equação acima, por suposto, aplicamos a restrição de que , isto é, a variação do câmbio nominal, no equilíbrio, deve ser igual ao diferencial de inflação.
Uma vez que tenhamos a nossa equação e a nossa restrição, podemos colocar a mão na massa. Antes de mais nada, carregamos alguns pacotes.
library(tidyverse) library(ecoseries) library(rbcb) library(quantmod) library(timetk) library(tstools) library(lubridate) library(dynlm) library(restriktor) library(stargazer) library(broom)
E depois vamos à Selva coletar os dados...
## Pegar Selic, IPCA e Câmbio no Banco Central
series = list(selic = 4189, ipca = 433, cambio = 3698)
data = get_series(series) %>%
reduce(inner_join) %>%
mutate(inflacao_br_3m = acum_p(ipca,3))
## Pegar CPI US e FED Funds no FRED St. Louis
cpi_us = quantmod::getSymbols("CPIAUCSL", src='FRED')
cpi_us = timetk::tk_tbl(CPIAUCSL, preserve_index = TRUE, rename_index = "date") %>%
rename(cpi = CPIAUCSL) %>%
mutate(inflacao_us_3m = (cpi/lag(cpi,3)-1)*100)
fed_funds = quantmod::getSymbols("FEDFUNDS", src='FRED')
fed_funds = timetk::tk_tbl(FEDFUNDS, preserve_index = TRUE, rename_index = "date")
## Pegar EMBI no IPEADATA
premio_risco = series_ipeadata(40940, periodicity = 'D') %>%
reduce(inner_join) %>%
rename(date = data, embi = valor) %>%
group_by(date = floor_date(date, 'month')) %>%
summarise(embi = mean(embi))
Uma vez que os dados estejam disponíveis, nós podemos tratá-los e deixá-los em condições de estimar a equação que ilustra esse Comentário.
Para quem tiver interesse nessa parte do código, não se acanhe em conhecer o Clube AM. Todos os códigos de todos os Comentários estão disponíveis lá. Além de outras coisas...
A tabela abaixo ilustra os coeficientes do modelo com restrição.
| Estimate | Std. Error | t value | Pr(> | t| ) | |
| dlcambio_l1 | 0.571 | 0.063 | 9.000 | 0 |
| ddif_juros | -0.538 | 0.312 | -1.723 | 0.089 |
| dlrisco | 0.190 | 0.025 | 7.554 | 0 |
| dif_inflacao | 0.429 | 0.063 | 6.766 | 0 |
Como se vê, o coeficiente do diferencial de juros é negativo, o que implica em apreciação cambial quando o diferencial de juros aumenta. Igualzinho à narrativa que contei acima. O risco por seu turno é positivo, mais risco, mais depreciação cambial, assim como o diferencial de inflação.
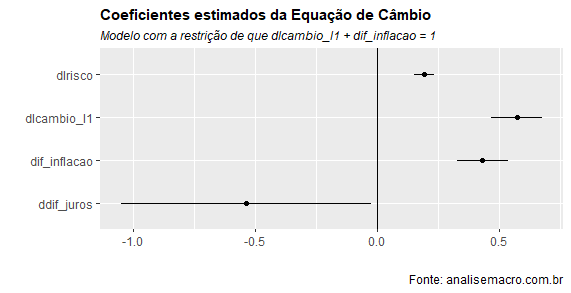
A seguir, colocamos os coeficientes em um gráfico como abaixo. O mesmo gráfico feito em um exercício no hoje extinto Clube do Código sobre repasse cambial, de autoria do Renato Lerípio.
Como se pode ver, há bastante incerteza em relação ao tamanho do coeficiente do diferencial de juros, considerando um IC de 90%.
Para além disso, talvez o mais interessante da macroeconomia seja a interdependência entre as variáveis do sistema, de sorte que o banqueiro central - nesse caso - deva tomar o máximo de cuidado para não acertar o que não viu...
_______________________________