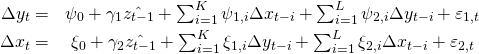Estimando um modelo de correção de erros entre a Produção de Veículos e a Produção Industrial

Uma exceção ao caso de regressão espúria vem à tona quando dois processos aleatórios compartilham a mesma tendência estocástica - para uma demostração detalhada, ver Enders (2009). Para ilustrar, considere, como Verbeek (2012), duas séries integradas de ordem 1, $Y_t$ e $X_t$ , e suponha que exista uma relação linear entre elas, dada por $Y_t = \beta X_t + \epsilon_{Yt}$ . Isso implica no fato de existir algum valor de $\beta$ tal que $Y_t - \beta X_t$ seja integrado de ordem zero, mesmo com as séries originais sendo ambas não estacionárias. Nesses casos, diz-se que as séries são cointegradas e as mesmas compartilham a mesma tendência.

Sendo um pouco mais formal, com base em Pfaff (2008), a ideia por trás do conceito de cointegração é encontrar uma combinação linear entre duas variáveis $I(d)$ de tal sorte que isso leve a uma variável de menor ordem de integração. Isto é,

Os elementos do vetor $x_t$ são ditos cointegrados de ordem $d, b$ , denominado por $x_t \sim CI(d,b)$ , se todos os elementos de $x_t$ são $I(d)$ e o vetor $\alpha (\neq 0)$ existe tal que $z_t = \alpha^{'} x_t \sim I(d-b)$ , onde $b > 0$ . O vetor $\alpha$ é então chamado cointegrante.

Para os economistas, por exemplo, esse tipo de análise permite estabelecer relações de longo prazo entre variáveis não estacionárias. O problema, por suposto, passa a como estimar o vetor cointegrante e como modelar o comportamento dinâmico das variáveis $I(d)$ . Para resolver, vamos ilustrar o método de dois passos de Engle-Granger}, exposto em Pfaff (2008). No primeiro passo, estimamos o seguinte modelo contendo variáveis não estacionárias de mesma ordem de integração.

(1) $\begin{equation*} y_t = \alpha_1 x_{t,1} + \alpha_2 x_{t,2} + \alpha_K x_{t,K} + z_t \end{equation*}$

para $t = 1,...,T$ , onde $z_t$ é um termo de erro. O vetor cointegrante $(K+1)$ $\hat{\alpha}$ estimado é dado por $\hat{\alpha} = [1,-\hat{\alpha^{*}}]^{'}$ , onde $\hat{\alpha^{*}} = (\hat{\alpha_1},...,\hat{\alpha_K})$ . Assim, acaso exista uma relação de cointegração entre as variáveis, $z_t$ nada mais é do que o erro em relação ao equilíbrio de longo prazo entre elas. Nesse caso, $z_t$ será necessariamente estacionário. Pelo fato de $z_t$ ser uma variável estimada, é preciso testar a presença de raiz unitária com outros valores críticos. No R, esses valores podem ser obtidos com a função unitrootTable do pacote fUnitRoots

Se conseguirmos evidências de que $z_t$ é de fato estacionário, podemos passar adiante. O passo seguinte é especificar um modelo de correção de erros (ECM, no inglês). Para simplificar, vamos considerar, como em Pfaff (2008), o caso bivariado, onde $y_t$ e $x_t$ são cointegradas, sendo ambas $I(1)$ . O ECM é então especificado, de forma geral, como segue

(2) $\begin{eqnarray*} \Delta y_t =& \psi_0 + \gamma_1 \hat{z_{t-1}} + \sum_{i=1}^{K} \psi_{1,i} \Delta x_{t-i} + \sum_{i=1}^{L} \psi_{2,i} \Delta y_{t-i} + \varepsilon_{1,t} \\ \Delta x_t =& \xi_0 + \gamma_2 \hat{z_{t-1}} + \sum_{i=1}^{K} \xi_{1,i} \Delta y_{t-i} + \sum_{i=1}^{L} \xi_{2,i} \Delta x_{t-i} + \varepsilon_{2,t} \label{passo22} \end{eqnarray*}$

onde $\hat{z_{t}}$ é o erro do modelo estimado em 1 e $\varepsilon_{1,t}$ $\varepsilon_{2,t}$ são ruídos brancos. Nesses termos, o ECM na equação 2 implica que mudanças em $y_t$ são explicadas pela sua própria estória, mudanças defasadas em $x_t$ e pelos erros obtidos da relação de equilíbrio no passo 1. O valor do coeficiente $\gamma_1$ determina, por suposto, a velocidade de ajustamento e deveria ser sempre negativo. De outra forma, o sistema poderia divergir da sua trajetória de equilíbrio de longo prazo.

Para ilustrar, vamos verificar a relação existente entre a produção de veículos e a produção industrial ao longo do tempo. Abaixo, nós carregamos alguns pacotes do R que utilizaremos nesse Comentário de Conjuntura.


library(ggplot2)
library(xtable)
library(forecast)
library(gridExtra)
library(readxl)
library(dplyr)
library(magrittr)
library(scales)
library(sidrar)
library(vars)
library(dynlm)

Carregados os pacotes, nós podemos importar a produção de veículos e a produção industrial com o código abaixo.


# Produção de Veículos
url = 'http://www.anfavea.com.br/docs/SeriesTemporais_Autoveiculos.xlsm'
download.file(url, destfile = 'veiculos.xlsm', mode='wb')
veiculos = read_excel('veiculos.xlsm', col_types = c('date',
rep('numeric', 25)),
skip=4)
veiculos$X__1 = as.Date(veiculos$X__1, format="%d/%m/%Y")
colnames(veiculos)[1] = 'dates'

## indústria
table1 = get_sidra(api='/t/3653/n1/all/v/3134,3135/p/all/c544/all/d/v3134%201,v3135%201')

geral_sa = table1$Valor[table1$`Variável (Código)`==3134 & table1$`Seções e atividades industriais (CNAE 2.0) (Código)`==129314]

geral = table1$Valor[table1$`Variável (Código)`==3135 & table1$`Seções e atividades industriais (CNAE 2.0) (Código)`==129314]

dates = seq(as.Date('2002-01-01'), as.Date('2019-10-01'), by='1 month')
industria = tibble(dates, geral, geral_sa)

Temos dois tibbles contendo os dados da produção de veículos e da produção industrial. A seguir, nós podemos plotar um gráfico de correlação entre as séries.


filter(veiculos, dates > '2002-01-01') %>%
inner_join(industria, by='dates') %>%
ggplot(aes(x=Produção/1000, y=geral))+
geom_point()+
geom_smooth(se=FALSE, method='lm', colour='red')+
labs(x='Produção de Veículos', y='Produção Industrial',
title='Produção de Veículos vs. Produção Industrial',
caption='Fonte: analisemacro.com.br')

E o gráfico...

De posse dos dados, nós então estimamos a produção industrial contra a produção de veículos e obtemos os resíduos da regressão. Verificamos que os mesmos são estacionários, o que nos permite passar para o passo 2 e estimar o seguinte modelo:

(3) $\begin{align*} \Delta Industria_t = \gamma_0 + \gamma_1 \hat{u_{t-1}} + \gamma_2 \Delta Veiculos_t + \varepsilon_t \end{align*}$

onde $\hat{u_{t-1}}$ são os resíduos da regressão que acabamos de estimar. Abaixo a tabela com os resultados da regressão.


	Dependent variable:

	d(industria)

lag(resid, -1)	-0.250^***
	(0.046)

d(veiculos)	0.0001^***
	(0.00001)

Constant	0.019
	(0.243)


Observations	212
R²	0.644
Adjusted R²	0.641
Residual Std. Error	3.542 (df = 209)
F Statistic	189.114^*** (df = 2; 209)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Como esperado, o coeficiente que dá a velocidade do ajustamento é negativo, bem como o coeficiente da produção de veículos é estatisticamente significativo. Com a recuperação da produção de veículos, é esperado um impacto positivo sobre a produção industrial ao longo do tempo, o que deve contribuir para uma aceleração no crescimento da economia.

________________________________

Enders, W. Applied Econometric Times Series. Wiley Series in Probability and Statistics. Wiley,
2009.

Pfaff, B. Analysis of integrated and cointegrated time series with R. Springer, New York, second
edition, 2008.

Verbeek, M. A Guide to Modern Econometrics. Editora Wiley, 2012.

(*) Isso e muito mais você aprende no nosso Curso de Séries Temporais usando o R.

(**) Os códigos do comentário estarão disponíveis logo mais no Clube do Código.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Transfer Learning: mostrando porque o Python está na ponta do desenvolvimento

Criando Tabelas com o Python: mostrando o poder da linguagem sobre o Excel

Análise do Censo Demográfico com o R

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Criando um Dashboard de análise de Ações no Python

Outros artigos relacionados

Transfer Learning: mostrando porque o Python está na ponta do desenvolvimento

A aprendizagem por transferência (transfer learning) é o reuso de um modelo pré-treinado em um novo problema. Portanto, sua utilização torna-se um avanço enorme para a previsão de diferentes tipos de variáveis, principalmente para aquelas ordenadas no tempo. Mostramos nesta postagem o uso do Transfer Learning com o Python para o caso de Séries Temporais.

Criando Tabelas com o Python: mostrando o poder da linguagem sobre o Excel

Nos dias atuais, pessoas que trabalham com dados estão constantemente confrontados com um dilema: criar uma tabela não tão genial no Excel ou manter em um formato ainda pior, como um dataframe, mas mantendo a flexibilidade de obtenção dos dados. Podemos resolver esse grande problema, unindo a flexibilidade e beleza ao usar a biblioteca great_tables do Python.

Análise do Censo Demográfico com o R

Como podemos analisar dados do Censo Demográfico para produzir pesquisas e implementar políticas públicas? Mostramos nesta postagem o resultado de uma breve análise dos dados preliminares do Censo Demográfico de 2022 usando o R.