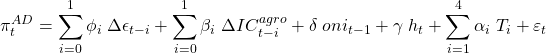No mês de dezembro, iremos lançar uma nova versão do Clube do Código. O projeto de compartilhamento de códigos da Análise Macro vai avançar para uma versão 2.0, que incluirá a existência de uma comunidade no Telegram/Whatsapp, de modo a reunir os membros do Novo Clube, compartilhando com eles todos os códigos dos nossos posts feitos aqui no Blog, exercícios de análise de dados de maior fôlego, bem como tirar dúvidas sobre todos os nossos projetos e Cursos Aplicados de R.
Para ilustrar o que vamos compartilhar lá nesse novo ambiente, vou publicar aqui nos próximos dias alguns dos nossos exercícios completos de análise de dados. Esses exercícios fazem parte do repositório atual do Clube, que irá migrar para o novo projeto. Além de todos os exercícios existentes, vamos adicionar novos exercícios e códigos toda semana, mantendo os membros atualizados sobre o que há de mais avançado em análise de dados, econometria, machine learning, forecasting e R.
Para começar, nesse Comentário de Conjuntura vou replicar um modelo descritivo para a inflação de alimentos. A inflação de alimentos tem sido uma grande incógnita nos últimos anos, influenciando de forma decisiva o erro de previsão da inflação cheia. Isso nos motivou a replicar um modelo do Banco Central do Brasil, exposto em boxe do Relatório de Inflação de junho de 2016, intitulado Evolução recente da inflação de alimentos. O modelo proposto pelo BCB consiste na seguinte equação
(1)
onde é inflação de alimentação no domicílio,
é a variação da taxa de câmbio nominal,
é a variação do segmento de commodities agropecuárias do Índice de Commodities - Brasil (medido em dólares),
é a primeira defasagem da dummy se o mundo está ou não sob efeito do El Niño,
é o hiato do produto e
são dummies sazonais.
Para estimar 1, nosso maior desafio será de coleta e tratamento das variáveis envolvidas. Isso é feito na sequência.
# Coleta e tratamento de dados
Para replicar o modelo proposto em 1, vamos precisar de cinco séries, a saber: a inflação de alimentação no domicílio, o Oceanic Niño Index (ONI), o Produto Interno Bruto, a taxa de câmbio nominal e o Índice de Commodities no seu corte agropecuário. Uma vez obtidas essas séries, elas precisarão ser trimestralizadas e tratadas, de modo a obter as variáveis que serão utilizadas para estimar 1. De modo a replicar os resultados do BCB, vamos obter as séries a partir do primeiro trimestre de 2000.
Antes, porém, o script começa carregando alguns pacotes.
library(BETS) library(ggplot2) library(forecast) library(sidrar) library(gridExtra) library(rsoi) library(xts) library(mFilter) library(dynlm) library(stargazer)
Com efeito, o código abaixo coleta, trata e organiza as séries em uma matriz.
## Obter a série do Oceanic Niño Index (ONI) oni = download_oni() oni = xts(oni$ONI, order.by = oni$Date) oni = window(oni[-1,], start='2000-01-01') oni = ts(apply.quarterly(oni, FUN=mean), start=c(2000,01), freq=4) oni = ifelse(oni>0.5,1,0) ## Obter o Índice de Commodities Agro icagro = BETSget(20050, from='1999-10-01', data.frame = TRUE) icagro = xts(icagro$value, order.by = icagro$date) icagro = ts(apply.quarterly(icagro, FUN=mean), start=c(1999,04), freq=4) dicagro = diff(icagro) ## Obter o PIB e o hiato pib = BETSget(22109, from='2000-01-01', data.frame = TRUE) hiato = ts(hpfilter(pib$value, freq=1600, type='lambda')$cycle, start=c(2000,01), freq=4) ## Obter a taxa de câmbio cambio = BETSget(3697, from='1999-10-01', data.frame = TRUE) cambio = xts(cambio$value, order.by=cambio$date) cambio = ts(apply.quarterly(cambio, FUN=mean), start=c(1999,4), freq=4) dcambio = diff(cambio) ## Obter a inflação de alimentação no domicílio alim01 = get_sidra(api='/t/655/n1/all/v/all/p/all/c315/7171/d/v63%202') alim02 = get_sidra(api='/t/2938/n1/all/v/63/p/all/c315/7171/d/v63%202') alim03 = get_sidra(api='/t/1419/n1/all/v/63/p/all/c315/7171/d/v63%202') alimentos = ts(c(alim01$Valor, alim02$Valor, alim03$Valor), start=c(1999,08), freq=12) fator = 1+alimentos/100 acumulado = (fator*lag(fator,-1)*lag(fator,-2)-1)*100 alimdom = acumulado alimentos = xts(alimdom, order.by = as.Date(time(alimdom))) alimentos = window(alimentos, start='2000-01-01') alimentos = ts(apply.quarterly(alimentos, FUN=mean), start=c(2000,01), freq=4) ## Obter as dummies sazonais dummies = ts(seasonaldummy(alimentos), start=c(2000,01), freq=4) ## Juntar todos os dados em uma matriz data = ts.intersect(alimentos, dcambio, dicagro, oni, hiato, dummies)
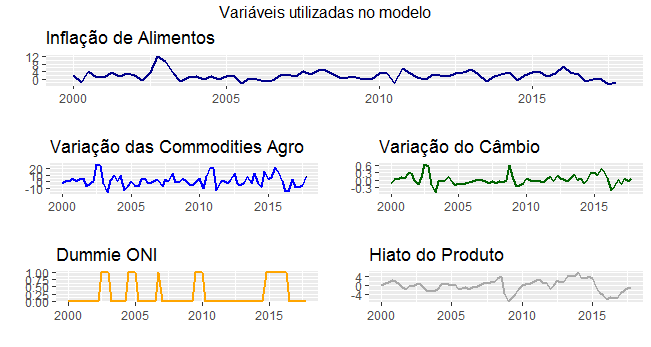
Abaixo, um gráfico das séries já devidamente tratadas.
# Modelo
Com os dados devidamente tratados, podemos estimar o modelo proposto pelo BCB em 1 para o período replicado no boxe - i.e., até o quarto trimestre de 2016. O código abaixo implementa.
modelo = dynlm(alimentos~dcambio+lag(dcambio,-1)+dicagro+ lag(dicagro,-1)+lag(oni,-1)+hiato+ dummies.Q1+dummies.Q2+dummies.Q3, data=data, end=c(2016,01))
A tabela 1 traz os resultados do modelo. A variável defasada da variação do câmbio, as variações do índice de commodities, a variável dummy associada ao ONI e o hiato do produto se mostram estatisticamente significativas para explicar a inflação de alimentação no domicílio. Em particular, o coeficiente da variável dummy é de 1.2, o que implica dizer que o fim do El Niño em um determinado trimestre reduz a inflação de alimentos em 1.2 pontos percentuais no trimestre seguinte.
| Dependent variable: | |
| alimentos | |
| dcambio | -2.342 |
| (1.736) | |
| lag(dcambio, -1) | 3.940** |
| (1.787) | |
| dicagro | 0.061* |
| (0.035) | |
| lag(dicagro, -1) | 0.090** |
| (0.036) | |
| lag(oni, -1) | 1.173* |
| (0.591) | |
| hiato | 0.193** |
| (0.094) | |
| dummies.Q1 | 0.083 |
| (0.666) | |
| dummies.Q2 | -0.305 |
| (0.697) | |
| dummies.Q3 | -0.537 |
| (0.674) | |
| Constant | 1.395*** |
| (0.503) | |
| Observations | 64 |
| R2 | 0.537 |
| Adjusted R2 | 0.460 |
| Residual Std. Error | 1.831 (df = 54) |
| F Statistic | 6.972*** (df = 9; 54) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
______________________