É razoável supor que variáveis como incerteza e utilização da capacidade instalada da indústria de transformação andem juntas. Isto porque, uma vez que haja incerteza sobre o organismo econômico, tudo nos leva a acreditar que a utilização da capacidade instalada será menor. De modo a ilustrar esse movimento, podemos fazer uso das séries da Fundação Getúlio Vargas (FGV) para esses dois indicadores. Como de praxe, vamos carregar alguns pacotes.
library(readr) library(ggplot2) library(scales) library(gridExtra) library(BMR)
Os dados estão disponíveis no arquivo data.csv e são importados com o pacote readr.
data = read_csv2('data.csv',
col_types = list(col_date(format='%d/%m/%Y'),
col_double(),
col_double()))
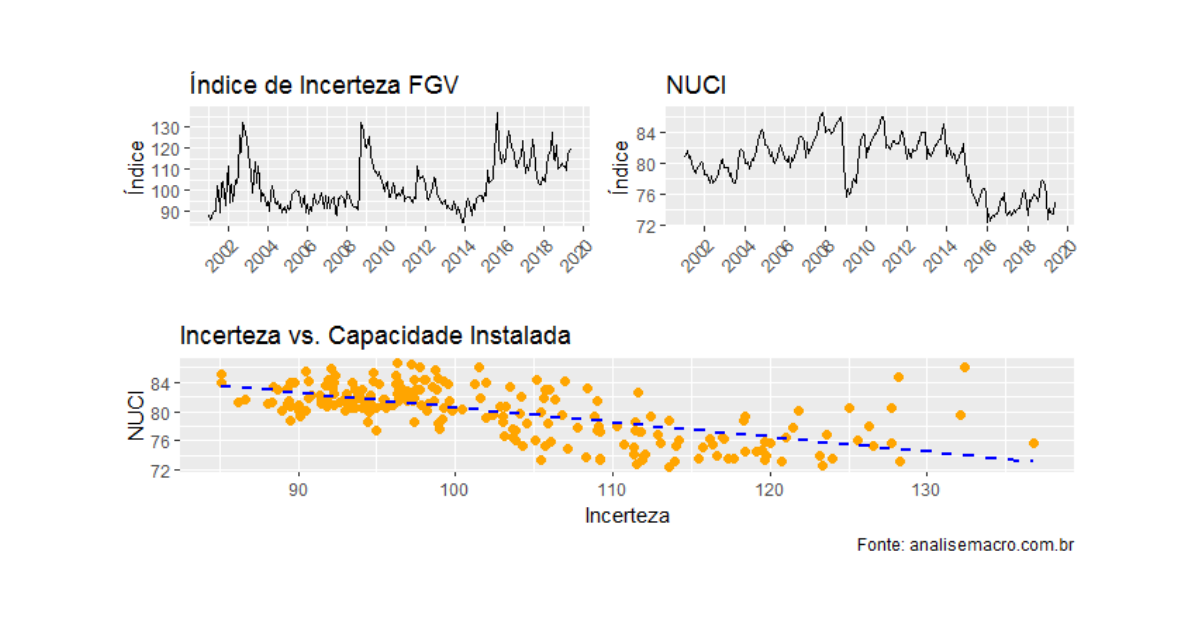
Podemos, então, construir um gráfico com as nossas variáveis como abaixo, de modo a visualizar tanto as séries quanto a relação entre elas.
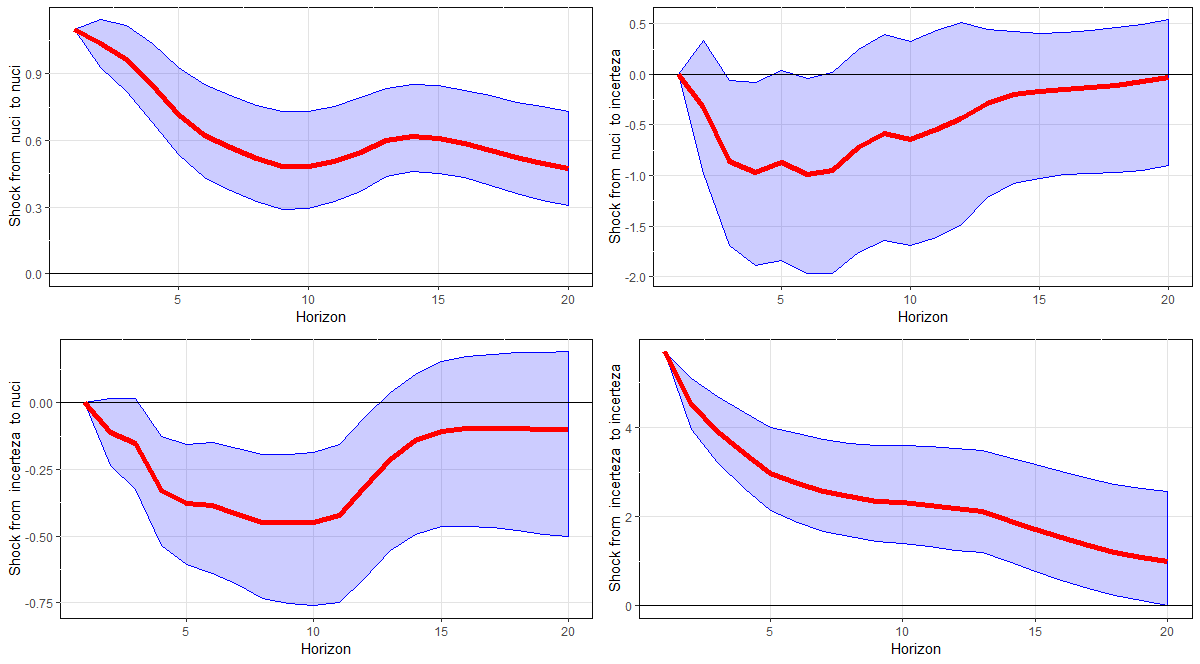
Como se pode ver, existe, de fato, uma relação negativa entre as variáveis. Mais incerteza está relacionada a menos uso da capacidade instalada. Isso visto, estimei um BVAR para ver o efeito de um choque da incerteza sobre a NUCI. As funções de impulso-resposta são colocadas abaixo.
Um choque na incerteza faz a utilização da capacidade instalada ser menor, como pode ser visto pela função impulso-resposta. Em outros termos, para que a economia volte a crescer é peremptório que tenhamos uma redução da incerteza. Contribui para isso um Congresso e um Executivo comprometidos com a agenda de reformas.
____________________
Os códigos desse Comentário estarão disponíveis, como de hábito, no Clube do Código.