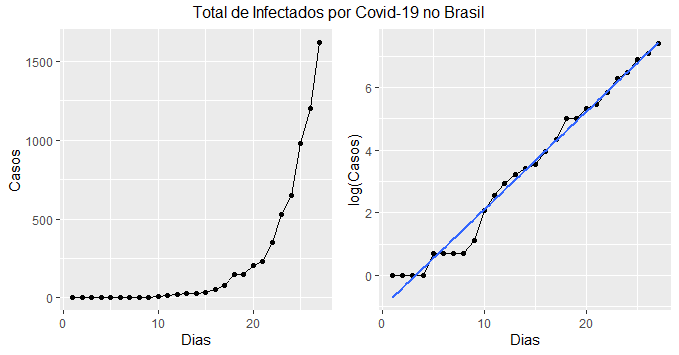
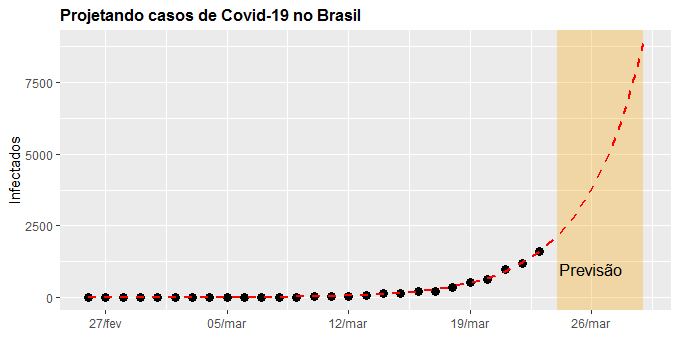
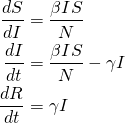Nas últimas semanas, o mundo foi assolado pela maior pandemia das últimas décadas, com impactos severos sobre os mercados globais e sobre os sistemas de saúde de grande parte dos países. No Brasil, o primeiro caso foi registrado no último dia 26 de fevereiro e a curva de crescimento dos infectados segue uma trajetória exponencial. De forma a compreender o comportamento dos casos no país, nós vamos implementar o famoso modelo SIR proposto por Kermack e McKendrick (1927) aos dados de covid-19 no Brasil. Meu objetivo aqui é basicamente construir o gráfico abaixo com as previsões de casos confirmados a partir de um modelo SIR.
require(nCov2019) require(dplyr) require(ggplot2) require(scales) require(gridExtra) require(deSolve)
Os dados são obtidos a seguir.
## Obtendo os dados data = load_nCov2019() data_global = data["global"] #extract global data data_br = filter(data_global, country == 'Brazil')
A seguir, visualizamos os dados.
Infected = data_br$cum_confirm Day <- 1:(length(Infected)) N <- 211289547 # População do Brasil df = tibble(Day, Infected, lnInfected = log(Infected)) g1 = ggplot(df, aes(x=Day, y=Infected))+ geom_line()+ geom_point()+ labs(x='Dias', y='Casos') g2 = ggplot(df, aes(x=Day, y=lnInfected))+ geom_line()+ geom_point()+ geom_smooth(method='lm', se=FALSE)+ labs(x='Dias', y='log(Casos)') grid.arrange(g1, g2, ncol=2, nrow=1, top='Total de Infectados por Covid-19 no Brasil')
O modelo SIR é um dos modelos epidemiológicos mais simples, e muitos modelos são derivações do mesmo. O modelo consiste em três compartimentos: S para o número de pessoas suscetíveis à doença, I para o número de infectados e R para o número de indivíduos recuperados (ou imunes).
Para modelar a dinâmica de uma epidemia, precisamos de três equações diferenciais, uma para a mudança em cada compartimento, com o parâmetro controlando a transição entre S e I e
controlando a transição entre I e R:
(1)
A seguir implementamos o código do blog Learning Machines para ajustar o modelo aos nossos dados:
SIR <- function(time, state, parameters) {
par <- as.list(c(state, parameters))
with(par, {
dS <- -beta/N * I * S
dI <- beta/N * I * S - gamma * I
dR <- gamma * I
list(c(dS, dI, dR))
})
}
init <- c(S = N-Infected[1], I = Infected[1], R = 0)
RSS <- function(parameters) {
names(parameters) <- c("beta", "gamma")
out <- ode(y = init, times = Day, func = SIR, parms = parameters)
fit <- out[ , 3]
sum((Infected - fit)^2)
}
Opt <- optim(c(0.5, 0.5), RSS,
method = "L-BFGS-B",
lower = c(0, 0), upper = c(1, 1))
Opt_par <- setNames(Opt$par, c("beta", "gamma"))
t <- 1:33 # time in days fit <- data.frame(ode(y = init, times = t, func = SIR, parms = Opt_par))
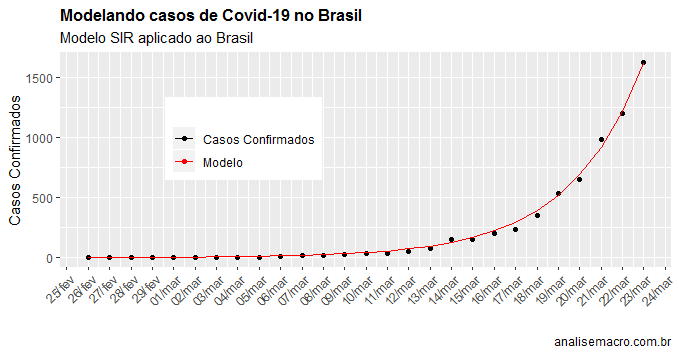
Com o modelo estimado, nós podemos ver o ajuste do mesmo abaixo.
df2 = tibble(time = data_br$time,
observado = data_br$cum_confirm,
modelo = round(fit$I[1:length(Infected)],0),
dias = Day)
ggplot(df2, aes(x=time))+
geom_point(aes(y=observado, colour='Casos Confirmados'),
stat='identity')+
geom_line(aes(y=modelo, colour='Modelo'))+
scale_colour_manual('',
values=c('Casos Confirmados'='black',
'Modelo'='red'))+
scale_x_date(breaks = date_breaks("1 day"),
labels = date_format("%d/%b"))+
theme(axis.text.x=element_text(angle=45, hjust=1),
plot.title = element_text(size=12, face='bold'),
legend.position = c(.3,.6))+
labs(x='', y='Casos Confirmados',
title='Modelando casos de Covid-19 no Brasil',
subtitle='Modelo SIR aplicado ao Brasil',
caption='analisemacro.com.br')
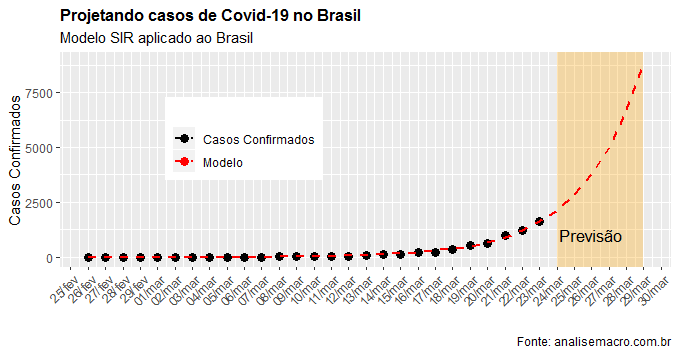
Na sequência nós visualizamos os casos previstos para os próximos dias.
dates = seq(data_br$time[1], length.out = length(t), by='1 days')
df3 = tibble(time = dates,
observado = c(data_br$cum_confirm,
rep(NA,
length(fit$I)-length(data_br$cum_confirm))),
modelo = round(fit$I,0))
ggplot(df3, aes(x=time))+
annotate("rect", fill = "orange", alpha = 0.3,
xmin = as.Date('2020-03-24'),
xmax = as.Date('2020-03-29'),
ymin = -Inf, ymax = Inf)+
annotate('text', x=as.Date('2020-03-26'), y=1000,
label='Previsão',
colour='black', size=4.5)+
geom_point(aes(y=observado, colour='Casos Confirmados'),
stat='identity', size=3)+
geom_line(aes(y=modelo, colour='Modelo'),
linetype='dashed', size=.8)+
scale_colour_manual('',
values=c('Casos Confirmados'='black',
'Modelo'='red'))+
scale_x_date(breaks = date_breaks("1 day"),
labels = date_format("%d/%b"))+
theme(axis.text.x=element_text(angle=45, hjust=1),
plot.title = element_text(size=12, face='bold'),
legend.position = c(.3,.6))+
labs(x='', y='Casos Confirmados',
title='Projetando casos de Covid-19 no Brasil',
subtitle='Modelo SIR aplicado ao Brasil',
caption='Fonte: analisemacro.com.br')
e
. Para os dados disponibilizados até aqui, a taxa de reprodução está em 1,79 no Brasil, abaixo de 2 que tem sido a taxa obtida em outros países.
________________________
Kermack, William Ogilvy, and Anderson G. McKendrick. 1927. “A Contribution to the Mathematical Theory of Epidemics.” Proceedings of the Royal Society of London, Series A 115, no. 772: 700–721.
(*) Aprenda R nos nossos Cursos Aplicados de R.
(**) Um pdf com os códigos estará disponível amanhã no Clube do Código.