No nosso Curso de Macroeconometria II, nós vemos diversas técnicas econométricas aplicadas a variáveis macroeconômicas reais. Para ilustrar, vamos considerar nesse comentário de conjuntura o comportamento da inércia inflacionária no período recente através da técnica de rolling regression. A abordagem de regressão recursiva é frequentemente usada na análise de séries temporais para avaliar a estabilidade dos parâmetros do modelo em relação ao tempo.
Para isso, vamos precisar carregar alguns pacotes e coletar o dado da inflação mensal diretamente do Banco Central com o pacote BETS. Você também pode usar outros pacotes para isso, como o rbcb ou o Quandl ou ainda a própria API do Banco Central.
library(BETS) library(lmtest) library(forecast) library(ggplot2) library(scales) ### Importando a inflação mensal ipca = BETSget(433, from='1999-06-01')
Eu peguei a inflação mensal a partir de junho de 1999, quando foi o publicado o decreto executivo sobre o regime de metas para inflação. Uma vez coletada a inflação, nós podemos construir nossa rolling regression. A ideia básica da regressão recursiva é tomar uma janela de observações e andar com ela ao longo da amostra disponível. Por exemplo, podemos criar uma janela com de 48 meses e estimar o nosso modelo para as primeiras 48 observações. Guardamos o parâmetro que interessa do modelo e andamos com a nossa janela, até chegar a última observação disponível.
Para fazer isso na prática, nós vamos precisar criar um loop, que basicamente automatiza o processo de andar com a nossa janela. Para não termos que repetir o processo acima n vezes.
Para fazer isso, primeiro, vamos setar algumas coisas, como o número de parâmetros a serem guardados e o tamanho da janela da rolling regression. Além disso, vamos criar matrizes para guardar os parâmetros estimados e os seus desvios-padrão.
### Criando matrizes que guardarão coeficientes e desvios-padrões
p <- 2 # Parâmetros a serem guardados
janela <- 48 # número de meses da janela
coefs <- matrix(NA, ncol = p, nrow = length(ipca)-janela)
dps <- matrix(NA, ncol = p, nrow = length(ipca)-janela)
colnames(coefs) <- c('AR(1)', 'Intercepto')
colnames(dps) <- c('AR(1)', 'Intercepto')
Uma vez que esteja tudo preparado para receber os valores, nós precisaremos estimar o nosso modelo. A ideia aqui é basicamente estimar um modelo AR(1), guardando assim o coeficiente autorregressivo que irá medir a inércia inflacionária ao longo do tempo.
### Loop para rodar o AR(1)
for (i in 1:nrow(coefs)){
ar1 <- Arima(ipca[(1+i-1):(janela+i-1)],
order=c(1,0,0))
coefs[i,] <- coef(ar1)
dps[i,] <- coeftest(ar1)[,2]
}
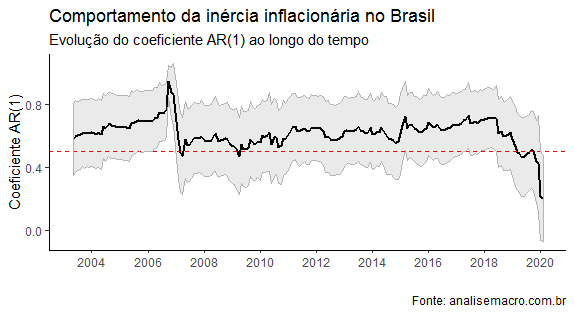
Uma vez estimado o modelo e guardado os parâmetros, nós podemos criar um gráfico como abaixo, que ilustrar o comportamento da inércia inflacionária ao longo do tempo. Isto é, o comportamento do coeficiente autorregressivo do nosso modelo AR(1).
Como se pode ver, há um recuo da inércia inflacionária a partir do início de 2018.
_____________________
(*) Isso e muito mais você irá aprender no nosso Curso de Macroeconometria II.