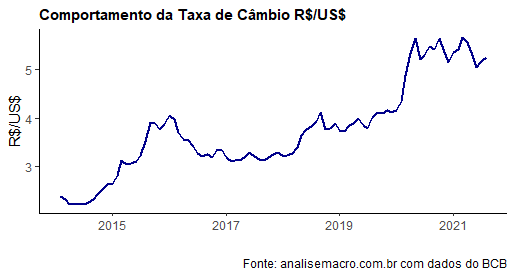
Uma piada bastante conhecida nas faculdades de economia é que Deus teria inventado o câmbio para humilhar os economistas. De fato, dada a enorme quantidade de fatores que o influenciam, é bastante desafiador tentar realizar alguma previsão decente dessa variável. Mas há algumas pistas, como exploramos nessa edição do Comentário de Conjuntura.
Os códigos dos nossos Comentários de Conjuntura são disponibilizados para os Membros do Clube AM. Conheça o Clube AM aqui.
Um modelo econométrico bastante utilizado para entender a trajetória da taxa de câmbio no Brasil foi proposto pelo Banco Central nos idos de 2001. O modelo era o seguinte:
(1)
onde:
é a taxa de câmbio;
é a taxa básica de juros do Br;
é a taxa básica de juros do US;
é uma medida de risco;
é a inflação do Br;
é a inflação do US.
Sobre a equação acima, por suposto, aplicamos a restrição de que , isto é, a variação do câmbio nominal, no equilíbrio, deve ser igual ao diferencial de inflação.
Nos últimos anos, a propósito, a previsão do câmbio tem sido ainda mais desafiador porque justamente uma das principais variáveis que interferem na sua trajetória é o ambiente político-econômico do país, que tem como proxy no modelo acima a medida de risco.
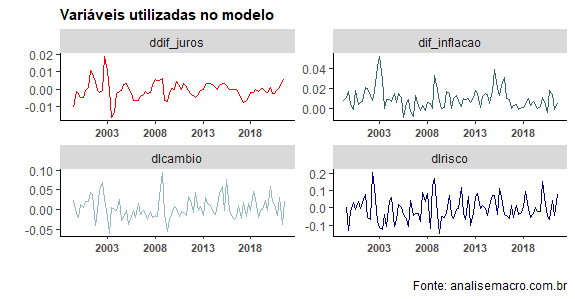
Para estimar esse modelo, nós baixamos os dados com o R do Banco Central, do FRED St Louis e do IpeaData. A coleta dos dados é seguida do seu tratamento, de modo a adequar os mesmos à estimação do modelo proposto acima. As variáveis ficam então apresentadas como no gráfico abaixo.
É esperado que o prêmio de risco tenha efeito positivo sobre o diferencial do câmbio, i.e., que cause desvalorizações cambiais enquanto o diferencial de juros exerceria pressão contrária. A tabela abaixo resume a estimação do modelo, com a imposição de restrição que fizemos.
| Estimate | Std. Error | t value | Pr(> | t| ) | |
| dlcambio_l1 | 0.560 | 0.063 | 8.818 | 0 |
| ddif_juros | -0.566 | 0.311 | -1.819 | 0.072 |
| dlrisco | 0.198 | 0.025 | 7.881 | 0 |
| dif_inflacao | 0.440 | 0.063 | 6.938 | 0 |
Os coeficientes estimados possuem os sinais esperados e apresentam significância estatística, com a imposição de restrição. O diferencial de juros aprecia a taxa de câmbio, enquanto o prêmio de risco tem efeito depreciativo.
Uma vez estimado o modelo e entendido a relação empírica entre as variáveis, o que podemos dizer sobre o período atual?
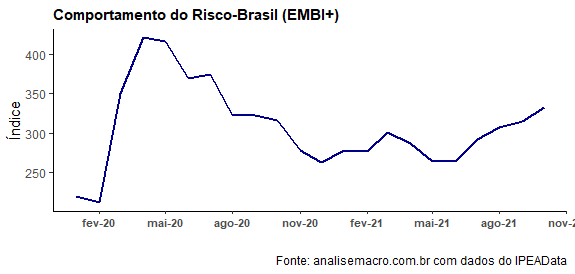
Por um lado, temos tido um aumento do risco-país, dada a deterioração do ambiente político-fiscal dos últimos meses. É esperado, inclusive, que essa deterioração continue no próximo ano, principalmente por causa das eleições.
Por outro lado, o aumento da taxa básica de juros, a Selic, em reação ao processo inflacionário descontrolado, tem tido influência sobre o diferencial de juros, o que em tese atrairia investimento em carteira para o Brasil e atenuaria essa pressão por desvalorização. Essas forças antagônicas dão o tom da trajetória do câmbio no curto prazo, gerando uma volatilidade bastante intensa.
Por óbvio, o modelo é simplificado ao ponto de não incluir outros atores importantes, em particular, a autoridade monetária, que pode (e deve?) intervir no mercado de modo a tentar suavizar esse aumento de volatilidade no curto prazo.
_______________________
(*) Para maiores detalhes sobre o uso desse tipo de modelo para fins de previsão, conheça nossos Cursos de Previsão Macroeconométrica e Modelos Preditivos aplicados à Macroeconomia.