O Hiato do produto é um indicador que visa medir as oscilações da economia, representando o quão distante ou próximo a economia está do seu potencial de crescimento. É possível realizar essa comparação por da diferença do PIB potencial com o PIB efetivo e no post de hoje, vamos mostrar os métodos utilizados para calcular o hiato do produto utilizando o R.
O que é Hiato do produto?
O PIB potencial é uma variável não observável, que mensura qual o potencial que um determinado pais pode produzir, isto é, caso não haja nenhuma ociosidade em seus fatores de produção. Por outro lado, o PIB efetivo é aquele que representa o valor histórico e ocorrido do PIB em um país.
O Hiato do produto surge da diferença entre o PIB Potencial e o PIB efetivo, e o seu conhecimento possibilita diversos benefícios.
Como medir o Hiato do produto?
Como dito, o Hiato do produto deve ser mensurado por meio da diferença entre o PIB Potencial e do PIB Efetivo, entretanto, é necessário obter formas de calcular o PIB Potencial. Entre as diversas formas, existem métodos estatísticos, que buscam analisar a tendencia da série do PIB, enquanto há uma abordagem econômica, por meio do calculo de uma função de produção.
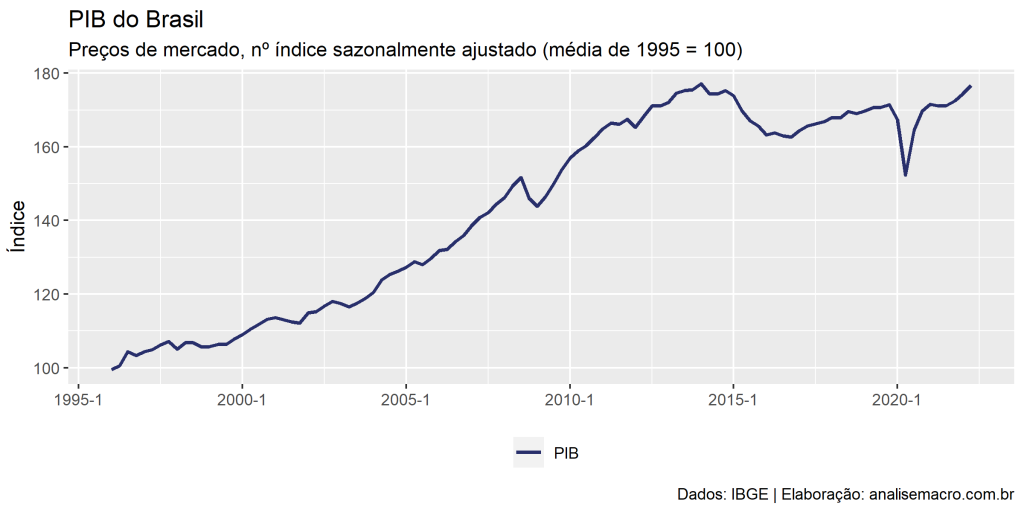
Primeiro, iremos importar os dados do PIB a preços de mercado, sazonalmente ajustado (PIB efetivo) para computar o PIB potencial, realizaremos isso utilizando o R.
</pre> library(tidyverse) library(zoo) pib <- sidrar::get_sidra(api = "/t/1621/n1/all/v/all/p/all/c11255/90707/d/v584%202") |> dplyr::mutate( data = zoo::as.yearqtr(`Trimestre (Código)`, format = "%Y%q"), tempo = dplyr::row_number() ) |> dplyr::select(data, "pib" = Valor) |> dplyr::as_tibble() # Gráfico de linha do PIB cores <- c( # vetor com códigos de cores "#282f6b", "#b22200", "#eace3f", "#224f20" ) g1 <- pib %>% # tabela de dados ggplot2::ggplot() + # camada inicial ggplot2::aes(x = data, y = pib, color = "PIB") + # especificação de eixos e título da série ggplot2::geom_line(size = 1) + # adiciona linha com observações ggplot2::scale_color_manual(values = cores) + # define cor da(s) linha(s) ggplot2::theme(legend.position = "bottom") + # posiciona a legenda embaixo ggplot2::labs( # textos de informação do gráfico title = "PIB do Brasil", subtitle = "Preços de mercado, nº índice sazonalmente ajustado (média de 1995 = 100)", y = "Índice", x = NULL, color = NULL, caption = "Dados: IBGE | Elaboração: analisemacro.com.br" ) g1 # plota o gráfico <pre>
Tendência
É possível estimar o PIB Potencial a partir da série do PIB efetivo calculando sua tendência por meio de uma regressão linear (MQO) . É possível usar uma tendência linear ou quadrática.
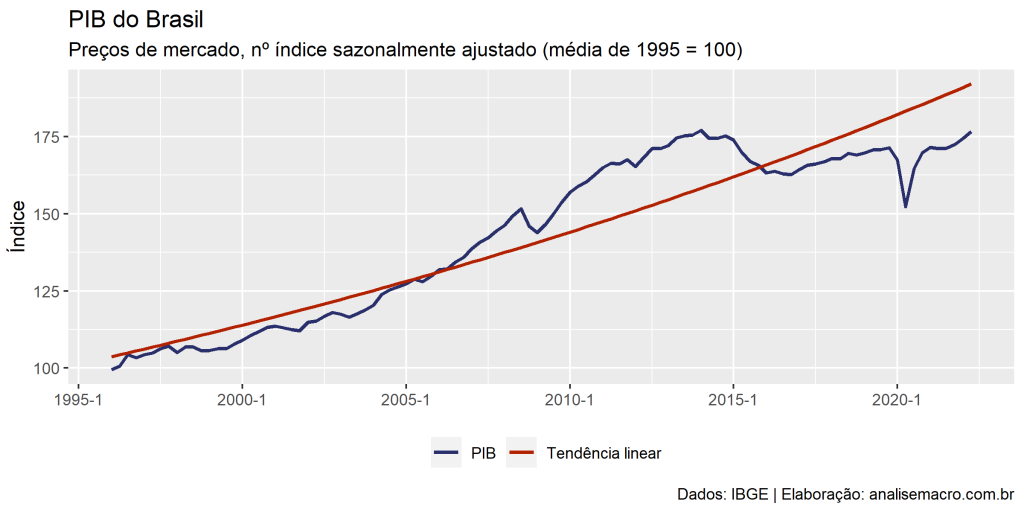
Tendência Linear
# Tendência linear -------------------------------------------------------- pib <- pib |> mutate( # Transformação logarítmica do PIB ln_pib = log(pib), # Vetor de 1 até T indicando ordenação temporal das observações tempo = dplyr::row_number() ) # Regressão linear do PIB contra o tempo reg1 <- lm( formula = ln_pib ~ tempo, # especificação do modelo no formato de fórmula data = pib # fonte dos dados ) # Salva a tendência estimada potencial_tl <- reg1 |> fitted() |> # extrai os valores estimados exp() # reverte a transformação logarítmica # Atualiza gráfico base com nova linha da tendência g1 + ggplot2::geom_line( mapping = ggplot2::aes(y = potencial_tl, color = "Tendência linear"), size = 1 )
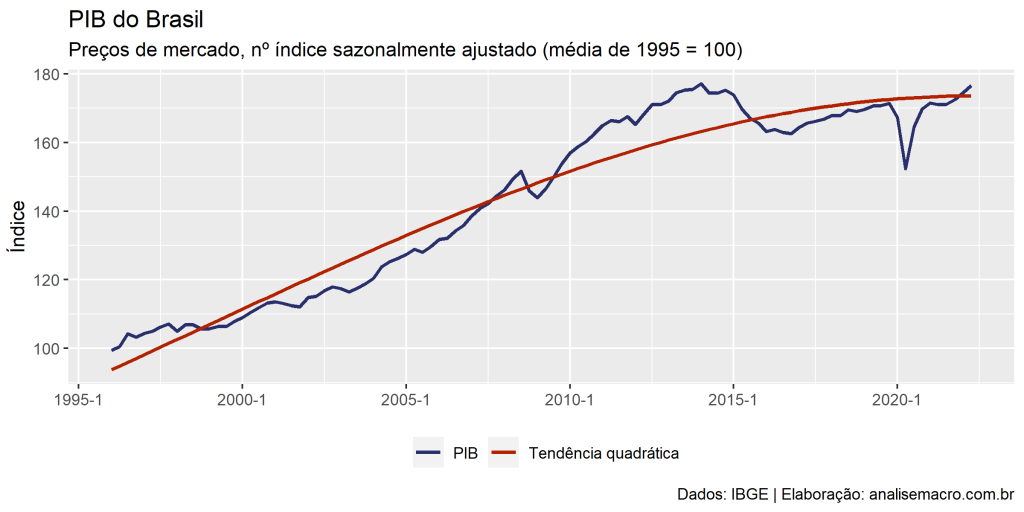
 Tendência quadrática
Tendência quadrática
</pre> # Tendência quadrática ---------------------------------------------------- # Regressão linear do PIB contra o tempo + tempo^2 (veja help de I) reg2 <- lm(formula = ln_pib ~ tempo + I(tempo^2), data = pib) # Salva a tendência estimada potencial_tq <- reg2 |> fitted() |> # extrai os valores estimados exp() # reverte a transformação logarítmica # Atualiza gráfico base com nova linha da tendência g1 + ggplot2::geom_line( mapping = ggplot2::aes(y = potencial_tq, color = "Tendência quadrática"), size = 1 ) <pre>
Filtro HP
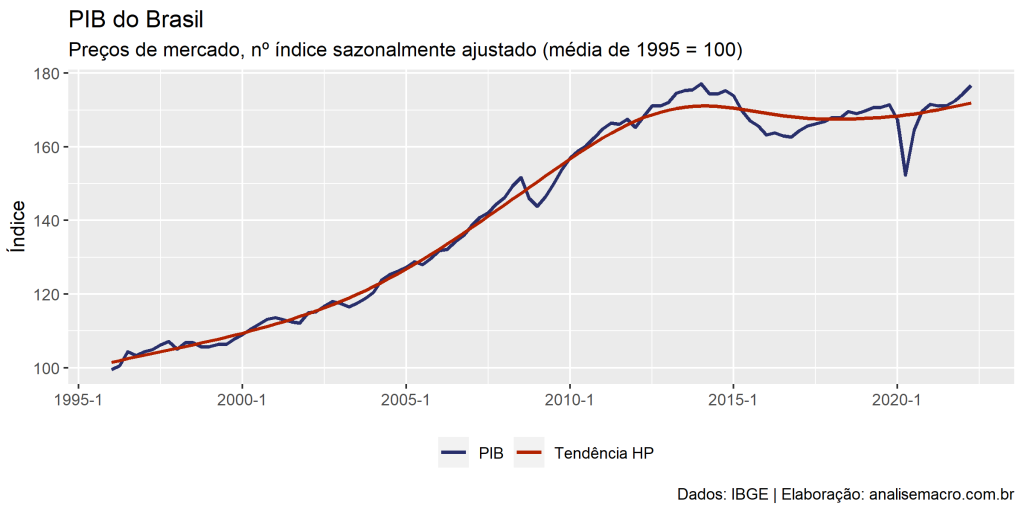
Hodrick–Prescott filter ou Hodrick–Prescott decomposition é um método matemático criado com o objetivo de servir de ferramenta de análise do ciclo econômico, possibilitando a decomposição de uma série temporal em elementos de tendência e ciclo.
O filtro HP separa uma série temporal em dois componentes: tendência (também chamado de crescimento) e ciclo. Dessa forma, Hodrick e Prescott (1997) propõem uma forma de criar uma equação, na qual isola-se o ciclo da série temporal e minimiza-se a tendência.
</span> # Filtro HP --------------------------------------------------------------- # Converte dados para classe ts dados_ts <- ts( # função para criar um objeto de classe ts data = pib$ln_pib, # vetor da série do PIB start = c( # vetor com dois elementos: ano e trimestre de início da série lubridate::year(min(pib$data)), # ano (formato AAAA) lubridate::quarter(min(pib$data)) # trimestre (formato T) ), frequency = 4 # frequência da série (trimestral = 4) ) # Calcula o filtro HP filtro_hp <- mFilter::hpfilter(x = dados_ts, type = "lambda", freq = 1600) # Salva a tendência calculada potencial_hp <- filtro_hp |> fitted() |> # extrai os valores estimados exp() |> # reverte a transformação logarítmica as.vector() # converte de classe ts para vetor numérico # Atualiza gráfico base com nova linha da tendência g1 + ggplot2::geom_line( mapping = ggplot2::aes(y = potencial_hp, color = "Tendência HP"), size = 1 ) <pre>
Filtro de Hamilton
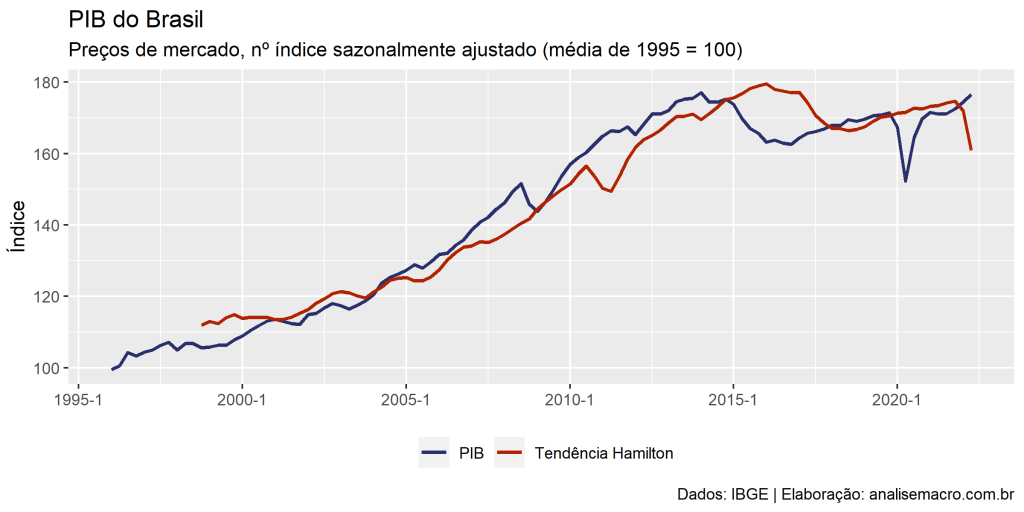
Este método é uma aplicação de uma especificação de um modelo de regressão linear (MQO) para extrair componentes de tendência e ciclo de uma série temporal, proposto por Hamilton (2017) como uma alternativa ao filtro HP.
</pre> # Filtro de Hamilton ------------------------------------------------------ # Regressão linear aplicando a especificação de Hamilton reg3 <- lm( formula = ln_pib ~ lag(ln_pib, 8) + lag(ln_pib, 9) + lag(ln_pib, 10) + lag(ln_pib, 11), data = pib, na.action = na.omit # omite os NAs criados pela função lag() ) # Salva a tendência estimada potencial_h <- reg3 |> fitted() |> # extrai os valores estimados exp() # reverte a transformação logarítmica # Adiciona 11 NAs no início da série para corresponder ao tamanho do vetor do PIB potencial_h <- c(rep(NA, 11), potencial_h) # Atualiza gráfico base com nova linha da tendência g1 + ggplot2::geom_line( mapping = ggplot2::aes(y = potencial_h, color = "Tendência Hamilton"), size = 1 ) <pre>
Cálculo do Hiato
Com o resultado de cada método proposto acima, podemos calcular o Hiato do produto por meio da diferença entre o PIB Potencial estimado em relação ao PIB Efetivo. Podemos ainda comparar em um gráfico a relação entre os valores obtidos de cada método por meio do código abaixo.
</pre>
# Calculando o hiato ------------------------------------------------------
# Cálculo do hiato do produto
hiato <- pib |>
dplyr::select("data", "pib") |> # seleciona colunas de interesse
dplyr::mutate( # cria novas colunas com cálculo do hiato
`Tendência Linear` = (pib / potencial_tl - 1) * 100,
`Tendência Quadrática` = (pib / potencial_tq - 1) * 100,
`Filtro HP` = (pib / potencial_hp - 1) * 100,
`Filtro de Hamilton` = (pib / potencial_h - 1) * 100
) |>
tidyr::pivot_longer( # transforma a tabela pro formato "longo" (mais linhas e menos colunas)
cols = 3:6, # colunas a serem transformadas
names_to = "variavel", # nome da coluna que armazenará os nomes das colunas 3:6
values_to = "valor" # nome da coluna que armazenará os valores das colunas 3:6
)
# Visualização de dados: gráfico de linha dos hiatos estimados
hiato |>
ggplot2::ggplot() +
ggplot2::aes(x = data, y = valor, color = variavel) +
ggplot2::geom_hline(yintercept = 0, linetype = "dashed") + # gera uma linha horizontal quando y = 0
ggplot2::geom_line(size = 1) +
ggplot2::scale_color_manual(values = cores) +
ggplot2::theme(legend.position = "top") +
ggplot2::labs(
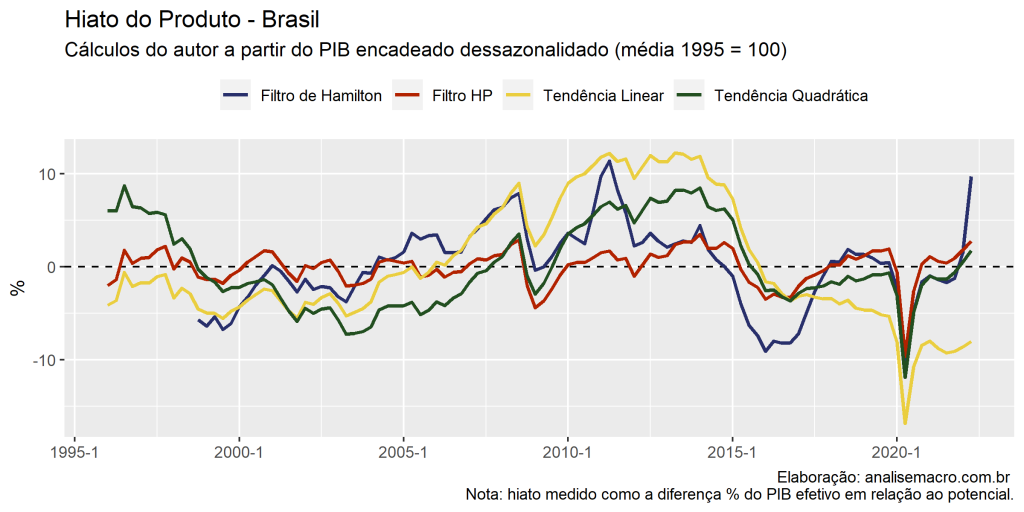
title = "Hiato do Produto - Brasil",
subtitle = "Cálculos do autor a partir do PIB encadeado dessazonalidado (média 1995 = 100)",
y = "%",
x = NULL,
color = NULL,
caption = "Elaboração: analisemacro.com.br \n Nota: hiato medido como a diferença % do PIB efetivo em relação ao potencial."
)
_____________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia