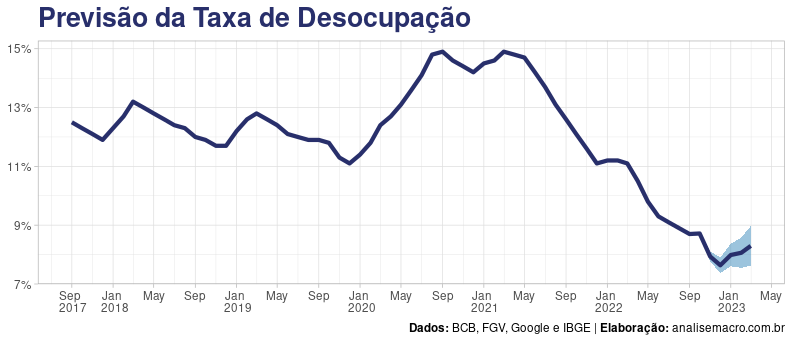
O objetivo do post de hoje será criar um modelo de previsão do Desemprego medido pela PNAD por meio de um Modelo Vetorial de Correção de Erros (VEC).
Regressão e relações espúrias
Um problema comum do uso do modelo de regressão linear em séries temporais está no fato de que determinadas séries, principalmente econômicas, podem apresentar resultados inconsistentes, devido a suposições do MQO em relação as propriedades estatísticas das variáveis, tais como a média condicional e a variância condicional, de séries econômicas que oscilam ao longo do tempo. Caso haja esse relação, e as séries exibam tendências, é possível o aparecimento do que chama-se de regressão espúria, isto é, variáveis que apesar de possuírem forte relação estatística por meio da regressão linear, só as possuem devido a essa tendência comum.
Cointegração
Um exceção a isso vem caso as variáveis compartilhem a mesma tendencia estocástica, possibilitando o uso de outros tipos de modelos. Para ilustrar, considere, duas séries integradas de ordem 1, e
, e suponha que exista uma relação linear entre elas, dada por
. Isso implica no fato de existir algum valor de
tal que
seja integrado de ordem zero, mesmo com as séries originais sendo ambas não estacionárias. Nesses casos, diz-se que as séries são cointegradas e as mesmas compartilham a mesma tendência.
A ideia por trás da cointegração é que variáveis não estacionárias podem possuir uma trajetória temporal interligada, representando que haja uma tendência estocástica entre as séries. Isso possibilita a construção de um modelo que descreve as relações de equilíbrio de longo prazo entre as variáveis.
Cointegração e VECM
O Modelo Vetorial de Correção de Erros (VEC) utiliza a análise de cointegração para a estimação de modelos que descrevem os co-movimentos dinâmicos de duas ou mais séries temporais. Portanto, podemos definir que quando é
, dizemos que
e
são cointegradas, pois possuem trajetórias temporais interligadas de forma que no longo prazo apresentam relação de equilíbrio. Entretanto, $a_t$ é variante no tempo, representando os desvios de curto prazo dessa relação de equilíbrio e sendo chamada de erro de equilíbrio.
O modelo de correção de erros visa ajustar esses desequilíbrio de curto prazo e nos permite obter a taxa no qual o sistema retorna ao equilíbrio após os desvios. O Modelo Vetorial de Correção de Erros (VEC) é um VAR que possui restrições de cointegração e o termo da cointegração no VAR é o termo de correção de erros.
Previsão do Desemprego
Após essa breve introdução sobre o modelo escolhido, vamos definir os passos do processo de análise de dados e os passos que seguiremos para criar o modelo. Seguiremos os seguintes passos no R:
- Coleta
- Tratamento
- Visualização
- Modelagem
- Previsão/Visualização
Para a coleta, utilizaremos os seguintes dados para o modelo
- Taxa de desocupação, na semana de referência, das pessoas de 14 anos ou mais de idade - SIDRA;
- Indicador Antecedente de Emprego (IAEmp) com ajuste sazonal - FGV;
- Indicador de Incerteza da Economia Brasil (IIE-Br) - FGV;
- Termos de busca: "empregos" e "seguro desemprego no Google Trends - Google;
- Índice de Atividade Econômica do Banco Central (IBC-Br) com ajuste sazonal - BCB;
- Taxa de juros Selic acumulada no mês anualizada base 252 - BCB.
Todas as variáveis acima, exceto as FGV foram coletadas de forma automática com o R. Os dados da FGV foram importados de forma manual, através do download do arquivo .xls das séries escolhidas.
Em relação a Modelagem, por utilizarmos um modelo VEC, seguiremos os seguintes passos:
- Teste de estacionariedade das séries para certificar que são candidatas a cointegração;
- Teste de cointegração de Johansen para certificar que as séries são cointegradas;
- Transformar o modelo VEC em VAR;
- Realizar a previsão fora da amostra
Vamos então aos procedimentos com o R.
Exemplo com o R
Pacotes e utilidades
# Carregar pacotes library(sidrar) library(gtrendsR) library(GetBCBData) library(readxl) library(dplyr) library(magrittr) library(tibble) library(purrr) library(lubridate) library(ggplot2) library(scales) library(ggtext) library(urca) library(vars) library(forecast) library(stringr) library(tidyr) # Cores para gráficos colors <- c( blue = "#282f6b", red = "#b22200", yellow = "#eace3f", green = "#224f20", purple = "#5f487c", orange = "#b35c1e", turquoise = "#419391", green_two = "#839c56", light_blue = "#3b89bc", gray = "#666666" )
Coleta
# Coleta -----------------------
# Dados do Sidra/IBGE
dados_sidra <- sidrar::get_sidra(
api = "/t/6381/n1/all/v/4099/p/all/d/v4099%201"
)
# Dados da FGV (salvos na pasta data)
dados_fgv <- readxl::read_xls(
path = "xgvxConsulta.xls",
col_types = c("text", "numeric", "numeric"),
skip = 15,
na = "-",
col_names = c("date", "iaemp", "iie")
)
# Dados do Google Trends
dados_google <- gtrendsR::gtrends(
keyword = c("empregos", "seguro desemprego"),
geo = "BR",
time = "all",
onlyInterest = TRUE
)
# Dados do BCB
dados_bcb <- GetBCBData::gbcbd_get_series(
id = c("ibc" = 24364, "selic" = 4189),
first.date = "2012-03-01",
format.data = "wide",
use.memoise = FALSE
)
Tratamento
# Tratamento ------------------------------
# Dados em formato data.frame
dados <- purrr::reduce(
.x = list(
# Taxa de desocupação
"sidra" = dados_sidra %>%
dplyr::select(
"date" = "Trimestre M\u00f3vel (C\u00f3digo)",
"desocupacao" = "Valor"
) %>%
dplyr::mutate(date = lubridate::ym(.data$date)),
# Selic e IBC-Br
"bcb" = dados_bcb %>%
dplyr::rename("date" = "ref.date"),
# Google Trends "empregos"
"google" = dados_google %>%
magrittr::extract2(1) %>%
dplyr::select("date", "gtrends" = "hits", "variable" = "keyword") %>%
dplyr::mutate(date = lubridate::as_date(.data$date)) %>%
dplyr::filter(.data$date >= lubridate::as_date("2012-03-01", format = "%Y-%m-%d")) %>%
tidyr::pivot_wider(
id_cols = .data$date,
names_from = .data$variable,
values_from = .data$gtrends
),
# IAEmp e IIE-Br
"fgv" = dados_fgv %>%
dplyr::mutate(
date = paste0("01/", .data$date) %>% lubridate::dmy()
) %>%
dplyr::filter(.data$date >= lubridate::as_date("2012-03-01", format = "%Y-%m-%d"))
),
.f = dplyr::full_join,
by = "date"
) %>%
tidyr::drop_na()
# Dados em formato time series
dados_ts <- stats::ts(
data = dados[-1],
start = c(
lubridate::year(min(dados$date)),
lubridate::month(min(dados$date))
),
frequency = 12
)
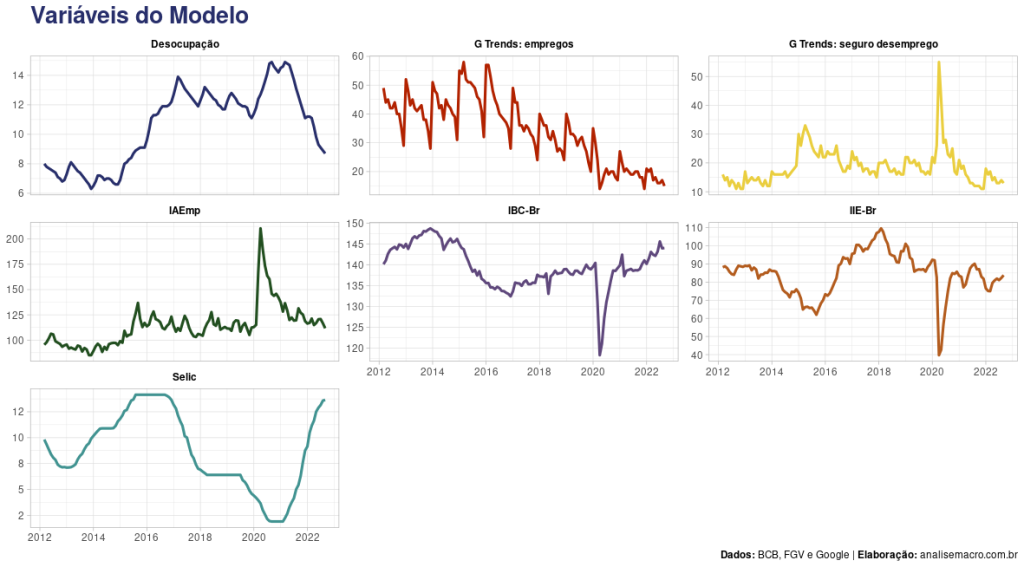
Visualização das variáveis
# Visualização --------------------------------------
dados %>%
dplyr::rename_with(
~c("date",
"Desocupação",
"IBC-Br",
"Selic",
"G Trends: empregos",
"G Trends: seguro desemprego",
"IAEmp",
"IIE-Br")
) %>%
tidyr::pivot_longer(cols = -.data$date, names_to = "variable", values_to = "value") %>%
ggplot2::ggplot(ggplot2::aes(x = .data$date, y = .data$value, colour = .data$variable)) +
ggplot2::geom_line(size = 1.1) +
ggplot2::theme_light() +
ggplot2::scale_colour_manual(NULL, values = unname(colors)) +
ggplot2::scale_y_continuous(
breaks = scales::breaks_extended(7),
labels = scales::number_format(accuracy = 1)
) +
ggplot2::facet_wrap(~variable, scales = "free_y") +
ggplot2::labs(
title = "**Variáveis do Modelo**",
y = NULL,
x = NULL,
caption = "**Dados:** BCB, FGV e Google | **Elabora\u00e7\u00e3o:** analisemacro.com.br"
) +
ggplot2::theme(
plot.title = ggtext::element_markdown(size = 20, colour = colors[1]),
plot.caption = ggtext::element_markdown(),
legend.position = "none",
strip.background = ggplot2::element_rect(fill = "transparent"),
strip.text = ggtext::element_markdown(face = "bold", colour = "black")
)
Modelagem
Testes de estacionariedade
# Teste de Estacionariedade ---------
# Teste de ADF de raíz unitária
# Objeto auxiliar com nomes das variáveis/tipo de teste ADF
adf_names <- list(
names(dados[-1]),
c("none", "drift", "trend")
) %>%
purrr::cross() %>%
purrr::map(purrr::lift(paste, sep = "/"))
# Implementar teste ADF
adf_test <- list(
purrr::map(as.list(dados[-1]), ~.x[!is.na(.x)]), # variáveis
c("none", "drift", "trend") # tipo do teste
) %>%
purrr::cross() %>%
purrr::set_names(adf_names) %>%
purrr::map(
~urca::ur.df(y = .[[1]], type = .[[2]], lags = 12) # teste
) %>%
purrr::map2(
.x = .,
.y = adf_names,
~{.x@test.name = .y; return(.x)}
)
Teste de Cointegração
# Teste de cointegração -------------------------------
# Setar semente
set.seed(1984)
# Seleção de defasagens VAR
var_lags <- vars::VARselect(
y = dados_ts,
lag.max = 36, # número de defasagens máximo
type = "both", # incluir constante e tendência
season = 12 # incluir dummies sazonais
) %>%
magrittr::extract2("selection") %>%
table() %>%
sort(decreasing = TRUE) %>%
magrittr::extract(1) %>%
names() %>%
as.numeric()
# Teste de cointegração de Johansen/VECM
johansen_vecm <- urca::ca.jo(
x = dados[-1],
type = "trace", # teste do traço
ecdet = "const", # adicionar constante
K = var_lags, # número de defasagens máximo
spec = "transitory", # especificação VECM
season = 12 # incluir dummies sazonais
)
Previsão do Modelo
# VECM: previsão fora da amostra ------------------
# Transformar VECM para VAR em nível
modelo_var <- vars::vec2var(johansen_vecm, r = 5)
# Previsões fora da amostra
previsao_oos <- predict(
object = modelo_var,
n.ahead = 6
) %>%
magrittr::extract2("fcst") %>%
magrittr::extract2("desocupacao") %>%
dplyr::as_tibble() %>%
dplyr::mutate(
"date" = seq.Date(
from = dplyr::last(dados$date) %m+% months(1),
by = "month",
length.out = nrow(.)
),
"id" = "Previs\u00e3o"
) %>%
dplyr::rename("value" = "fcst")
# Gráfico
plt_previsao <- dados %>%
dplyr::filter(.data$date >= max(.data$date) %m-% lubridate::years(5)) %>%
dplyr::select(.data$date, "value" = .data$desocupacao) %>%
dplyr::mutate("id" = "Taxa de Desocupa\u00e7\u00e3o") %>%
dplyr::full_join(
previsao_oos,
by = c("date", "value", "id")
) %>%
ggplot2::ggplot(ggplot2::aes(x = .data$date, y = .data$value)) +
ggplot2::geom_ribbon(
ggplot2::aes(ymin = .data$lower, ymax = .data$upper),
fill = colors["light_blue"],
alpha = 0.5
) +
ggplot2::geom_line(size = 1.5, colour = colors[1]) +
ggplot2::theme_light() +
ggplot2::scale_y_continuous(
labels = scales::number_format(suffix = "%", accuracy = 1)
) +
ggplot2::scale_x_date(
breaks = scales::breaks_width("4 months"),
labels = function(x) dplyr::if_else(
is.na(dplyr::lag(x)) | !lubridate::year(dplyr::lag(x)) == lubridate::year(x),
paste(lubridate::month(x, label = TRUE), "\n", lubridate::year(x)),
paste(lubridate::month(x, label = TRUE))
)
) +
ggplot2::labs(
title = "**Previs\u00e3o da Taxa de Desocupa\u00e7\u00e3o**",
y = NULL,
x = NULL,
caption = "**Dados:** BCB, FGV, Google e IBGE | **Elabora\u00e7\u00e3o:** analisemacro.com.br"
) +
ggplot2::theme(
plot.title = ggtext::element_markdown(size = 20, colour = colors[1]),
plot.caption = ggtext::element_markdown()
)
_____________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia