[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="left" use_border_color="off" border_color="#ffffff" border_style="solid"]
Na edição 13 do Clube do Código, apresentamos um modelo SARIMA para a inflação medida pelo IPCA. Hoje, vamos extender esse modelo com a inclusão de algumas variáveis, o que dá origem a um modelo SARIMAX. Os dados estão no arquivo data.csv e são importados para o R abaixo.
data = ts(read.csv2('data.csv', header=T, dec=',', sep=';')[,-1], start=c(2001,11), freq=12)
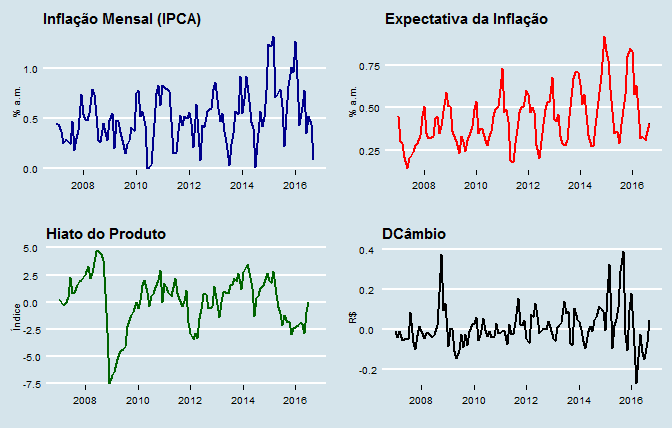
Antes de visualizar os dados, precisamos criar o hiato do produto. Isso é feito abaixo, com a função hpfilter do pacote mFilter.
[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/11/macroeconometria.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/macroeconometria/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="left" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="Linha"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="left" use_border_color="off" border_color="#ffffff" border_style="solid"]
pib.hp = hpfilter(na.omit(data[,3]), type='lambda', freq=14400)
data = cbind(data[,c(1,2)], pib.hp$cycle, diff(data[,4]))
colnames(data) = c('ipca', 'expectativa', 'hiato', 'dcambio')
Agora, assim, podemos ver os gráficos.
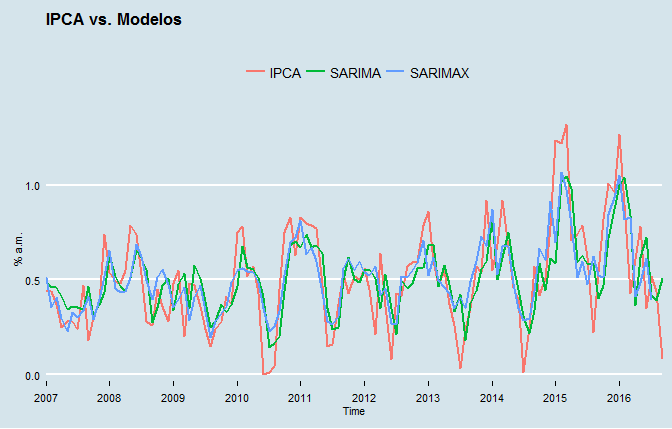
Para criar o modelo SARIMAX, vamos utilizar a base do modelo SARIMA que estimamos naquela edição. Com essa base, nós podemos adicionar nossos regressores adicionais. Ademais, para fins de comparação, vamos estimar o mesmo SARIMA. Uma vez feito isso, colocamos os modelos abaixo.
Agora, antes de gerarmos previsões, precisamos completar os missing values no hiato do produto. Isso é feito abaixo.
hiato.forecast = forecast(auto.arima(data[,3], max.p=4, max.q=4, seasonal = F), h=17, level=40) data[c(nrow(data),nrow(data)-1),3] = hiato.forecast$mean[1:2]
Agora, podemos organizar os cenários.
### Cenário Base
cen.base = ts(read.csv2('cenarios.csv', header=T, sep=';', dec=',')[,2:3], start=c(2016,10), freq=12)
cen.base = cbind(cen.base[,1], hiato.forecast$mean[3:17], cen.base[,2])
colnames(cen.base) = c('expectativa', 'hiato', 'dcambio')
### Cenário Pessimista
cen.pessim = ts(read.csv2('cenarios.csv', header=T, sep=';', dec=',')[,4:5], start=c(2016,10), freq=12)
cen.pessim = cbind(cen.pessim[,1], hiato.forecast$upper[3:17], cen.pessim[,2])
colnames(cen.pessim) = c('expectativa', 'hiato', 'dcambio')
### Cenário Otimista
cen.otim = ts(read.csv2('cenarios.csv', header=T, sep=';', dec=',')[,6:7], start=c(2016,10), freq=12)
cen.otim = cbind(cen.otim[,1], hiato.forecast$lower[3:17], cen.otim[,2])
colnames(cen.otim) = c('expectativa', 'hiato', 'dcambio')
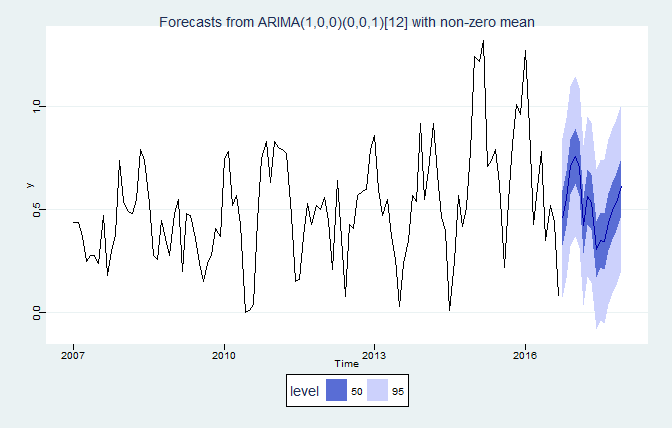
Uma vez feito isso, podemos utilizar o pacote forecast para gerar as previsões. As previsões utilizadas com o cenário base são postas abaixo.
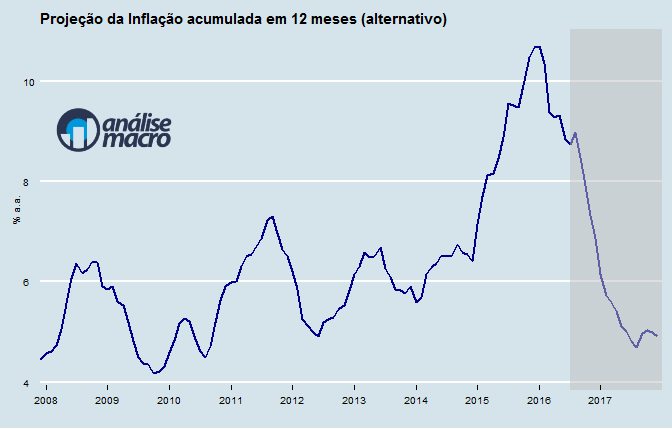
Com os resultados, construímos também um cenário alternativo para a inflação acumulada em 12 meses. A trajetória de desinflação esperada é posta abaixo.
[/et_pb_text][et_pb_button admin_label="Botão" button_url="https://analisemacro.com.br/cursos-de-r/macroeconometria/" url_new_window="off" button_text="Curso de Macroeconometria usando o R" button_alignment="center" background_layout="light" custom_button="off" button_letter_spacing="0" button_use_icon="default" button_icon_placement="right" button_on_hover="on" button_letter_spacing_hover="0"] [/et_pb_button][/et_pb_column][/et_pb_row][/et_pb_section]