[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]
Desde o ano passado, os economistas brasileiros estão orfãos da Pesquisa Mensal de Emprego do IBGE. Em seu lugar, o instituto tem divulgado mensalmente a PNAD Contínua com base em trimestres móveis. O problema nessa mudança é que a série da PNAD é curta, o que impede esses mesmos economistas de fazer algum exercício mais sofisticado com os dados. Esse, a propósito, é um dos problemas que temos ajudado a resolver com os cursos aplicados da Análise Macro. Vamos mostrar aqui como podemos usar o R para estender a amostra da taxa de desemprego da PNAD com base na taxa de desemprego da PME, tendo assim uma série com mais observações.
Abaixo levamos os dados para o R:
library(BETS)
pme = ts(read.csv2('pme.csv', header=T, sep=';', dec=',')[,-1],
start=c(2002,03), freq=12)
pnad = BETS.get(24369)
data = cbind(pme,pnad)
Uma vez importados os dados, observamos como esperado que as mesmas possuem tamanhos diferentes. Um primeiro ajuste, portanto, é igualar a amostra das séries. Isso é feito abaixo.
desemprego = ts(data[complete.cases(data),], start=c(2012,03), freq=12)
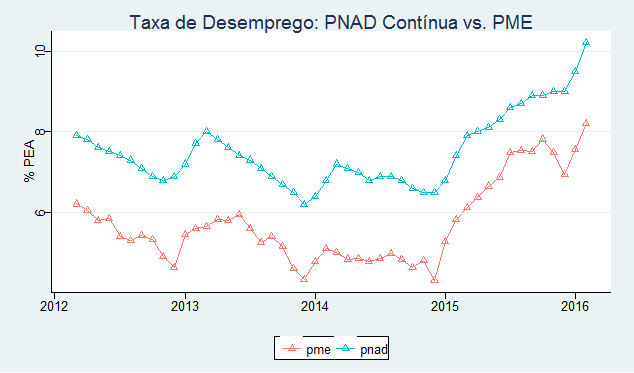
Abaixo um gráfico com as séries.
O gráfico nos mostra que a série da PNAD Contínua tem uma média maior do que a da PME. Ambas as séries caminham, entretanto, de forma parecida, a despeito da diferença da amostra. Abaixo as estatísticas descritivas das duas séries.
| Statistic | N | Mean | St. Dev. | Min | Max |
| pme | 48 | 5,73 | 1,01 | 4,30 | 8,20 |
| pnad | 48 | 7,51 | 0,89 | 6,20 | 10,20 |
Uma vez definido o conjunto de dados, passemos ao exercício em si. Como o nosso objetivo é basicamente expandir a taxa de desemprego da PNAD Contínua, vamos então regredir a mesma contra a taxa da PME.
reg = lm(pnad~pme, data=desemprego)
A tabela 2 resume a regressão.
| Dependent variable: | |
| pnad | |
| pme | 0.842*** |
| (0.037) | |
| Constant | 2.682*** |
| (0.213) | |
| Observations | 48 |
| R2 | 0.920 |
| Adjusted R2 | 0.919 |
| Residual Std. Error | 0.253 (df = 46) |
| F Statistic | 531.093*** (df = 1; 46) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
Em outras palavras, a taxa de desemprego da PNAD estimada e a da PME se relacionam pela equação
(1)
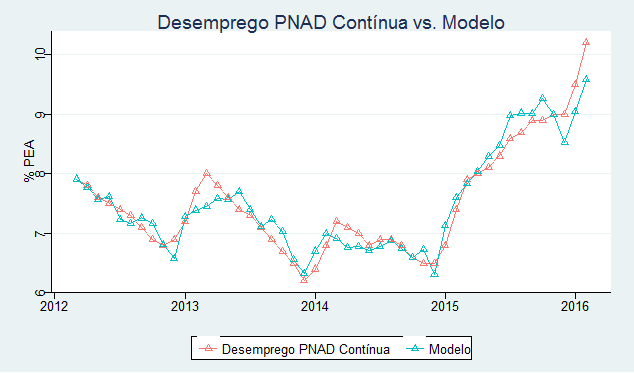
Abaixo, plotamos a série original da taxa de desemprego da PNAD Contínua contra a taxa gerada pelo modelo.
Uma vez estimado o modelo, podemos agora utilizá-lo para construir nossa série de desemprego da PNAD Contínua para trás, com base na taxa de desemprego da PME. Isso é feito com o código abaixo.
### Criar Série PNAD Contínua Ampliada pnad.pme = ts(data[!complete.cases(data[,2]),], start=c(2002,03), freq=12) pnad.pme[,2] = coef(reg)[1] +coef(reg)[2]*pnad.pme[,1] data[1:nrow(pnad.pme),2] = pnad.pme[1:nrow(pnad.pme),2] pnad = data[,2]
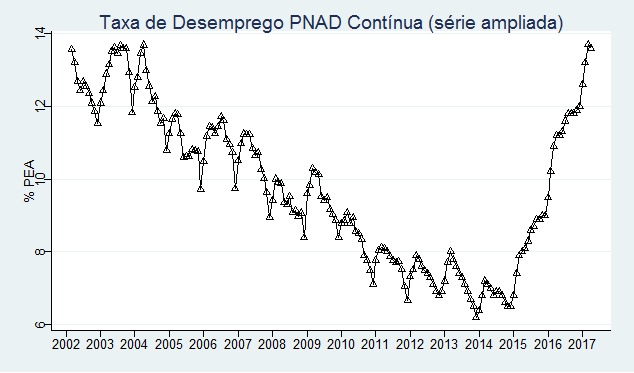
E agora a taxa de desemprego que construímos.
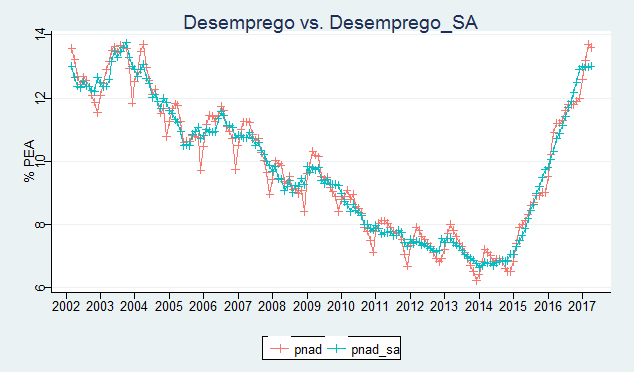
Podemos, agora, dessazonalizar a nossa taxa de desemprego, utilizando o pacote seasonal e colocar abaixo as duas séries.
Temos agora duas séries, uma normal e outra dessazonalizada, que podemos utilizar em exercícios futuros. Observe, entretanto, que a mesma é apenas uma aproximação estatística da PNAD Contínua através da PME, ok? Até o próximo exercício e não esqueça de dar uma olhada nos cursos aplicados de R da Análise Macro! 🙂
[/et_pb_text][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2017/06/fb.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/macroeconomia-aplicada" url_new_window="off" use_overlay="off" animation="off" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"] [/et_pb_image][/et_pb_column][/et_pb_row][/et_pb_section]