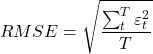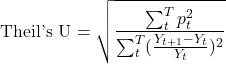Introdução

Vimos uma introdução à estratégias de previsão macroeconométrica, que elenca as seguintes etapas:

• Definição do problema
• Coleta dos Dados
• Análise dos Dados
• Identificação do modelo e estimação
• Diagnóstico dos modelos estimados
• Implantação do modelo de previsão
• Avaliação do modelo de previsão

Uma extensão natural a esse tipo de trabalho é, certamente, avaliar o quão bom ou ruim é a previsão gerada. Para tanto, vamos entender quais os conceitos, a estratégia e como avaliar as previsões que desejamos realizar.

Previsões

Após as etapas de estimação e diagnóstico dos modelos estimados, encontramos um modelo candidato, o próximo passo é avaliar a qualidade das previsões geradas pelo modelo. E por previsões vale distinguir os dois tipos:

Após as etapas de estimação e diagnóstico dos modelos estimados, encontramos um modelo candidato, o próximo passo é avaliar a qualidade das previsões geradas pelo modelo. E por previsões vale distinguir os dois tipos:

• Previsão estática: usa na previsão de o valor de . Também
  chamada de previsão um passo à frente, pois atualiza o valor da série até o período anterior para fazer a próxima previsão (útil para verificar o ajustamento do modelo).
• Previsão dinâmica: não usa a informação adicional para realimentar as previsões. Isto é, para prever , usa-se .

Uma boa estratégia para avaliar as previsões de um modelo de séries temporais é:

1. Restringir a amostra de dados, omitindo um horizonte de observações, geralmente do final da amostra;
2. Estimar o modelo com a amostra restringida e gerar previsão dinâmica ℎ passos a frente, conhecida como previsão pseudo out-of-sample;
3. Calcular o erro de previsão , ou seja, os valores observados (que ficaram omitidos na estimação) menos o que foi previsto “fora da amostra” pelo modelo;
4. Calcular métricas de acurácia (ME, MSE, RMSE, MAE, MPE, MAPE, U de Theil, etc.) para comparar a previsão entre modelos;
5. Escolher o modelo que apresenta a melhor (menor) métrica de acurácia. Em geral, utiliza-se o RMSE para decidir entre modelos.

Cenários e variáveis exógenas

Note que, para o caso de modelos multivariados, você precisará dos valores futuros das variáveis independentes para poder gerar previsões para a variável dependente. Ou seja, você precisa informar uma matriz com os ℎ valores futuros das variáveis independentes no momento da previsão. Nos demais casos, modelos univariados e modelos multivariados endógenos, não há tal necessidade, a menos que contenham variáveis exógenas como dummies sazonais (nesse caso, informe uma matriz de dummies sazonais com ℎ linhas).

Para quando isso é necessário, há múltiplas possibilidades: você pode simplesmente calcular a média histórica e usar esses valores na previsão; informar valores com base em previsões externas (Focus, por exemplo); informar valores com base em leitura da conjuntura econômica (com algum viés e arbitrariedade); etc.

Por fim, uma vez que você tenha um modelo candidato com boa performance em previsões, você pode usar a amostra completa de dados para gerar previsões fora da amostra.

Definindo as métricas

A primeira consiste simplesmente na média da série de erros de previsão, isto é, o erro médio (ME), dado conforme segue:

(1)  

A segunda é a raiz quadrada do erro médio (RMSE), dada por

(2)  

A terceira medida, por sua vez, é dada pela média dos erros em valores absolutos ou simplesmente erro médio absoluto (MAE), expressa conforme

(3)  

Essas três medidas fazem parte do grupo de medidas que dependem da escala na qual os dados estão. Logo, elas podem ser utilizadas para efeito de comparação de diferentes modelos aplicados a mesma amostra de dados.

A quarta medida é o erro médio percentual (MPE), isto é,

(4)  

A quinta medida é o **erro médio absoluto percentual** (MAPE), dado conforme

(5)  

Por se tratarem de percentuais, essas medidas não são sensíveis à escala dos dados.

A sexta medida fornecida é a ACF1, isto é, o coeficiente de autocorrelação parcial de primeira ordem. Ele nos dá uma ideia de existência de estrutura nos erros de previsão, que, por suposição, deveriam ser um **ruído branco**. Quanto maior esta medida, maior será o indicio de existência de estrutura.

Por fim, temos o U de Theil dado por

(6)  

Essa medida pertence à categoria de medidas relativas. Será dada pela razão entre a raiz quadrada da média do erro percentual quadrático e a raiz quadrada da média da taxa de variação percentual quadrática da série observada.

Em outros termos, o U de Theil nada mais é do que a comparação entre o modelo em questão e um simples passeio aleatório. Quanto menor o índice, portanto, melhor será o modelo, se comparado a um passeio aleatório.

___________________________________
Quer aprender mais?

Seja um aluno da nossa trilha de Macroeconomia Aplicada  e aprenda a criar projetos voltados para a Macroeconomia.

Referências