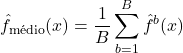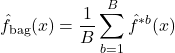Bagging, Random Forests e Boosting

Nesse artigo, vamos ilustrar os métodos Bagging, Random Forests e Boosting usando árvores de decisão como blocos de construção para construir modelos de previsão mais poderosos.

Bagging

A técnica de bootstrap que vimos anteriormente pode ser extremamente útil para o cálculo de desvio-padrão em situações onde isso pode não ser possível. Já aqui, vamos ver o emprego dessa técnica com o intuito de aumentar a performance de métodos de aprendizado como as àrvores de decisão.

Àrvores de decisão têm alta variância. Isso significa que se, por exemplo, dividirmos o conjunto de treino em duas partes e rodarmos nosso modelo em ambas, os resultados podem ser bastante diferentes.

Procedimentos com baixa variância, por outro lado, levariam a resultados similares nesse contexto.

Por exemplo, regressões lineares com $n$ e $p$ moderadamente grandes são modelos com baixa variância e, consequentemente, com resultados similares para diferentes conjuntos de dados.

Nesse sentido, a técnica de Bootstrap aggregation ou simplesmente Bagging é um procedimento de propósito geral que possibilita justamente a redução de variância de diferentes métodos de aprendizado.

Vamos introduzir o método no contexto de arvores de decisão, mas o mesmo pode ser utilizado, como dito, em diferentes métodos de aprendizado.

Relembre que dado um conjunto de $n$ observações independentes, $Z_1, ..., Z_n$ , cada uma com variância $\sigma^2$ , a variância da média $\bar{Z}$ será dada por $\frac{\sigma^2}{n}$ .

Ou seja, calcular a média do conjunto de observações reduz a variância.

É imediato pensar que para reduzir a variância e, portanto, aumentar a acurácia da previsão de um determinado método estatístico de aprendizado basta pegarmos muitos conjuntos de treinamento da população, construir um modelo de previsão separado usando cada conjunto, definir e calcular a média das previsões resultantes.

Em outras palavras, nós calculamos $\hat{f}^{1}(x), \hat{f}^{2}(x), ..., \hat{f}^{B}(x)$ usando $B$ conjuntos de treino, calculamos a média deles de modo a obter um único modelo com baixa variância, dado por:

(1) $\begin{align*} \hat{f}_{\text{médio}}(x) = \frac{1}{B} \sum_{b=1}^{B} \hat{f}^{b} (x) \end{align*}$

Isso, infelizmente, não é muito prático já que, em geral, não temos acesso a muitos conjuntos de treino. Assim, o que podemos fazer é aplicar a técnica de bootstrap, de modo a tomar diversas amostras do mesmo conjunto de treino. Assim, geraremos $B$ diferentes conjuntos de treino. A partir daí, podemos treinar nosso método no $b$ conjunto de treino, de modo a obter $\hat{f}^{*b} (x)$ , finalmente obtendo a média das previsões

(2) $\begin{align*} \hat{f}_{\text{bag}}(x) = \frac{1}{B} \sum_{b=1}^{B} \hat{f}^{*b} (x) \end{align*}$

o que chamamos de bagging.

Enquanto o método de bagging pode ser utilizado para aumentar a acurácia da previsão nos métodos de regressão, ele é particularmente útil para árvores de decisão.

Para aplicar o método à árvores de regressão, nós simplesmente construímos $B$ árvores de regressão usando $B$ conjuntos de treino construídos através da aplicação de bagging.

Como as árvores individuais não são podadas, elas crescem bastante, tendo assim alta variância e baixo viés.

Assim, construir a média dessas árvores irá reduzir a variância.

Até aqui, nós descrevemos o método de bagging no contexto de uma regressão, com um variável $Y$ quantitativa. Podemos estender o método para problemas de classificação através de diversas abordagem.

A mais simples é pensar que para um dado conjunto de teste, podemos registrar a classe prevista por cada uma das $B$ árvores e tomamos uma votação majoritária: a previsão que mais ocorre entre as $B$ previsões.

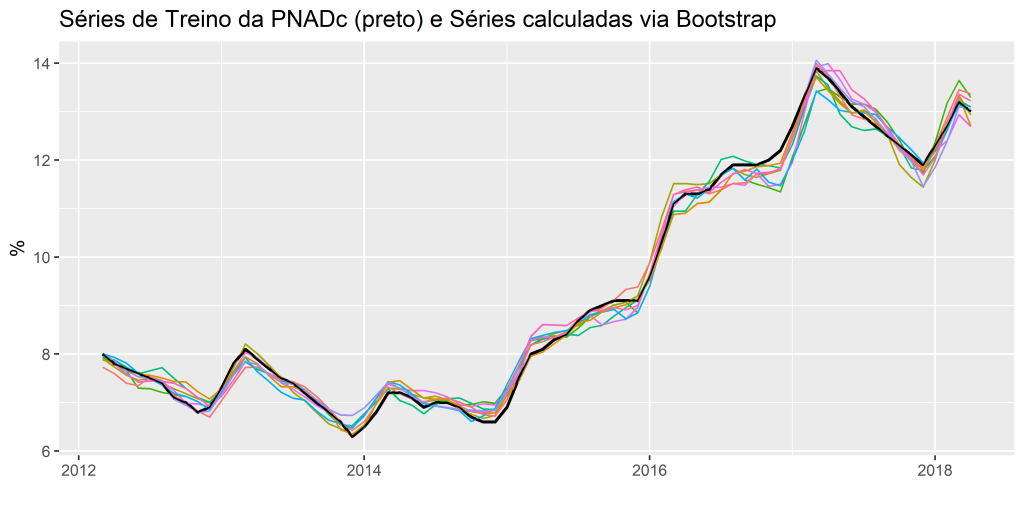
Como exemplo, podemos usar o Desemprego, medido pela PNADC.

Separamos os dados da PNADc em Treino e Teste, e usando o Bootstrap, temos as seguintes séries calculadas, em que na cor preto temos a série de treino e colorido as séries calculadas via Bootstrap:

E com o Auto ARIMA, para gerar as previsões dessas séries, obtemos as seguintes medidas de acurácia para a série original e a série Bagged.

Código

	ME	RMSE	MAE	MPE	MAPE	ACF1	Theil’s U
Test set	-0.652436	0.8046662	0.652436	-5.478551	5.478551	0.8940103	2.925306

Código

	ME	RMSE	MAE	MPE	MAPE	ACF1	Theil’s U
Test set	-0.606604	0.6888099	0.606604	-5.043842	5.043842	0.8024958	2.467657

Random Forest

O método de Random Forest oferece um aprimoramento sobre as arvores construídas pelo método de Bagging por meio de um pequeno ajuste aleatório.

Assim como no método de Bagging, nós construímos um número de árvores de decisão ao fazer o bootstrap do conjunto de treino.

Entretanto, ao construir essas árvores, a cada momento uma divisão na árvore é considerada, uma amostra aleatória de preditores $m$ é escolhida dentro do conjunto completo de preditores $p$ A divisão pode, então, usar apenas um desses $m$ preditores.

Uma nova amostra de $m$ preditores é escolhida a cada divisão, tipicamente $m \approx \sqrt{p}$ . Ou seja, ao construir a nossa floresta, a cada divisão na árvore, o algoritmo não considera o total de preditores disponíveis, mas apenas uma fração deles.

Esse ponto é uma sutileza do método, de modo a descorrelacionar as árvores geradas, considerando a cada divisão apenas um subconjunto dos preditores.

Como é possível notar, a principal diferença entre os métodos de bagging e random forest é a escolha do número de preditores $m$ . Se $m$ for igual a $p$ , temos o método de bagging.^[Um número $m$ baixo será útil quando tivermos preditores muito correlacionados.]

Boosting

Para terminar essa seção, vamos discutir a técnica de Boosting, outra técnica para melhorar a acurácia das previsões resultantes de uma árvore de decisão. Assim como o método de Bagging, ele também pode ser utilizado para diferentes métodos de aprendizado.

A técnica de Boosting é similar a de Bagging, com a exceção de que as árvores aqui crescem de forma sequencial: cada árvore cresce usando informação da árvore que cresceu anteriormente.

O Boosting não envolve aplicar bootstrap sobre o conjunto de treino, ao invés disso cada árvore é ajustada em uma versão modificada do data set original.

Assim como a técnica de Bagging, o método de Boosting envolve combinar um número grande de árvores. Entretanto, ao invés de ajustar uma única árvore sobre os dados, o método de boosting aprende devagar.

Dado um modelo corrente, ajusta-se uma árvore sobre os resíduos do modelo, ao invés da variável resposta Y. Feito isso, nós adicionamos a nova árvore à função de ajuste de modo a atualizar os resíduos.

Cada uma dessas árvores pode ser cada vez menor, com apenas alguns nós, determinado pelo parâmetro $d$ no algoritmo.

Assim, ao ajustar árvores pequenas sobre os resíduos, nós vamos aprimorando $\hat{f}$ em áreas onde ela não performa tão bem.

O parâmetro de encolhimento $\lambda$ reduz o processo ainda mais, permitindo diferentes formatos de árvores.

Como é possível perceber, ao contrário do método de Bagging, o método de Boosting depende fortemente da forma que a árvore já foi construída.

Em resumo, o método de Boosting possui três parâmetros de ajuste:

1. O número de árvores $B$ ;

2. O parâmetro de encolhimento $\lambda$ , que controla a taxa sobre a qual o método aprende, sendo tipicamente notado como 0.01 ou 0.001. Pequenos valores para $\lambda$ dependem de vários altos para $B$ de modo a melhor performance;

3. O parâmetro $d$ de divisões em cada árvore, de modo a controlar a complexidade da amostra gerada.

Referências

James, Gareth; Witten, Daniela; Hastie, Trevor; Tibshirani, Robert. An Introduction to Statistical Learning with Applications in R. Second Edition. Springer

Quer aprender mais?

- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;

- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;

- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Estimando a volatilidade da taxa de câmbio

Como analisar o Núcleo de Inflação no Brasil usando Python?

Propensity Score com Múltiplas Variáveis no R

Análise regional da inflação com dados do IBGE usando Python

Como coletar dados do Banco Central do Chile usando a API com o Python?

Como analisar a relação de risco-retorno de ações?

Outros artigos relacionados

Estimando a volatilidade da taxa de câmbio

O que é Volatilidade? Como podemos calcular essa métrica? Este artigo apresenta uma breve introdução à volatilidade, descreve como podemos calcular a volatilidade utilizando Modelos de Volatilidade Condicional e demonstra a aplicação prática dessa abordagem para estimar a volatilidade da taxa de câmbio BRL/USD por meio da linguagem de programação Python.

Como analisar o Núcleo de Inflação no Brasil usando Python?

O Python se destaca como uma ferramenta robusta para análise de dados, permitindo a aplicação de uma ampla gama de técnicas em dados econômico-financeiros. Neste exercício, destacamos como a linguagem oferece uma facilidade muito grande na coleta de dados dos núcleos do IPCA diretamente do site do Banco Central, na manipulação eficiente desses dados e na construção de gráficos que facilitam a compreensão dos indicadores.

Propensity Score com Múltiplas Variáveis no R

O escore de propensão é provavelmente a maneira mais comum de agregar múltiplas variáveis de correspondência em um único valor que pode ser correspondido, ou seja, muito útil para a realização de pareamento.

O escore de propensão é a probabilidade estimada de que uma determinada observação teria sido tratada. A correspondência de escore de propensão muitas vezes significa selecionar um conjunto de observações de controle correspondidas com valores semelhantes do escore de propensão.