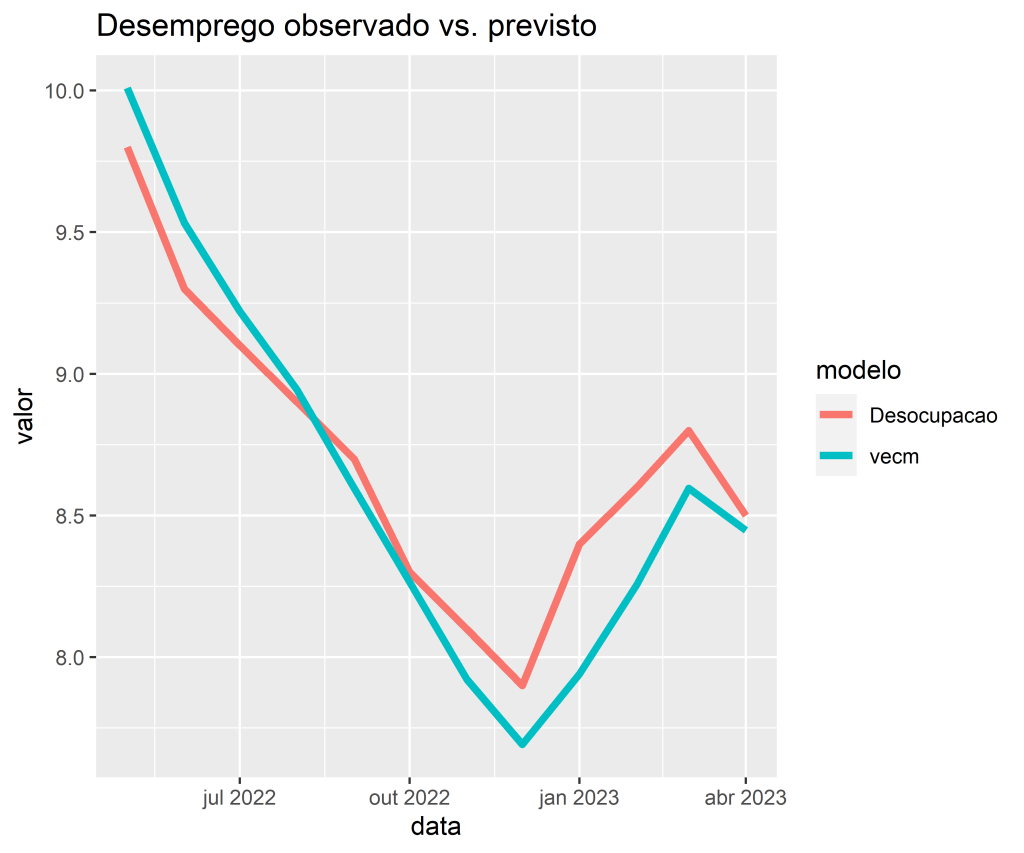
Neste artigo, mostramos como é possível criar uma previsão do Desemprego medida pela PNADc por meio de um VECM utilizando o R e o Python como ferramentas.
O que é Cointegração e VECM?
A cointegração é um conceito estatístico que descreve a relação de longo prazo entre duas ou mais séries temporais. Em muitos casos, as séries temporais podem ser não estacionárias (ou seja, têm uma tendência ou comportamento que muda ao longo do tempo), o que dificulta a análise direta de suas relações. No entanto, a cointegração implica que, mesmo que as séries individuais sejam não estacionárias, pode haver uma combinação linear delas que seja estacionária. Essa combinação linear é chamada de "combinação cointegrada" e representa a relação de equilíbrio de longo prazo entre as séries.
O Modelo de Correção de Erros (ECM) é um tipo de modelo de regressão que é utilizado para estudar a dinâmica de curto prazo entre variáveis cointegradas. Uma vez que as variáveis são cointegradas, elas têm uma relação de longo prazo, mas também podem apresentar movimentos de curto prazo que se desviam do equilíbrio de longo prazo. O ECM é projetado para capturar esses desvios de curto prazo e corrigi-los no próximo período, retornando à relação de equilíbrio de longo prazo.
O Modelo Vetorial de Correção de Erros (VECM) é uma extensão do ECM para casos em que existem mais de duas séries cointegradas. Em outras palavras, é uma generalização do ECM para sistemas com várias variáveis cointegradas. O VECM é especialmente útil quando há um conjunto de variáveis interdependentes que têm uma relação de longo prazo e apresentam ajustamentos de curto prazo uns aos outros.
Para verificar se há cointegração entre duas variáveis, aplicamos o Teste de Engle-Granger.
O teste de cointegração Engle-Granger foi desenvolvida por Robert Engle e Clive Granger para testar a cointegração entre duas séries temporais. Esse teste é adequado quando se tem duas variáveis não estacionárias, mas que podem ser cointegradas. O procedimento é geralmente realizado em duas etapas:
- Etapa 1: Estimar uma regressão de uma variável contra a outra, ou seja, regredir uma das séries na outra. Essa regressão é conhecida como "regressão de cointegração".
- Etapa 2: Verificar a estacionariedade dos resíduos da regressão de cointegração usando testes de raiz unitária, como o teste Augmented Dickey-Fuller (ADF). Se os resíduos forem estacionários, isso sugere a existência de uma relação de longo prazo entre as duas séries, ou seja, elas são cointegradas.
Se o teste de cointegração Engle-Granger rejeitar a hipótese nula de que os resíduos são não estacionários (ou seja, aceita a hipótese alternativa de que eles são estacionários), então conclui-se que há cointegração entre as duas séries.
Para verificar se há cointegração entre duas variáveis ou mais, aplicados o Teste de Johasen.
O teste de cointegração Johansen foi proposto por Søren Johansen. Ao contrário do teste Engle-Granger, o teste de Johansen pode lidar com mais de duas variáveis cointegradas. Ele também permite identificar o número de vetores de cointegração, ou seja, quantas relações de equilíbrio de longo prazo existem entre as variáveis.
O teste de cointegração Johansen é realizado por meio de uma abordagem de vetor de correção de erros (VEC), que é uma extensão do ECM discutido anteriormente. O teste compara diferentes modelos restritos e não restritos para determinar o número de vetores de cointegração. O número de vetores de cointegração indica quantas combinações lineares de longo prazo existem entre as séries.
Estimando um VECM no R e no Python
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
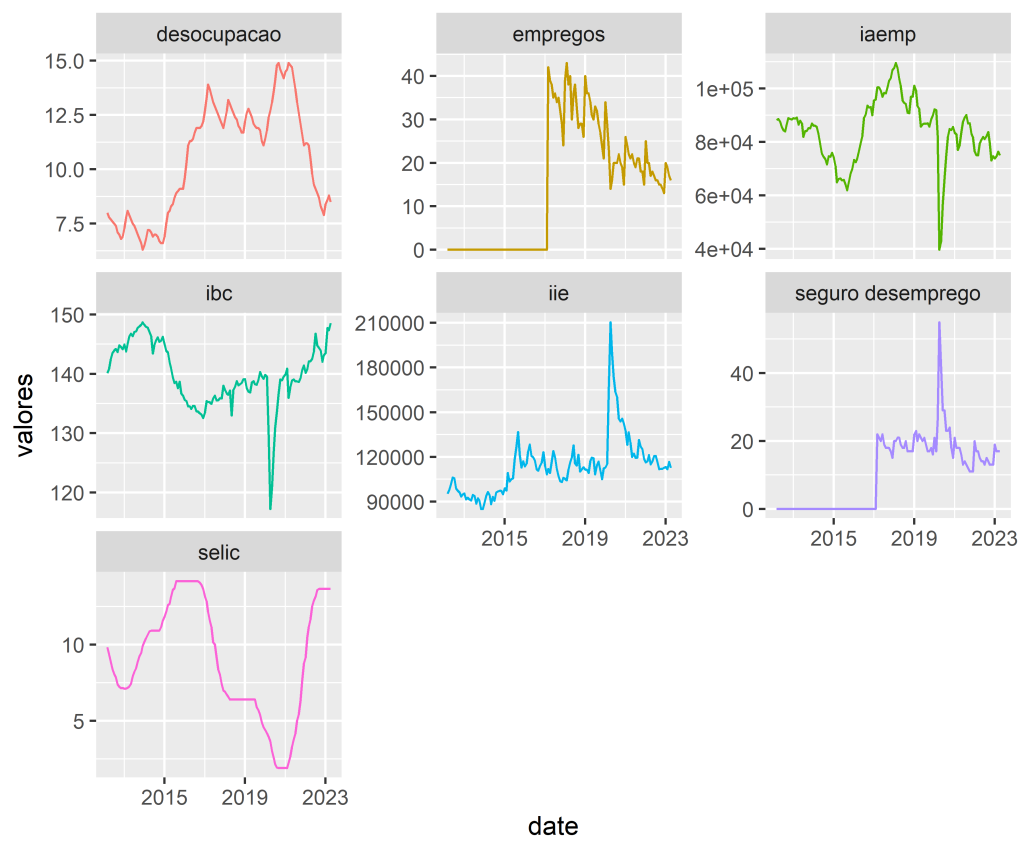
De modo a ilustrar a aplicação do VECM, vamos construir um modelo com foco na trajetória do desemprego. As variáveis utilizadas serão:
- Taxa de desocupação, na semana de referência, das pessoas de 14 anos ou mais de idade (Sidra/IBGE);
- Indicador Antecedente de Emprego (IAEmp) com ajuste sazonal (FGV);
- Indicador de Incerteza da Economia Brasil (IIE-Br) (FGV);
- Termos de busca: “empregos” e “seguro desemprego” (Google);
- Índice de Atividade Econômica do Banco Central (IBC-Br) com ajuste sazonal (BCB);
- Taxa de juros Selic acumulada no mês anualizada base 252 (BCB).
Os dados são importados abaixo:
Podemos aplicar algum teste estatístico para verificar a estacionariedade das séries, entretanto, tomaremos que todas as séries não são estacionárias e prosseguiremos com o teste de Johasen para verificar a cointegração das séries.
Teste de Cointegração e seleção de ordem
Aplicamos o teste com o código abaixo:
Código
Best AIC: rank= 7 lag= 10
Best BIC: rank= 0 lag= 1
Best HQ : rank= 2 lag= 1 Alternativamente, podemos selecionar automaticamente por meio da função ca.jo do pacote urca.
Código
Length Class Mode
1 ca.jo S4 O Teste vai determinar o número de vetores de cointegração ou relações de cointegração (r). O modelo VECM é utilizado quando os vetores de cointegração são maiores que 0 e menores que o número de variáveis no modelo (K).
0 < r < K; aplicar VECM
No nosso exemplo (onde K = 7), a aplicação do VECM é apropriada se o r seja o valor de 2, 3, 4, 5 e 6 pois isso satisfaz a condição acima 0 < r < K (ou seja, 0 < r < 7).
O teste pode ser realizado usando tanto a estatística de Traço (Trace statistic) quanto a estatística do Autovalor Máximo (Maximum Eigenvalue statistic) para testar as seguintes hipóteses:
- Hipótese Nula (H0): Não existe cointegração entre as variáveis (r = 0);
- Hipótese Alternativa (H1): Existe pelo menos uma relação de cointegração entre as variáveis (r > 0).
O teste de cointegração de Johansen avalia se a estatística de teste excede o valor crítico para rejeitar a hipótese nula e inferir a presença de cointegração entre as variáveis.
Não podemos rejeitar a existência de dois vetores de cointegração pelo teste do máximo autovalor.
Ajuste do Modelo
Com efeito, montamos o VECM a seguir.
Código
#############
###Model VECM
#############
Full sample size: 134 End sample size: 132
Number of variables: 7 Number of estimated slope parameters 147
AIC 4300.936 BIC 4753.536 SSR 7167046075
Cointegrating vector (estimated by ML):
desocupacao ibc selic empregos seguro desemprego iaemp
r1 1.000000e+00 0 0.15199253 -0.2097503 0.3252409 -3.553857e-05
r2 2.775558e-17 1 -0.01124626 0.3929251 -0.6308319 1.545753e-04
iie
r1 -0.0001750959
r2 0.0003338637
ECT1 ECT2
Equation desocupacao -0.0431(0.0122)*** -0.0209(0.0042)***
Equation ibc 0.0074(0.1813) -0.2104(0.0630)**
Equation selic -0.0224(0.0242) -0.0002(0.0084)
Equation empregos 1.0800(0.4661)* -0.0319(0.1620)
Equation seguro desemprego 0.1276(0.3583) 0.3737(0.1246)**
Equation iaemp 546.4981(364.6566) -405.9431(126.7905)**
Equation iie 310.6058(732.3435) 153.1594(254.6347)
Intercept
Equation desocupacao 3.4894(0.7496)***
Equation ibc 40.2513(11.1640)***
Equation selic -0.1679(1.4909)
Equation empregos 16.5253(28.6966)
Equation seguro desemprego -69.6565(22.0597)**
Equation iaemp 83851.5817(22453.3003)***
Equation iie -25403.0418(45093.1876)
desocupacao -1 ibc -1
Equation desocupacao 0.5332(0.0676)*** -0.0099(0.0090)
Equation ibc -0.7163(1.0065) 0.3882(0.1335)**
Equation selic -0.1619(0.1344) 0.0055(0.0178)
Equation empregos 3.2843(2.5872) 0.4857(0.3432)
Equation seguro desemprego 2.2159(1.9888) -0.6126(0.2638)*
Equation iaemp 1962.2871(2024.3281) 1124.7394(268.5401)***
Equation iie -4784.1888(4065.4784) -1356.8961(539.3118)*
selic -1 empregos -1
Equation desocupacao -0.0664(0.0304)* -0.0022(0.0035)
Equation ibc 0.2521(0.4520) -0.0038(0.0524)
Equation selic 0.7662(0.0604)*** -0.0062(0.0070)
Equation empregos -0.1062(1.1619) -0.1383(0.1347)
Equation seguro desemprego -0.5632(0.8932) -0.0897(0.1035)
Equation iaemp 418.1077(909.0962) 141.7615(105.3623)
Equation iie -1323.7460(1825.7470) -107.1595(211.6001)
seguro desemprego -1 iaemp -1
Equation desocupacao -0.0054(0.0055) 7.0e-06(3.7e-06).
Equation ibc 0.0369(0.0818) -6.9e-05(5.6e-05)
Equation selic 0.0097(0.0109) 9.7e-06(7.4e-06)
Equation empregos 0.0032(0.2104) -0.0001(0.0001)
Equation seguro desemprego -0.0551(0.1617) 0.0003(0.0001)**
Equation iaemp -109.6563(164.6007) -0.3098(0.1120)**
Equation iie -108.9532(330.5693) 0.8136(0.2249)***
iie -1 Jan
Equation desocupacao 2.9e-06(2.4e-06) 0.4395(0.0525)***
Equation ibc -5.7e-05(3.5e-05) -0.4359(0.7821)
Equation selic -2.8e-06(4.7e-06) -0.1275(0.1044)
Equation empregos -2.2e-06(9.1e-05) 7.6255(2.0103)***
Equation seguro desemprego 0.0002(7.0e-05)* 3.2627(1.5454)*
Equation iaemp -0.2204(0.0709)** 122.3226(1572.9471)
Equation iie 0.4058(0.1424)** -2612.0281(3158.9654)
Feb Mar
Equation desocupacao 0.2483(0.0651)*** 0.2484(0.0689)***
Equation ibc 0.2573(0.9697) -1.4734(1.0255)
Equation selic 0.1371(0.1295) 0.0234(0.1370)
Equation empregos -0.4588(2.4925) 1.1885(2.6360)
Equation seguro desemprego -1.1602(1.9160) 2.0844(2.0263)
Equation iaemp -2585.1165(1950.2101) -4642.7594(2062.4725)*
Equation iie 925.6537(3916.6264) 11571.3462(4142.0842)**
Apr May
Equation desocupacao -0.2874(0.0700)*** -0.0606(0.0530)
Equation ibc 0.1378(1.0425) -0.3835(0.7891)
Equation selic 0.0591(0.1392) 0.0489(0.1054)
Equation empregos -0.8513(2.6798) -0.2913(2.0283)
Equation seguro desemprego 0.1078(2.0600) -0.7021(1.5592)
Equation iaemp -2484.0205(2096.7682) -950.4413(1587.0401)
Equation iie 1001.1409(4210.9606) -2247.8865(3187.2685)
Jun Jul
Equation desocupacao -0.0944(0.0521). 0.0479(0.0529)
Equation ibc -0.0713(0.7753) 0.4035(0.7883)
Equation selic -0.0909(0.1035) -0.0296(0.1053)
Equation empregos 1.0736(1.9929) 2.3437(2.0264)
Equation seguro desemprego -0.0009(1.5320) 0.1741(1.5577)
Equation iaemp -1942.4743(1559.2942) 254.0573(1585.5242)
Equation iie 1966.7025(3131.5462) -4092.8244(3184.2241)
Aug Sep
Equation desocupacao 0.0002(0.0531) -0.1112(0.0524)*
Equation ibc -0.4155(0.7909) 0.0136(0.7799)
Equation selic -0.0549(0.1056) -0.1135(0.1042)
Equation empregos 0.7303(2.0329) 0.8789(2.0046)
Equation seguro desemprego 0.0933(1.5628) -0.7132(1.5410)
Equation iaemp -898.1784(1590.6336) 1.4621(1568.5062)
Equation iie -227.6257(3194.4855) 151.6437(3150.0468)
Oct Nov
Equation desocupacao -0.0996(0.0519). -0.0672(0.0520)
Equation ibc 0.5365(0.7733) -0.9488(0.7743)
Equation selic -0.0024(0.1033) -0.0649(0.1034)
Equation empregos 1.3635(1.9879) 0.7106(1.9903)
Equation seguro desemprego -0.4163(1.5281) 0.4063(1.5300)
Equation iaemp 1166.8437(1555.3768) -1371.5672(1557.2902)
Equation iie -5597.5582(3123.6788). -1481.5278(3127.5216) Realizamos uma análise exploratória dos coeficientes estimados para cada equação.
Código
| .model | n_coeficientes | n_significativos | perc_significativos |
|---|---|---|---|
| vecm | 147 | 32 | 21.76871 |
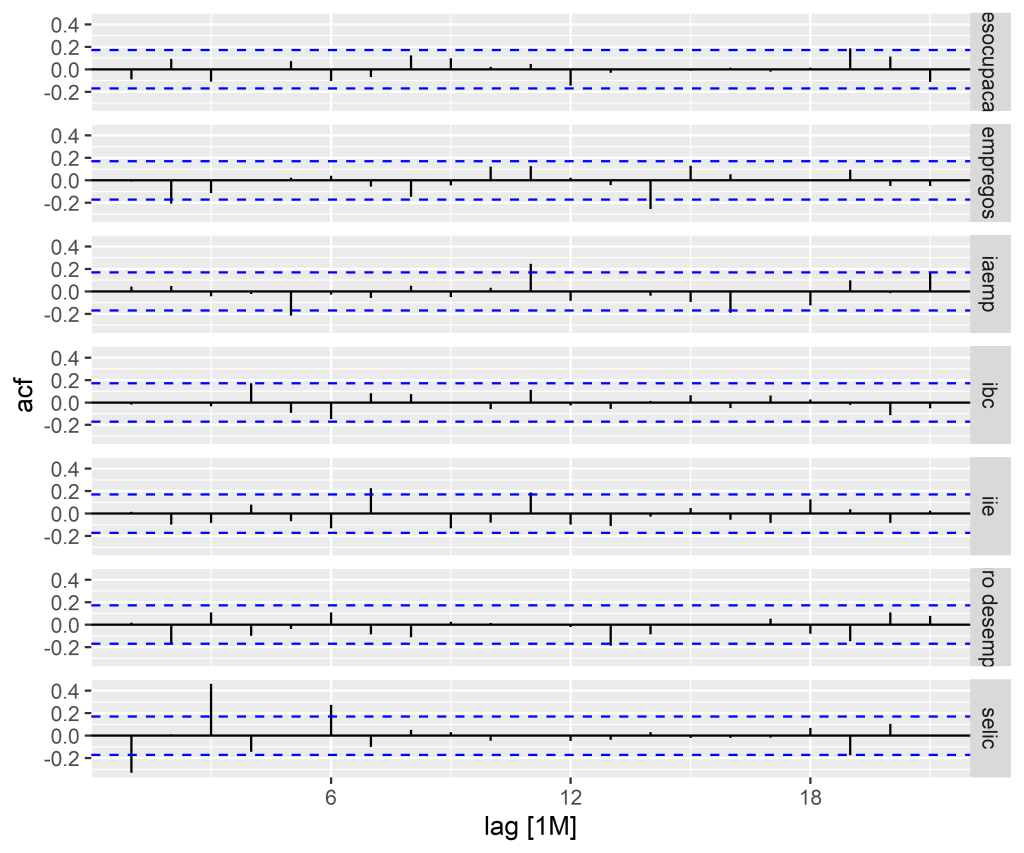
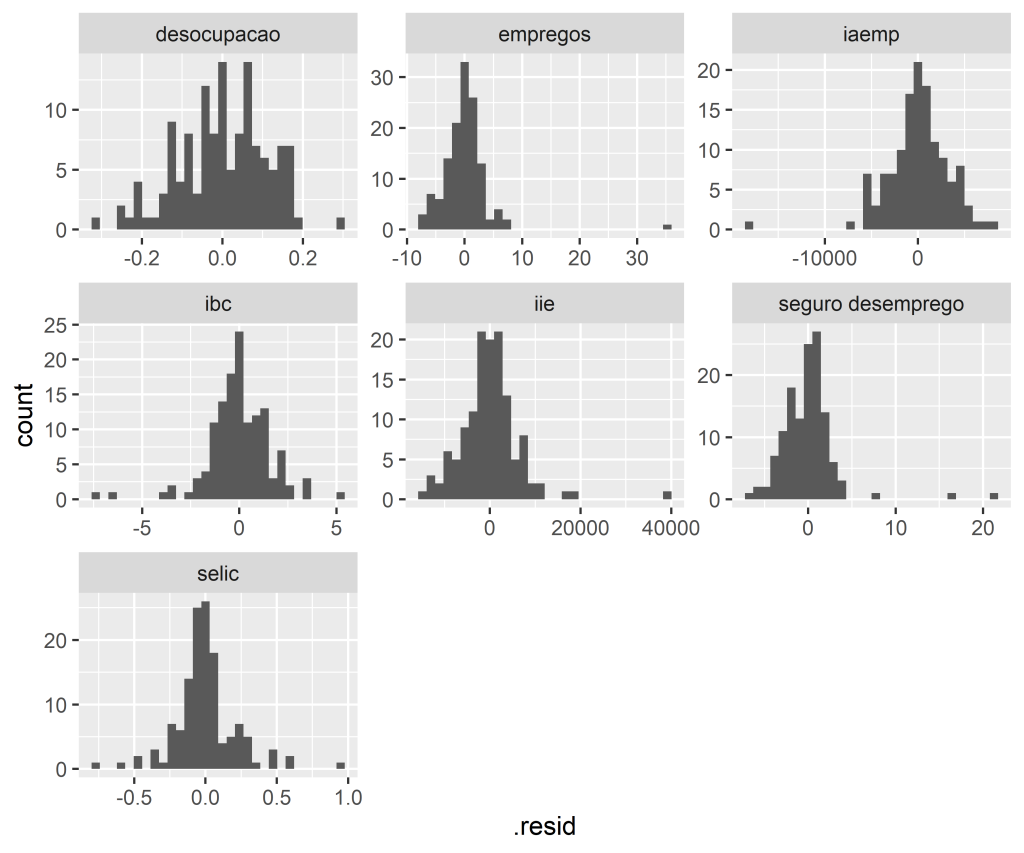
Avaliação do Modelo
Realizamos o diagnóstico dos resíduos:
Previsões
Separação de treino e teste
Fazemos a separação dos dados em treino e teste, selecionando as 12 últimas observações do dataset para teste, com o objetivo de comparar com previsões realizadas pelo modelo e compreender o quão bom é o ajuste.
Previsão dentro da amostra
Acurácia
Código
ME RMSE MAE MPE MAPE
desocupacao 8.150755e-02 0.2186051 0.1823663 1.032638 2.106286
ibc 3.142117e+00 4.2036241 3.1778005 2.142145 2.167262
selic -5.884785e-01 0.9008741 0.6896675 -4.287509 5.076198
empregos 6.096583e+00 6.4356425 6.0965827 37.778494 37.778494
seguro desemprego 1.687319e+00 2.6469115 2.1027094 10.665031 13.551108
iaemp 7.640003e+03 8488.4136210 7640.0025468 9.675761 9.675761
iie -7.581552e+03 8967.3181771 7581.5522831 -6.671798 6.671798
global 9.838473e+00 4666.9970162 2176.2577081 7.190680 11.003844U-Theil: 0.7496841
Previsão Fora da Amostra
___________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.
