O Spread Bancário é definido como a diferença entre o custo do empréstimo e a remuneração oferecida ao poupador. Neste exercício, propomos a elaboração de um modelo para analisar o Spread Bancário no contexto brasileiro, empregando uma abordagem de regressão linear múltipla. Para realizar essa análise, utilizamos a linguagem de programação Python como ferramenta principal.
O spread bancário é a diferença entre a taxa de captação dos bancos e a taxa de empréstimo ao tomador de crédito. Ele é diretamente influenciado pelas condições macroeconômicas, em especial às flutuações na taxa básica de juros, mas não apenas a ela.
Há inúmeros fatores que definem o spread cobrado pelos bancos, conforme a definição estabelecida pelo Banco Central, em particular:
- Custo do depósito compulsório
- Impostos
- Despesas administrativas e judiciais
- Inadimplência
- Lucros dos bancos
Sendo assim temos os fatores que influenciam o spread determinados pelos Bancos e fatores que não são determinados pelos Bancos.
Com o objetivo de Modelar o Spread Bancário no Brasil propomos um modelo que vise captar algumas determinantes do Spread, mas não todas, visto a dificuldade de obter determinadas variáveis.
Aprenda a coletar, processar, analisar e modelar dados macroeconômicos no curso de Macroeconometria usando o Python.
Como variáveis explicativas para o spread bancário, foram utilizadas:
- provisões dos bancos
- compulsórios bancários
- taxa de inadimplência
- taxa básica de juros
- taxa de desemprego
As variáveis são transformadas na pela diferença com o objetivo de evitar problemas na estimação dos parâmetros da regressão linear múltipla. No modelo, verificamos que compulsórios e provisões não foram significativos.
Análise dos Dados
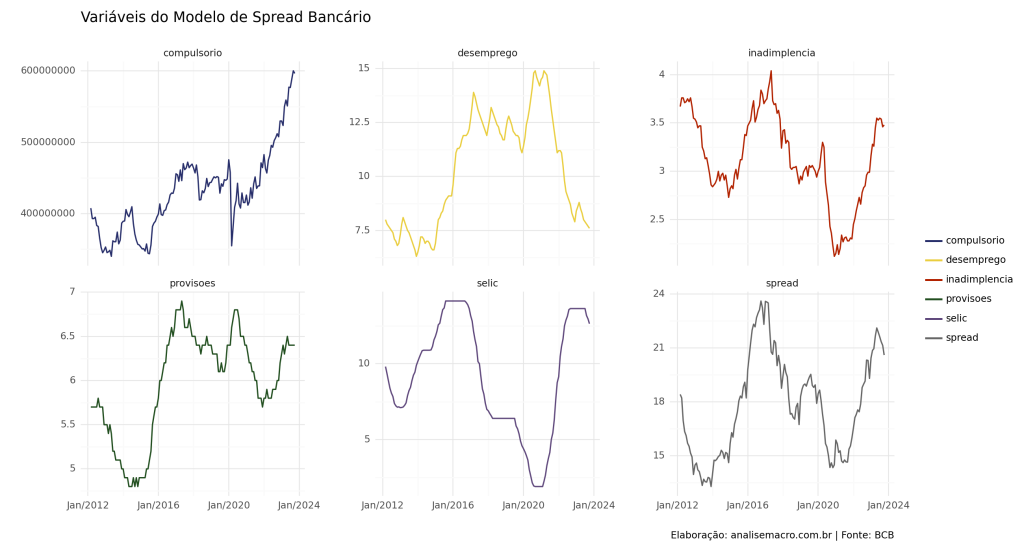
Verificamos as possíveis variáveis utilizadas no modelos através dos gráficos abaixo. Vemos que de fato há correlação entre algumas variáveis em relação ao Spread bancário, principalmente a Selic, Inadimplência e Desemprego.
Modelo
Dada as circunstâncias das séries temporais em mãos, aplicamos a diferenciação nos mesmos com o objetivo de evitar problemas de viés na estimação dos parâmetros usando o MQO. Além disso, após diferentes testes, construímos o melhor modelo possível como apresentado na tabela abaixo, em que o spread é função da variação da inadimplência e sua primeira defasagem, da variação interanual da selic e da variação em p.p. do desemprego e sua defasagem.
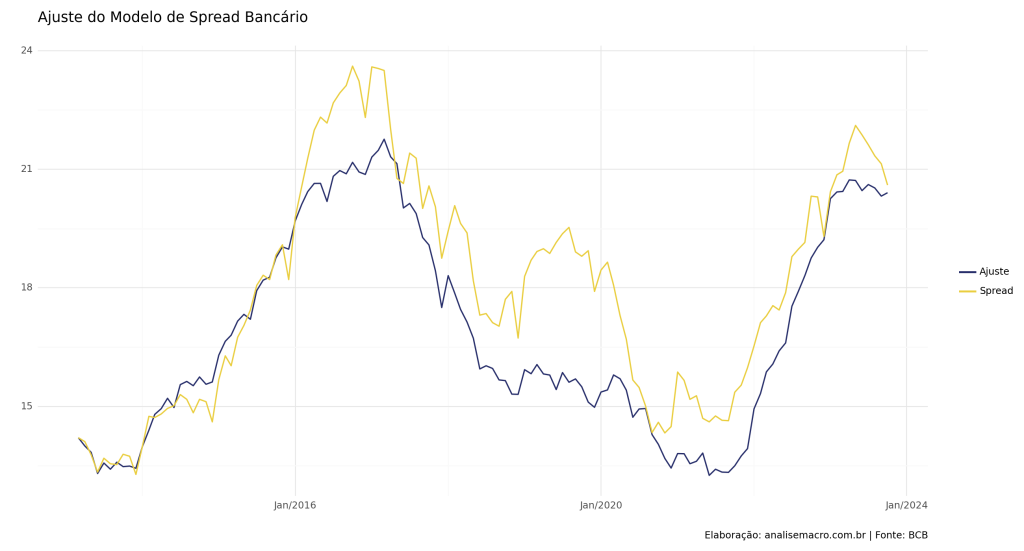
Com o modelo criado, podemos realizar uma comparação entre o ajuste e os dados reais do Spread, verificando descolamento em determinados períodos, também evidenciado pelo valor do R² de 40%.
Código
| Dep. Variable: | spread.diff() | R-squared: | 0.403 |
| Model: | OLS | Adj. R-squared: | 0.378 |
| Method: | Least Squares | F-statistic: | 16.46 |
| Date: | Thu, 25 Jan 2024 | Prob (F-statistic): | 2.15e-12 |
| Time: | 15:05:36 | Log-Likelihood: | -82.389 |
| No. Observations: | 128 | AIC: | 176.8 |
| Df Residuals: | 122 | BIC: | 193.9 |
| Df Model: | 5 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 0.0188 | 0.042 | 0.444 | 0.658 | -0.065 | 0.103 |
| inadimplencia.diff() | 2.0949 | 0.455 | 4.608 | 0.000 | 1.195 | 2.995 |
| inadimplencia.shift(1).diff() | -1.4512 | 0.454 | -3.196 | 0.002 | -2.350 | -0.552 |
| selic.diff(12) | 0.0577 | 0.014 | 4.209 | 0.000 | 0.031 | 0.085 |
| desemprego.diff() | 0.6717 | 0.185 | 3.621 | 0.000 | 0.305 | 1.039 |
| desemprego.shift(1).diff() | -0.3425 | 0.190 | -1.804 | 0.074 | -0.718 | 0.033 |
| Omnibus: | 1.658 | Durbin-Watson: | 2.120 |
| Prob(Omnibus): | 0.436 | Jarque-Bera (JB): | 1.255 |
| Skew: | -0.227 | Prob(JB): | 0.534 |
| Kurtosis: | 3.172 | Cond. No. | 41.2 |
Análise dos Resíduos
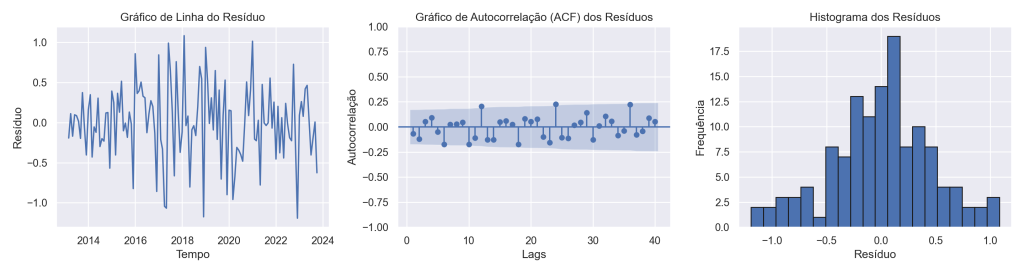
Por fim, analisamos os resíduos do modelo, em que há, por suposto, estacionariedade e ausência de autocorrelação. O Histograma demonstra uma quase simetria.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.