O termo "Regra de Bolso" pode ser entendido como um regra prática, basicamente um método aproximado para fazer algo, baseado na experiência prática. A Regra de Taylor propõe-se a ser utilizada com este intuito, visando determinar a taxa de juros básica da economia, usando um subconjunto da informação necessária para uma regra ótima do instrumento de política monetária. Neste artigo, veremos como podemos criar a Regra de Taylor facilmente usando o Python, tomando como base dados da economia brasileira.
A Regra de Taylor, também conhecida como Regra da Taxa de Juros de Taylor, é uma fórmula usada para prever a taxa de juros de um banco central com base em vários fatores econômicos. Portanto, é uma ferramenta muito importante para a tomada de decisões da autoridade monetária.
A regra é simples, no sentido de que não necessita de muitas informações, diferente de uma regra ótima para a instrumentalização da política monetária, que necessita de diversas informações e modelos muito bem calibrados.
Nessa regra simples os coeficientes são ad hoc, baseados na experiência e qualificação do banco central, de forma que não refletem comportamentos tidos como ótimos.
Criada pelo Economista John B. Taylor, a regra relaciona a taxa de juros determinada pelo banco central com as condições econômicas, especificamente os desvios da inflação e a meta de inflação e o hiato entre o produto real e produto potencial.
A diferença da regra ótima, na regra de Taylor o instrumento de política depende de variáveis endógenas e a regra de Taylor não é solução de um problema de política monetária. Este aspecto deve ser levado em conta ao fazer a estimação empírica da regra. A regra de Taylor pode ser tratada como uma regra com realimentação (feedback rule).
Aprenda a coletar, processar, analisar e modelar dados macroeconômicos no curso de Macroeconometria usando o Python.
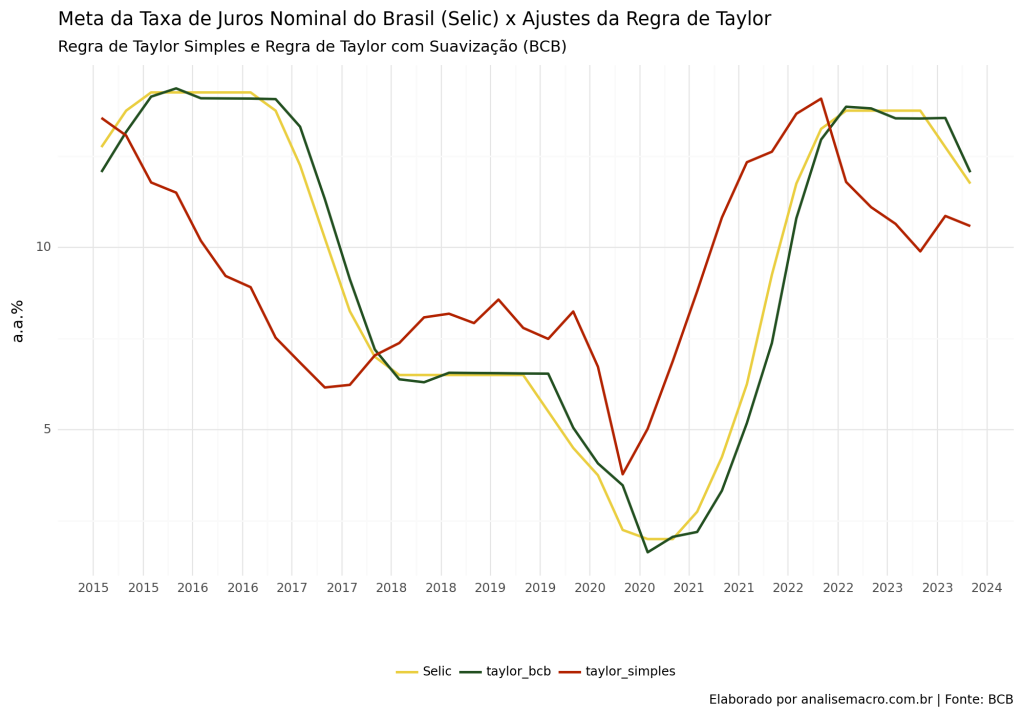
A regra proposta nos moldes por Taylor sofreu diversas alterações ao longo do tempo, diferenciando-se em diversas formas e aspectos, para diferentes finalidades. No presente artigo, iremos analisar duas formas: uma regra simples, nos moldes originais propostos por Taylor; e uma regra que leva em consideração termos de suavização com um componente autoregressivo da taxa de juros, além disso, há a adição de um termo de juro real neutro variante no tempo:
Temos então a primeira equação:
![\[i_t = \alpha_0 + \alpha_1 (\pi_{t} - \pi_{t}^{M}) + \alpha_2 h_{t-1} + \epsilon_t\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-7a52580614659df7f5e9c76205aa02ff_l3.png "Rendered by QuickLaTeX.com")
Em que 
representa a meta da taxa de juros nominal, 
os desvios da inflação em relação a meta, 
o hiato do produto (diferença entre o produto real e produto potencial), por fim, temos 
representando os choques. Aqui a constante 
representa o taxa de juro neutra invariante no tempo.
A segunda equação estabelece mais estrutura para a regra:
![\[i_t=\theta_1 i_{t-1}+\theta_2 i_{t-2}+\left(1-\theta_1-\theta_2\right) *\left[r_t^{e q}+\pi_t^{\text {meta }}+\theta_3\left(\pi_{t}-\pi_t^{\text {meta }}\right)\right]+\epsilon_t^i\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-08c17ff48f7371a1fbe95da4f3eed094_l3.png "Rendered by QuickLaTeX.com")
Em que 
representa a taxa de juros real neutra variante no tempo. 
e 
referem-se a coeficientes que visam ser uma suavização para o tempo de resposta da diretoria do banco central, bem como prevenir autocorrelação nos resíduos. Importante dizer que para garantir a convergência desses termos autoregressivos é necessário que a soma dos termos seja inferior a 1.
Os dados utilizados referem-se:
- Taxa de juros - Meta Selic definida pelo Copom - Freq. diária - Unid. % a.a.
- Índice nacional de preços ao consumidor-amplo (IPCA) Var. % mensal
- Meta para a inflação - CMN - Freq. anual - %
- Hiato do Produto criado pelo BCB, obtido pelo Relatório de Inflação.
- Juro Neutro: Expectativa da taxa Selic ao longo de uma horizonte de quatro anos à frente, desinflacionada pela expectativa de variação do IPCA para o mesmo período, ambas obtidas pela pesquisa Focus. Do resultado, aplica-se o Filtro HP para suavizar a série.
O coeficientes são estimados via OLS. Os dados que não se referem a frequência trimestral são transformados para a utilização do modelo.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
