Introdução
Inércia ou persistência não são exclusivas do processo inflacionário. Em termos econométricos, a maioria das variáveis macroeconômicas exibe algum grau de persistência, evidenciado por uma autorregressividade positiva. Em outras palavras, se uma variável macroeconômica puder ser descrita por um processo autorregressivo de primeira ordem, como em:
onde , diz-se que a variável apresenta persistência. O grau de persistência é crucial. No estudo de séries temporais, sabemos que, se
estiver no intervalo aberto entre 0 e 1, o processo autorregressivo é considerado estacionário.
Nesse caso, mesmo que a persistência seja alta (isto é, esteja próximo de 1), choques de oferta terão efeito temporário, dissipando-se com o tempo. Entretanto, se
for maior ou igual a 1, a série deixa de ser estacionária, o que implica um desvio permanente em resposta a choques na variável.
Assim, faz sentido interpretar o coeficiente como uma medida de persistência para qualquer variável macroeconômica, ou de inércia, no caso específico da inflação.
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Modelo
Para construir um modelo que capture a inércia inflacionária em uma estrutura de espaço de estados, onde:
- representa o Índice de Preços ao Consumidor Amplo (IPCA) do período atual, e
- representa o IPCA defasado (IPCA do período anterior),
configuramos o modelo de modo que o coeficiente de inércia inflacionária seja representado por um termo variável no tempo, , que responde a variações ao longo do tempo.
Quer saber como construir modelos macroeconômicos? Veja nosso curso de Macroeconometria usando Python.
Estrutura do Modelo de Espaço de Estados
1. Equação de Observação
A equação de observação modela a relação entre o IPCA atual () e o IPCA defasado (
) através do coeficiente
, que representa a inércia inflacionária:
onde:
- é o termo de erro do modelo, assumido como ruído branco (distribuído normalmente com média zero e variância
).
2. Equação de Estado
A equação de estado descreve a evolução de ao longo do tempo, assumindo que ele segue uma caminhada aleatória, permitindo capturar mudanças na inércia inflacionária:
onde:
- é o ruído de estado, também assumido como ruído branco com média zero e variância
, permitindo que
varie de forma gradual, sem uma tendência fixa.
Implementação em Python com statsmodels
Com base no exemplo fornecido pelo módulo statespace do statsmodels, podemos acessar módulos e funções pré-definidas para a construção de modelos, como SARIMAX, VAR, Componentes Não Observados e Modelos de Fatores Dinâmicos. Além disso, podemos criar modelos customizados usando programação orientada a objetos no Python, o que permite construir o modelo para o coeficiente de inércia inflacionária. Abaixo está uma implementação simplificada em Python utilizando o statsmodels.
Código
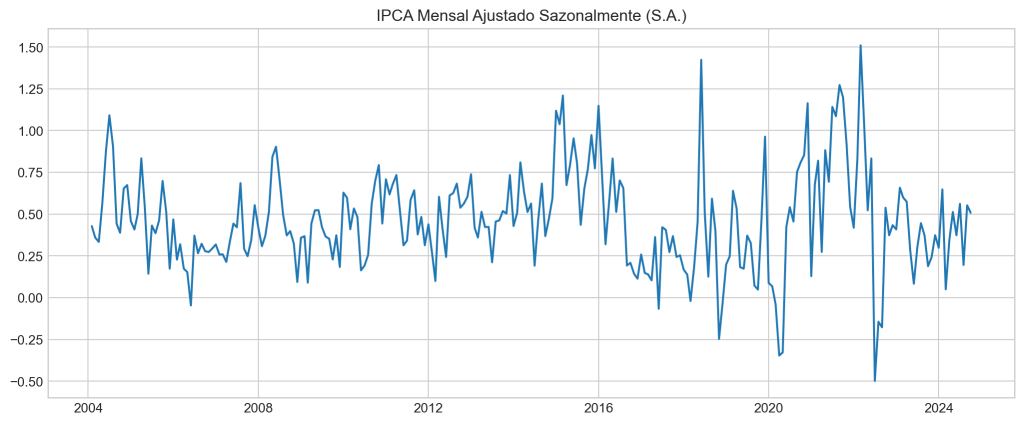
- Coleta de dados: Primeiramente, capturamos a série temporal para a variação mensal do IPCA através do Banco Central. Ajustamos sazonalmente a série utilizando uma decomposição clássica aditiva e criamos o preditor, IPCA defasado.
- Classe
TVRegressionInflacao: Esta classe define um modelo customizado usandostatsmodels, que herda deMLEModel. Este modelo:- Define a equação de observação com um design que varia ao longo do tempo.
- Configura a equação de estado como uma caminhada aleatória para
.
- Permite que as variâncias sejam estimadas como parâmetros e aplica uma transformação para garantir que sejam positivas.
- Ajuste e Resultados: Após ajustar o modelo aos dados, visualizamos a estimativa suavizada de
ao longo do tempo, comparando-a com o valor constante de
estimado via MQO tradicional.
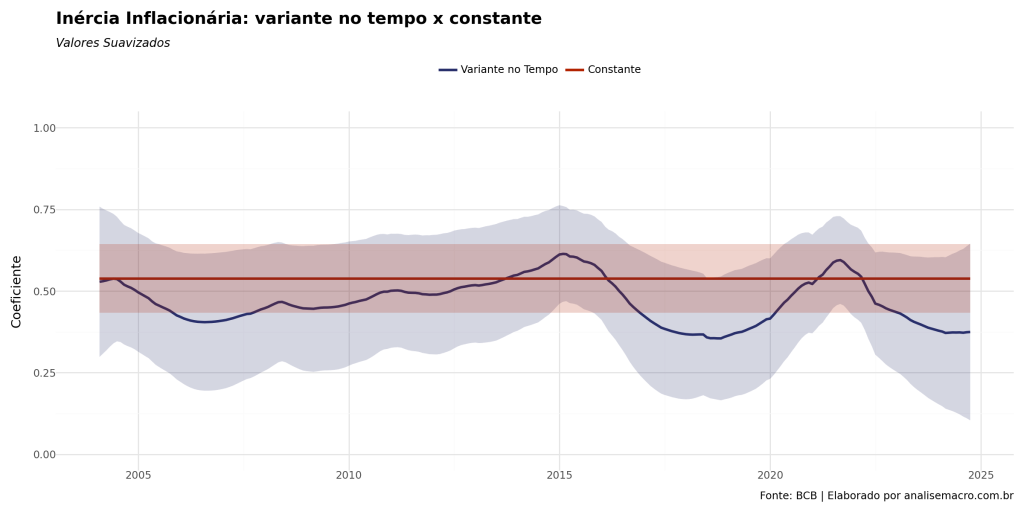
Interpretação
O gráfico final mostra a inércia inflacionária estimada ao longo do tempo, permitindo observar como (a inércia inflacionária) se ajusta às mudanças dinâmicas na relação entre o IPCA atual e o IPCA defasado.
Este modelo é útil em economia para capturar efeitos de inércia não constantes, refletindo mudanças estruturais no comportamento inflacionário ao longo do tempo.
Resultados
Código
Statespace Model Results
==============================================================================
Dep. Variable: ipca_sa No. Observations: 249
Model: TVRegression Log Likelihood -13.006
Date: Wed, 13 Nov 2024 AIC 34.012
Time: 11:18:04 BIC 48.082
Sample: 02-01-2004 HQIC 39.676
- 10-01-2024
Covariance Type: opg
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
intercept 0.2344 0.031 7.598 0.000 0.174 0.295
var.e 0.0599 0.004 16.762 0.000 0.053 0.067
var.x.coeff 0.0011 0.001 1.527 0.127 -0.000 0.003
===================================================================================
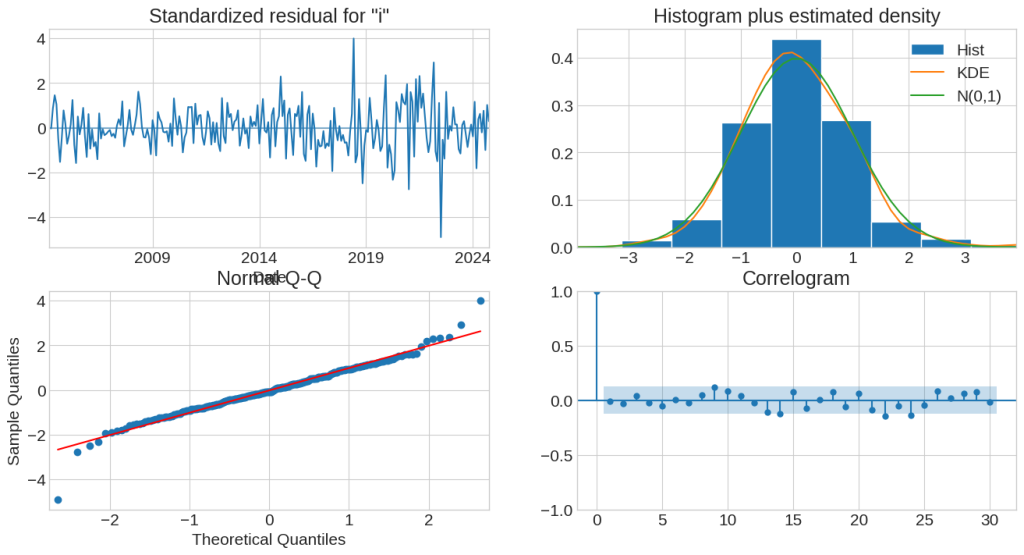
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 72.24
Prob(Q): 0.90 Prob(JB): 0.00
Heteroskedasticity (H): 3.62 Skew: -0.14
Prob(H) (two-sided): 0.00 Kurtosis: 5.63
===================================================================================Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Diagnóstico
 Visualização
Visualização
Referências
FULTON, Chad. Estimating time series models by state space methods in Python: Statsmodels. 2017. Disponível em: https://www.chadfulton.com/files/fulton_statsmodels_2017_v1.pdf. Acesso em: 13/11/2024.
STATS MODELS. Custom statespace models. Disponível em: https://www.statsmodels.org/dev/examples/notebooks/generated/statespace_custom_models.html#Model-1:-time-varying-coefficients. Acesso em: 13/11/2024.
LERIPIO, J. Renato. R for Economic Research: Essential tools for modern economic analysis. 2023. Capítulo 12. Disponível em: https://book.rleripio.com/. Acesso em: 13/11/2024.
Tenha acesso ao código e suporte desse e de mais 500 exercícios no Clube AM!
Quer o código desse e de mais de 500 exercícios de análise de dados com ideias validadas por nossos especialistas em problemas reais de análise de dados do seu dia a dia? Além de acesso a vídeos, materiais extras e todo o suporte necessário para você reproduzir esses exercícios? Então, conheça o Clube AM clicando aqui.